Objectivos de aprendizagem
No final desta secção, será capaz de:
- Definir forças não-conservadoras e explicar como estas afectam a energia mecânica.
- Mostrar como o princípio da conservação de energia pode ser aplicado tratando as forças conservadoras em termos das suas energias potenciais e quaisquer forças não conservadoras em termos do trabalho que fazem.
Forças não conservadoras e Fricção
Forças são conservadoras ou não conservadoras. As forças conservadoras foram discutidas nas Forças Conservadoras e na Energia Potencial. Uma força não-conservadora é aquela para a qual o trabalho depende do caminho tomado. O atrito é um bom exemplo de uma força não-conservadora. Como ilustrado na Figura 1, o trabalho realizado contra o atrito depende da extensão do caminho entre o ponto de partida e o ponto de chegada. Devido a esta dependência do caminho, não existe energia potencial associada a forças não-conservadoras. Uma característica importante é que o trabalho realizado por uma força não-conservadora adiciona ou remove energia mecânica de um sistema. A fricção, por exemplo, cria energia térmica que se dissipa, removendo energia do sistema. Além disso, mesmo que a energia térmica seja retida ou capturada, não pode ser totalmente convertida de volta ao trabalho, pelo que se perde ou não é recuperável também nesse sentido.

Figure 1. A quantidade do rosto feliz apagado depende do caminho percorrido pelo apagador entre os pontos A e B, tal como o trabalho feito contra o atrito. É feito menos trabalho e é apagado menos do rosto para o caminho em (a) do que para o caminho em (b). A força aqui é o atrito, e a maior parte do trabalho vai para a energia térmica que posteriormente deixa o sistema (a cara feliz mais o apagador). A energia gasta não pode ser totalmente recuperada.
Como as forças não-conservadoras afectam a energia mecânica
A energia mecânica não pode ser conservada quando forças não-conservadoras actuam. Por exemplo, quando um carro é parado por fricção em terreno plano, perde energia cinética, que é dissipada como energia térmica, reduzindo a sua energia mecânica. A figura 2 compara os efeitos das forças conservadoras e não conservadoras. Escolhemos frequentemente compreender sistemas mais simples como o descrito na Figura 2a primeiro antes de estudar sistemas mais complicados como na Figura 2b.

Figure 2. Comparação dos efeitos de forças conservadoras e não conservadoras sobre a energia mecânica de um sistema. (a) Um sistema com apenas forças conservadoras. Quando uma rocha é lançada sobre uma mola, a sua energia mecânica permanece constante (negligenciando a resistência do ar) porque a força na mola é conservadora. A mola pode impulsionar a rocha de volta à sua altura original, onde mais uma vez tem apenas energia potencial devido à gravidade. (b) Um sistema com forças não conservadoras. Quando a mesma rocha é lançada ao solo, é parada por forças não conservadoras que dissipam a sua energia mecânica como energia térmica, som, e distorção da superfície. A rocha perdeu energia mecânica.
Como se aplica o teorema Trabalho-Energia
Agora vamos considerar qual a forma que o teorema trabalho-energia assume quando tanto forças conservadoras como não conservadoras actuam. Veremos que o trabalho realizado pelas forças não-conservadoras equivale à mudança na energia mecânica de um sistema. Como foi observado no Teorema Energia Cinética e o Teorema Trabalho-Energia, o teorema trabalho-energia afirma que o trabalho em rede num sistema é igual à mudança na sua energia cinética, ou Wnet = ΔKE. O trabalho em rede é a soma do trabalho das forças não-conservadoras mais o trabalho das forças conservadoras. Isto é,
Wnet = Wnc + Wc,
so que
Wnc + Wc = ΔKE,
onde Wnc é o trabalho total feito por todas as forças não-conservadoras e Wc é o trabalho total feito por todas as forças conservadoras.

Figure 3. Uma pessoa empurra um caixote para cima de uma rampa, fazendo trabalho no caixote. A fricção e a força gravitacional (não mostrada) também fazem trabalho no caixote; ambas as forças se opõem ao empurrão da pessoa. medida que a caixa é empurrada para cima da rampa, ganha energia mecânica, implicando que o trabalho feito pela pessoa é maior do que o trabalho feito por fricção.
Figura 3, na qual uma pessoa empurra uma caixa para cima de uma rampa e é oposta por fricção. Como na secção anterior, notamos que o trabalho realizado por uma força conservadora provém de uma perda de energia potencial gravitacional, de modo que Wc = -ΔPE. A substituição desta equação na anterior e a resolução para Wnc dá
Wnc = ΔKE + ΔPE.
Esta equação significa que a energia mecânica total (KE + PE) muda exactamente pela quantidade de trabalho realizado por forças não conservadoras. Na Figura 3, este é o trabalho realizado pela pessoa menos o trabalho realizado por fricção. Assim, mesmo que a energia não seja conservada para o sistema de interesse (como a caixa), sabemos que uma quantidade igual de trabalho foi feito para causar a mudança na energia mecânica total.
Reorganizamos Wnc = ΔKE + ΔPE para obter
KEi + PEi + Wnc = KEf + PEf.
Isto significa que a quantidade de trabalho feito por forças não-conservadoras adiciona à energia mecânica de um sistema. Se Wnc for positivo, então a energia mecânica é aumentada, tal como quando a pessoa empurra o caixote para cima da rampa na Figura 3. Se Wnc for negativo, então a energia mecânica é diminuída, tal como quando a rocha atinge o solo na Figura 2b. Se Wnc é zero, então a energia mecânica é conservada, e as forças não-conservadoras são equilibradas. Por exemplo, quando se empurra um cortador de relva a uma velocidade constante em terreno plano, o trabalho feito é removido pelo trabalho de fricção, e o cortador de relva tem uma energia constante.
Aplicando Conservação de Energia com Forças Não-Conservadoras
Quando não ocorre nenhuma alteração na energia potencial, aplicar KEi + PEi + Wnc = KEf + PEf equivale a aplicar o teorema trabalho-energia definindo a alteração da energia cinética como sendo igual ao trabalho líquido feito no sistema, o que no caso mais geral inclui tanto forças conservadoras como não conservadoras. Mas quando se procura em vez disso encontrar uma mudança na energia mecânica total em situações que envolvem mudanças tanto na energia potencial como na energia cinética, a equação anterior KE i + PEi + Wnc = KEf + PEf diz que se pode começar por encontrar a mudança na energia mecânica que teria resultado apenas das forças conservadoras, incluindo as potenciais mudanças de energia, e adicionar a ela o trabalho feito, com o sinal adequado, por quaisquer forças não conservadoras envolvidas.
Exemplo 1. Cálculo da distância percorrida: Quão longe um jogador de basebol desliza
Considerar a situação mostrada na Figura 4, onde um jogador de basebol desliza para uma paragem em terreno plano. Usando considerações energéticas, calcular a distância a que desliza o jogador de basebol de 65,0 kg, dado que a sua velocidade inicial é de 6,00 m/s e a força de fricção contra ele é uma constante 450 N.

Figure 4. O jogador de basebol desliza para uma paragem numa distância d. No processo, o atrito remove a energia cinética do jogador, fazendo um trabalho igual à energia cinética inicial.
Estratégia
Fricção pára o jogador convertendo a sua energia cinética em outras formas, incluindo a energia térmica. Em termos do teorema trabalho-energia, o trabalho feito por fricção, que é negativo, é adicionado à energia cinética inicial para reduzi-la a zero. O trabalho feito por fricção é negativo, porque f está na direcção oposta à do movimento (ou seja, θ = 180º, e assim porque θ = -1). Assim Wnc = -fd. A equação simplifica a
\frac{1}{2}{mv_{\text{i}}^2-fd=0\\\\
ou
fd=frac{1}{2}{mv_{\text{i}}^2}{mv_{\text{i}}.
Esta equação pode agora ser resolvida para a distância d.
Solução
Solucionando a equação anterior para d e substituindo os rendimentos conhecidos
\begin{array}{lll}d&&\frac{mv_{\text{i}}^2}{2f}\\\text{ }&&\frac{(65.0text{ kg})(6.00}(6.00}text{ m/s})^2}{(2)(450)text{ N}}}text{ { }&&=2.60text{ m}{m}{array}
Discussão
O ponto mais importante deste exemplo é que a quantidade de trabalho não-conservador é igual à alteração da energia mecânica. Por exemplo, é preciso trabalhar mais para parar um camião, com a sua grande energia mecânica, do que para parar um mosquito.
Exemplo 2. Cálculo da distância percorrida: Deslizando por uma Inclinação
P>Ponhamos que o jogador do Exemplo 1 está a subir uma colina com uma inclinação de 5,00º com uma superfície semelhante à do estádio de basebol. O jogador desliza com a mesma velocidade inicial. Determinar até onde desliza.

Figure 5. O mesmo jogador de basebol desliza para uma paragem numa inclinação de 5,00º.
Estratégia
Neste caso, o trabalho feito pela força de atrito não conservadora no jogador reduz a energia mecânica que ele tem desde a sua energia cinética à altura zero, até à energia mecânica final que ele tem ao mover-se através da distância d para atingir a altura h ao longo da colina, com h = d pecado 5,00º. Isto é expresso pela equação KE + PEi + Wnc = KE f + PEf.
Solução
O trabalho feito por fricção é novamente Wnc = -fd; inicialmente a energia potencial é PEi = mg – 0 = 0 e a energia cinética é \text{KE}_{\i}==frac{1}{2}mv_{\i}^2}; as contribuições energéticas finais são KEf = 0 para a energia cinética e PEf = mgh = mgd sin θ para a energia potencial.
Substituindo estes valores dá
\frac{1}{2}{mv_{\text{i}}^2+0+esquerda(-fd\right)=0+mgd\sin{\i}theta
p>Solver isto para d para obter
\begin{array}{lll}d&&\frac{\left(\frac{1}{2}\right)mv_{\text{i}}^2}{f+mg\sin\theta}\\&&\frac{(0.5)(65.0\texto{ kg})(6.00\texto{ m/s})^2}{450\texto{ N}+(65.0\texto{ kg}){esquerda(9.80\texto{ m/s}^2\direita)^sin(5.00^{\circ})^&
=&&2.31text{ m}{m}{end{array}}
Discussão
Como seria de esperar, o jogador desliza uma distância mais curta ao deslizar para cima. Note-se que o problema também poderia ter sido resolvido em termos das forças directamente e do teorema da energia de trabalho, em vez de se utilizar a energia potencial. Este método teria exigido a combinação da força normal e dos vectores de força de gravidade, que já não se anulam mutuamente porque apontam em direcções diferentes, e o atrito, para encontrar a força da rede. Poder-se-ia então utilizar a força da rede e o trabalho da rede para encontrar a distância d que reduz a energia cinética a zero. Aplicando a conservação de energia e utilizando a energia potencial em vez disso, basta considerar o potencial gravitacional de energia mgh, sem combinar e resolver os vectores de força. Isto simplifica consideravelmente a solução.
Fazer ligações: Levar a Investigação-Casa – Determinar o Atrito a partir da Distância de Paragem
Esta experiência envolve a conversão da energia potencial gravítica em energia térmica. Utilizar a régua, livro, e mármore da secção “Making Connections” da Gravitational Potential Energy. Além disso, será necessário um copo de espuma com um pequeno orifício no lado, como mostra a Figura 6. A partir da posição de 10 cm na régua, deixe o mármore rolar para o copo posicionado no fundo da régua. Meça a distância d a taça move-se antes de parar. Que forças o fizeram parar? O que aconteceu à energia cinética do mármore no fundo da régua? Em seguida, colocar o mármore nas posições de 20 cm e 30 cm e medir novamente a distância que a taça se move depois de o mármore entrar nele. Traçar a distância entre o movimento da taça e a posição inicial do mármore na régua. Esta relação é linear?
Com algumas suposições simples, pode utilizar estes dados para encontrar o coeficiente de atrito cinético μk da taça na mesa. A força de fricção f na taça é μkN, onde a força normal N é apenas o peso da taça mais o mármore. A força normal e a força de gravidade não funcionam porque são perpendiculares ao deslocamento da chávena, que se move horizontalmente. O trabalho feito por fricção é fd. Também será necessária a massa do mármore para calcular a sua energia cinética inicial.
É interessante fazer a experiência acima também com um mármore de aço (ou rolamento de esferas). Soltando-o das mesmas posições na régua que fez com o mármore de vidro, a velocidade deste mármore de aço é a mesma que a velocidade do mármore no fundo da régua? É a distância que o copo se move proporcional à massa dos mármores de aço e vidro?

Figure 6. Rolagem de um mármore por uma régua para dentro de um copo de espuma.
PhET Explorations: A Rampa
Explorar forças, energia e trabalho ao empurrar objectos domésticos para cima e para baixo de uma rampa. Baixar e subir a rampa para ver como o ângulo de inclinação afecta as forças paralelas que actuam no armário de arquivo. Os gráficos mostram forças, energia e trabalho.
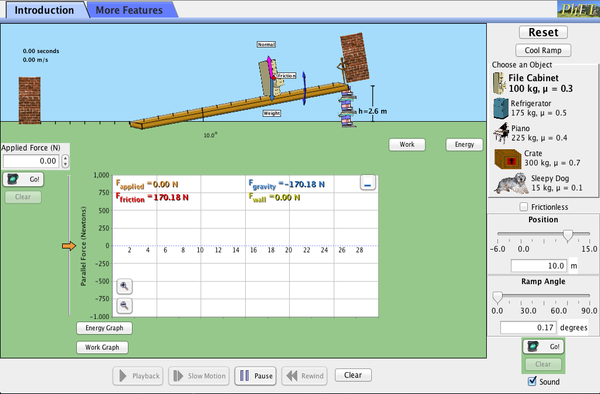
Click para descarregar. Executar utilizando Java.
Secção Resumo
- Uma força não-conservadora é aquela para a qual o trabalho depende do caminho.
- Fricção é um exemplo de uma força não-conservadora que altera a energia mecânica em energia térmica.
- Work Wnc feito por uma força não-conservadora altera a energia mecânica de um sistema. Em forma de equação, Wnc = ΔKE + ΔPE ou, equivalentemente, KEi + PEi + Wnc = KEf + PEf.
- Quando ambas as forças conservadoras e não conservadoras actuam, a conservação de energia pode ser aplicada e utilizada para calcular o movimento em termos das energias potenciais conhecidas das forças conservadoras e do trabalho realizado pelas forças não conservadoras, em vez de encontrar o trabalho da rede a partir da força da rede, ou ter de aplicar directamente as leis de Newton.
Problemas & Exercícios
- A 60,0-kg esquiador com uma velocidade inicial de 12,0 m/s costeia um aumento de 2,50 m de altura, como mostra a Figura 7. Encontre a sua velocidade final no topo, dado que o coeficiente de atrito entre os seus esquis e a neve é de 0,0800. (Dica: Encontrar a distância percorrida para cima da inclinação assumindo um percurso em linha recta, como mostra a figura)

Figure 7. A energia cinética inicial do esquiador é parcialmente utilizada na subida até ao topo de uma subida.
- (a) A que altura pode um carro subir (motor desengatado) se o trabalho feito por fricção for insignificante e a sua velocidade inicial for 110 km/h? (b) Se, na realidade, um carro de 750 kg com uma velocidade inicial de 110 km/h for observado a subir uma colina até uma altura de 22,0 m acima do seu ponto de partida, quanta energia térmica foi gerada por fricção? c) Qual é a força média de atrito se a colina tiver uma inclinação de 2,5º acima da horizontal?
Glossary
força não-conservadora: uma força cujo trabalho depende do caminho seguido entre as configurações inicial e final dadas
fricção: a força entre superfícies que se opõe a uma desliza sobre a outra; o atrito transforma a energia mecânica em energia térmica
Select Solutions to Problems & Exercícios
1. 9,46 m/s