p>Voltar ao Índice de Lições | Fazer as Lições por Ordem | Página de fácil impressãobr>>p> Factorials
Factorials são coisas muito simples. São apenas produtos, indicados por um ponto de exclamação. Por exemplo, “quatro factoriais” é escrito como “4!” e significa 1×2×3×4 = 24. Em geral, n! (“enn factorial”) significa o produto de todos os números inteiros de 1 a n; ou seja, n! = 1×2×3×…×n.
(Por várias razões, 0! é definido como sendo igual a 1, e não 0. Memorize isto agora: 0! = 1.)
- Avalie 6!
1×2×3×4×5×6 = 720
Muitas (a maioria?) calculadoras podem avaliar os factores para si. Por exemplo, o comando factorial está disponível no menu “probabilidade” numa das minhas calculadoras:

Look for a ” ! “, ou consulte o manual do seu proprietário.
- Simplifique 12! Copyright © Elizabeth Stapel 2004-2011 Todos os direitos reservados
12! = 1×2×3×4×… Que se lixe isto! Onde está a minha calculadora…?

12! = 479001600
Advertisement
Quando começar a fazer combinações, permutações, e probabilidades, estará a simplificar expressões que têm factores nos numeradores e nos denominadores. Por exemplo:
- Simplificar o seguinte:
![]()
Posso fazer isto na minha calculadora:
 screen shot: 6!/4! = 30
screen shot: 6!/4! = 30
P>Eu também posso trabalhar a partir da definição de um factorial:
![]()
Em qualquer dos casos, 6! ÷ 4! = 30
Nota como fui capaz de cancelar um monte de números no problema anterior. Isto deve-se à forma como os factores são definidos, e esta propriedade pode simplificar muito o seu trabalho.
- Simplificar o seguinte:
![]()
Dispositivo, posso cancelar os factores 1 a 14 que serão comuns tanto ao 17! como ao 14! Depois posso simplificar o que resta a obter:
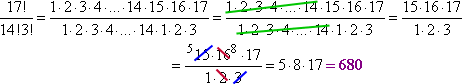
Nota como encurtei o que tinha de escrever deixando uma lacuna (a “elipse”, ou triplo-período) no meio. Esta lacuna – e-cancelamento tornar-se-á útil mais tarde (como no cálculo, onde se utilizará muito esta técnica), especialmente quando se lida com expressões que a calculadora não consegue lidar. Por exemplo:
- Simplificar o seguinte:
![]()
A minha calculadora não pode avaliar isto para mim, uma vez que estou a lidar com variáveis em vez de números. Vou ter de simplificar isto à mão. Para o fazer, vou escrever os factores, usando o suficiente dos factores para ter coisas que podem ser canceladas. Pensando nos problemas de “números” de palavras, números inteiros consecutivos são uma unidade à parte, por isso os factores no produto (n + 2)! são da forma:
- p>1×2×3×4×…×(n – 1)×(n)×(n + 1)×(n + 1)×(n + 2)
Voltando à lista de factores até “n – 1”, criei uma lista de factores que podem cancelar:
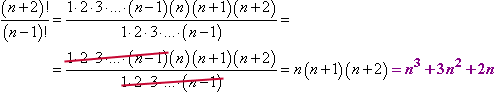
Toma nota da forma como lidei com esse cancelamento. Expandi as expressões factoriais o suficiente para poder ver onde poderia cancelar os factores duplicados. Apesar de não ter ideia do que n poderia ser, ainda assim podia cancelar. Arquive esta técnica no seu cérebro, porque mesmo que não precise dela agora, quase de certeza que vai precisar dela mais tarde.
Para informações sobre como encontrar o número de zeros no fim de um factorial (como “Quantos zeros estão no fim de 23! depois de o multiplicar?”), olhe para esta nota.
Top | Voltar ao Índice
|
Cite este artigo como: |
Stapel, Elizabeth. “Factorials”. Purplemath. Disponível de 2016
|