Se o número de fendas num obstáculo for grande, a nitidez do padrão é melhorada, os máximos ficam mais estreitos. Os obstáculos com um grande número de fendas (mais de, digamos, 20 ao milímetro) são chamados grelhas de difracção. Estas foram desenvolvidas pela primeira vez por Fraunhofer no final do século XVIII e consistiam em fios de prata finos enrolados em dois parafusos paralelos, dando cerca de 30 obstáculos ao milímetro.
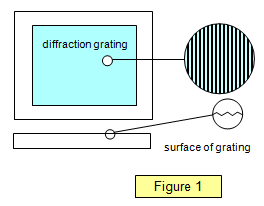
Desde então muitas melhorias foram feitas, em 1882 Rowland utilizou um diamante para governar linhas finas no vidro, as cristas actuando como as fendas e as réguas como os obstáculos (Ver Figura 1). Usando este método é possível obter grades de difracção com até 3000 linhas por milímetro, embora grades ‘grosseiras’ com cerca de 500 linhas por milímetro sejam melhores para uso geral.
Em muitas escolas dois tipos são de uso comum, um com 300 linhas por mm e o outro com 80 linhas por mm.
Redes de reflexão são também utilizadas, onde a imagem difracta é vista após reflexão a partir de uma superfície regida. Um exemplo muito bom de uma grelha de difracção de reflexão é um CD. Um DVD com regras mais finas dá um padrão de difracção muito mais amplo.
A teoria das ondas e a grelha de difracção
>br>
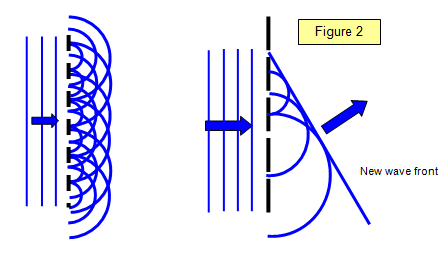
p>Figure 2 mostra a construção Huygens para uma grelha. Pode-se ver como as ondas circulares difratadas de cada fenda se juntam em certas direcções para dar uma onda difratada que tem uma frente de onda plana tal como as ondas que batem na grelha a partir da esquerda. Esta onda plana é formada pelo desenho da linha que encontra todas as pequenas ondas circulares e é chamada um envelope de todas estas pequenas ondas secundárias.br>
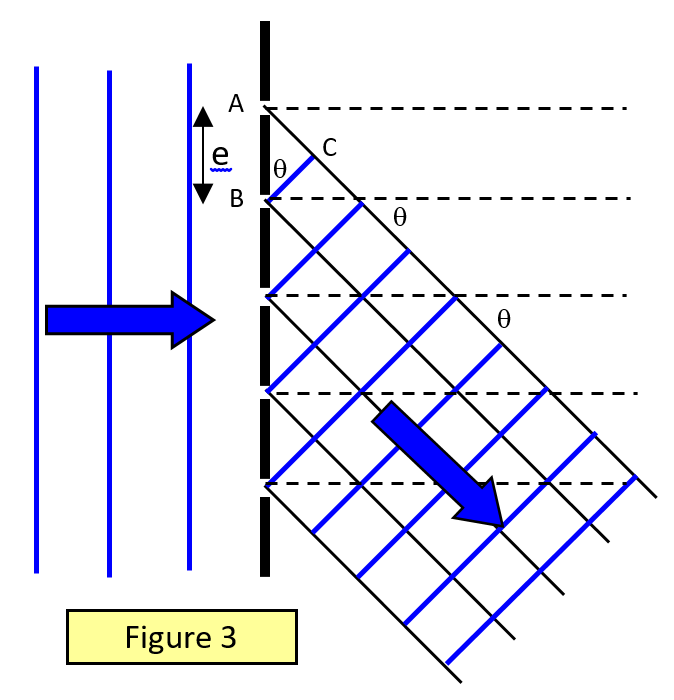
A fórmula da grelha difractiva
Considerar um feixe paralelo de luz incidente normalmente numa grelha difractiva com um espaçamento e (o espaçamento da grelha é o inverso do número de linhas por unidade de comprimento). Considerar a luz que é difraída num ângulo q em relação ao normal e proveniente de pontos correspondentes nas fendas adjacentes (Figura 3).
Para um máximo a diferença de percurso = AC = mλ
But AC = e sinθ. Portanto, para um máximo:
br>
mλ = e sinθ
where m = 0, 1, 2,3…
p> O número m é conhecido como a ordem do espectro, ou seja, forma-se um espectro de primeira ordem para m = 1, e assim por diante.
Se for utilizada luz de um único comprimento de onda, como a de um laser, então ocorre uma série de linhas afiadas, uma linha para cada ordem do espectro. Com uma fonte de luz branca, forma-se uma série de espectros com a luz do comprimento de onda mais curto com o menor ângulo de difracção.
Ao derivarmos a fórmula acima, assumimos que o feixe incidente está em ângulo recto com a face da grelha. Se não for este o caso, deve ser dada uma margem. A forma mais simples é medir a posição do primeiro espectro de ordem em cada lado do centro, registar o ângulo entre estas posições e depois reduzi-lo para metade, como mostrado na Figura 4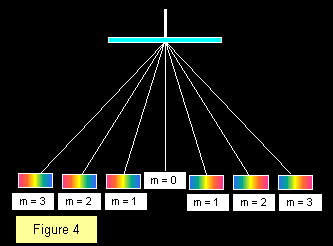.>br>
br>
O número de ordens de espectros visíveis com uma determinada grade depende do espaçamento da grade, sendo mais espectros visíveis com grades mais grosseiras. A face governada da grelha deve sempre apontar para longe da luz incidente para evitar erros devidos a mudanças de direcção por causa da refracção no vidro. O diagrama mostra uma franja branca central com três espectros de cada lado dando um total de sete imagens.
(Ver problema de exemplo )
1. Calcular o comprimento de onda da luz monocromática onde a imagem de segunda ordem é difratada através de um ângulo de 25o usando uma grelha de difracção com 300 linhas por milímetro.
Espaçamento da grelha (e) = 10-3/300 m = 3.3×10-6 m
Comprimento de onda (l) = esin25/2 = /2 = 6,97×10-7 m = 697 nm
2. Calcular o número máximo de ordens visíveis com uma grelha de difracção de 500 linhas por milímetro, usando uma luz de comprimento de onda de 600 nm.
Ângulo máximo de difracção = 90o e = 10-3/500 = 2×10-6 m
aqui m = esinq/l = 2×10-6/600×10-9 = 3,33
aqui o número máximo de ordens = 3, e um total de sete imagens da fonte podem ser vistas (três de cada lado de uma imagem central).
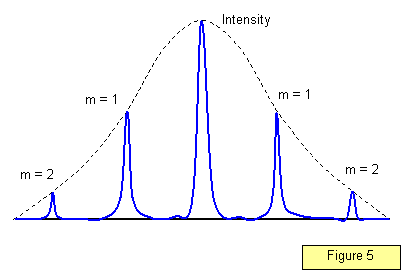br>>p> A distribuição da intensidade no padrão de difracção para um grande número de fendas é mostrada na Figura 5. Note-se que os máximos se tornam muito mais nítidos; quanto maior o número de fendas por metro, mais bem definidos são os máximos.
A difracção da luz de cádmio ou mercúrio é utilizada para determinar a separação de duas linhas num circuito integrado. Foram obtidos os seguintes resultados para as imagens difraccionadas de segunda ordem para diferentes comprimentos de onda. Utilizá-los para traçar um gráfico linear adequado e, a partir daí, determinar o espaçamento médio dos fios no circuito.
| Comprimento de onda/nm | Angulo de difracção (o) |
| 468 | 28.0 |
| 480 | 28.7 |
| 509 | 31.0 |
| 546 | 33.0 |
| 577 | 35.5 |
| 644 | 40.0 |