⇐ Tópico anterior|Próximo tópico ⇒ Índice
Antes de fazer uma experiência, deve realizar uma análise de poder para estimar o número de observações necessárias para ter uma boa probabilidade de detectar o efeito que procura.
Introdução
Quando se está a conceber uma experiência, é uma boa ideia estimar o tamanho da amostra de que necessitará. Isto é especialmente verdade se estiver a propor fazer algo doloroso para os humanos ou outros vertebrados, onde é particularmente importante minimizar o número de indivíduos (sem tornar o tamanho da amostra tão pequeno que toda a experiência seja uma perda de tempo e sofrimento), ou se estiver a planear uma experiência muito demorada ou cara. Foram desenvolvidos métodos para muitos testes estatísticos para estimar o tamanho da amostra necessária para detectar um determinado efeito, ou para estimar o tamanho do efeito que pode ser detectado com um determinado tamanho de amostra.
A fim de fazer uma análise de poder, é necessário especificar um tamanho de efeito. Esta é a dimensão da diferença entre a sua hipótese nula e a hipótese alternativa que espera detectar. Para a investigação biológica aplicada e clínica, pode haver um tamanho de efeito muito definido que deseje detectar. Por exemplo, se estiver a testar um novo champô para cães, o departamento de marketing da sua empresa poderá dizer-lhe que a produção do novo champô só valeria a pena se fizesse um pêlo de cão pelo menos 25% mais brilhante, em média. Esse seria o seu tamanho de efeito, e utilizá-lo-ia ao decidir quantos cães precisaria de passar pelo reflectómetro canino.
Ao fazer investigação biológica básica, muitas vezes não sabe a diferença que procura, e a tentação pode ser apenas utilizar o maior tamanho de amostra que pode pagar, ou utilizar um tamanho de amostra semelhante a outras investigações no seu campo. Deve ainda fazer uma análise de poder antes de fazer a experiência, apenas para ter uma ideia do tipo de efeitos que pode detectar. Por exemplo, alguns malucos anti-vacinação propuseram que o governo dos EUA realizasse um grande estudo de crianças não vacinadas e vacinadas para ver se as vacinas causam autismo. Não é claro qual seria o tamanho do efeito interessante: 10% mais autismo num só grupo? 50% mais? duas vezes mais? Contudo, fazer uma análise de poder mostra que mesmo que o estudo incluísse todas as crianças não vacinadas nos Estados Unidos com idades compreendidas entre 3 e 6 anos, e um número igual de crianças vacinadas, teria de haver mais 25% de autismo num grupo para que houvesse uma grande probabilidade de ver uma diferença significativa. Um estudo mais plausível, de 5.000 crianças não vacinadas e 5.000 vacinadas, detectaria uma diferença significativa com elevada potência apenas se houvesse três vezes mais autismo num grupo do que no outro. Porque é improvável que haja uma diferença tão grande no autismo entre crianças vacinadas e não vacinadas, e porque não encontrar uma relação com um estudo deste tipo não convenceria os antivirais de que não havia relação (nada os convenceria de que não há relação – é isso que os torna anormais), a análise de poder diz-lhe que um estudo tão grande e caro não valeria a pena.
Parâmetros
Há quatro ou cinco números envolvidos numa análise de poder. É necessário escolher os valores para cada um antes de fazer a análise. Se não tiver uma boa razão para utilizar um determinado valor, pode tentar valores diferentes e observar o efeito no tamanho da amostra.
Tamanho do efeito
O tamanho do efeito é o desvio mínimo da hipótese nula que se espera detectar. Por exemplo, se estiver a tratar galinhas com algo que espera alterar a proporção de sexo dos seus pintos, poderá decidir que a alteração mínima na proporção de sexos que procura é de 10%. Dir-se-ia então que o tamanho do seu efeito é 10%. Se estiver a testar algo para que as galinhas ponham mais ovos, o tamanho do efeito poderá ser de 2 ovos por mês.
Ocasionalmente, terá uma boa razão económica ou clínica para escolher um determinado tamanho de efeito. Se estiver a testar um suplemento alimentar para galinhas que custa $1,50 por mês, só está interessado em saber se este produzirá mais de $1,50 de ovos extra por mês; saber que um suplemento produz um ovo extra de 0,1 por mês não é informação útil para si, e não precisa de conceber a sua experiência para descobrir isso. Mas para a maioria da investigação biológica básica, o tamanho do efeito é apenas um número redondo agradável que retirou do seu rabo. Digamos que está a fazer uma análise de poder para um estudo de uma mutação numa região promotora, para ver se ela afecta a expressão genética. Quão grande é a mudança na expressão génica que procura: 10%? 20%? 50%? É um número bastante arbitrário, mas terá um efeito enorme no número de ratos transgénicos que darão as suas pequenas e caras vidas pela sua ciência. Se não tiver uma boa razão para procurar um determinado tamanho de efeito, mais vale admitir isso e desenhar um gráfico com tamanho de amostra no eixo X e tamanho de efeito no eixo Y. G*Power fará isto por si.
Alpha
Alpha é o nível de significância do teste (o valor P), a probabilidade de rejeitar a hipótese nula mesmo que seja verdadeira (um falso positivo). O valor habitual é alfa=0,05. Algumas calculadoras de potência utilizam o alfa de uma cauda, o que é confuso, visto que o alfa de duas caudas é muito mais comum. Certifique-se de que sabe qual está a usar.
Beta ou potência
Beta, numa análise de potência, é a probabilidade de aceitar a hipótese nula, mesmo que seja falsa (um falso negativo), quando a diferença real é igual ao tamanho do efeito mínimo. O poder de um teste é a probabilidade de rejeitar a hipótese nula (obtendo um resultado significativo), quando a diferença real é igual ao tamanho mínimo do efeito. O poder é de 1-beta. Não há um consenso claro sobre o valor a usar, por isso este é outro número que se tira do rabo; um poder de 80% (equivalente a um beta de 20%) é provavelmente o mais comum, enquanto algumas pessoas usam 50% ou 90%. O custo para si de um falso negativo deve influenciar a sua escolha do poder; se realmente, realmente, quiser ter a certeza de que detecta o tamanho do seu efeito, vai querer usar um valor mais alto para o poder (beta mais baixo), o que resultará num tamanho de amostra maior. Algumas calculadoras de potência pedem-lhe que introduza o beta, enquanto outras pedem potência (1-beta); tenha muito a certeza de que compreende o que precisa de usar.
Desvio padrão
Para variáveis de medição, também é necessária uma estimativa do desvio padrão. À medida que o desvio padrão se torna maior, torna-se mais difícil detectar uma diferença significativa, pelo que será necessário um tamanho de amostra maior. A sua estimativa do desvio padrão pode provir de experiências-piloto ou de experiências semelhantes na literatura publicada. O seu desvio padrão depois de fazer a experiência é improvável que seja exactamente o mesmo, pelo que a sua experiência será de facto um pouco mais ou menos potente do que tinha previsto.
Para variáveis nominais, o desvio padrão é uma função simples do tamanho da amostra, pelo que não precisa de o estimar separadamente.
Como funciona
Os detalhes de uma análise de potência são diferentes para testes estatísticos diferentes, mas os conceitos básicos são semelhantes; aqui vou usar o teste binomial exacto como exemplo. Imagine que está a estudar as fracturas do pulso, e a sua hipótese nula é que metade das pessoas que partem um pulso parte o pulso direito, e metade parte o esquerdo. Decide que o tamanho mínimo do efeito é 10%; se a percentagem de pessoas que partem o pulso direito for 60% ou mais, ou 40% ou menos, quer ter um resultado significativo do teste binomial exacto. Não faço ideia porque escolheu 10%, mas é isso que vai utilizar. Alfa é 5%, como de costume. Quer que a potência seja 90%, o que significa que se a percentagem de pulsos direitos partidos for realmente 40% ou 60%, quer um tamanho de amostra que produza um resultado significativo (P<0.05) 90% do tempo, e um resultado não significativo (que seria um falso negativo neste caso) apenas 10% do tempo.
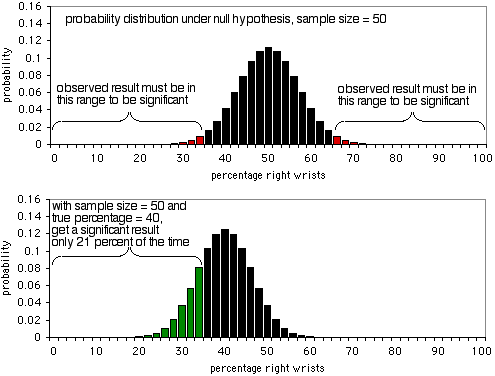

O primeiro gráfico mostra a distribuição de probabilidade sob a hipótese nula, com um tamanho de amostra de 50 indivíduos. Se a hipótese nula for verdadeira, verá menos de 36% ou mais de 64% das pessoas a partirem os pulsos direitos (um falso positivo) cerca de 5% do tempo. Como mostra o segundo gráfico, se a percentagem verdadeira for 40%, os dados da amostra serão menos de 36 ou mais de 64% apenas 21% do tempo; obterá um verdadeiro positivo apenas 21% do tempo, e um falso negativo 79% do tempo. Obviamente, um tamanho de amostra de 50 é demasiado pequeno para esta experiência; apenas produziria um resultado significativo 21% do tempo, mesmo que houvesse uma proporção de 40:60 de pulsos direitos partidos para pulsos esquerdos.
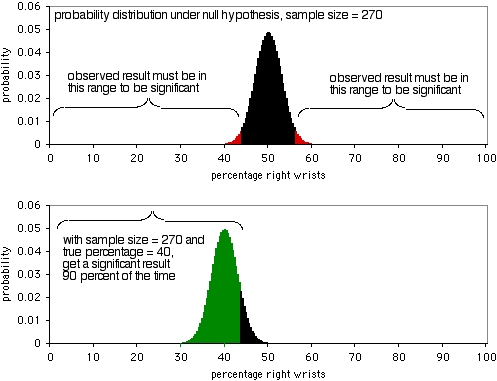

O gráfico seguinte mostra a distribuição de probabilidade sob a hipótese nula, com um tamanho de amostra de 270 indivíduos. Para ser significativo ao nível P<0,05, o resultado observado teria de ser menos de 43,7% ou mais de 56,3% de pessoas a partirem os pulsos direitos. Como mostra o segundo gráfico, se a percentagem verdadeira for de 40%, os dados da amostra serão estes extremos 90% do tempo. Um tamanho de amostra de 270 é bastante bom para esta experiência; produziria um resultado significativo 90% do tempo se houvesse uma proporção de 40:60 de pulsos partidos do lado direito para o esquerdo. Se a proporção de pulsos partidos da direita para a esquerda estiver mais longe de 50:50, terá uma probabilidade ainda maior de obter um resultado significativo.
Exemplos
Planeia-se cruzar ervilhas que são heterozigotas para a cor de ervilha amarela/verde, onde o amarelo é dominante. A proporção esperada na descendência é de 3 Amarelos: 1 verde. Pretende-se saber se as ervilhas amarelas estão realmente mais ou menos em forma, o que pode aparecer como uma proporção diferente de ervilhas amarelas do que o esperado. Decide arbitrariamente que quer um tamanho de amostra que detecte uma diferença significativa (P<0,05) se houver mais ou menos 3% de ervilhas amarelas do que o esperado, com uma potência de 90%. Os dados serão testados utilizando o teste binomial exacto de goodness-of-fit se o tamanho da amostra for suficientemente pequeno, ou um teste G de goodness-of-fit se o tamanho da amostra for maior. A potência de análise é a mesma para ambos os testes.
Using G*Power como descrito para o teste exacto de goodness-of-fit, o resultado é que seriam necessárias 2109 ervilhas se se quiser obter um resultado significativo (P<0,05) 90% do tempo, se a verdadeira proporção de ervilhas amarelas for 78%, e 2271 ervilhas se a verdadeira proporção for 72% amarela. Uma vez que estaria interessado num desvio em qualquer direcção, usa-se o maior número, 2271. É um monte de ervilhas, mas fica reconfortado por ver que não é um número ridículo. Se quiser detectar uma diferença de 0,1% entre os números esperados e os observados de ervilhas amarelas, pode calcular que vai precisar de 1.970.142 ervilhas; se é isso que precisa de detectar, a análise do tamanho da amostra diz-lhe que vai ter de incluir um robot classificador de ervilhas no seu orçamento.
Os dados de exemplo para o teste t de duas amostras mostram que a altura média na secção das 14 horas da Análise de Dados Biológicos era de 66,6 polegadas e a altura média na secção das 17 horas era de 64,6 polegadas, mas a diferença não é significativa (P=0,207). Pretende-se saber quantos estudantes teriam de amostrar para ter uma probabilidade de 80% de uma diferença tão grande ser significativa. Utilizando G*Power, tal como descrito na página de teste t de duas amostras, introduza 2,0 para a diferença em meios. Utilizando a função STDEV no Excel, calcular o desvio padrão para cada amostra nos dados originais; é 4,8 para a amostra 1 e 3,6 para a amostra 2. Introduzir 0,05 para alfa e 0,80 para potência. O resultado é 72, o que significa que se os alunos das 17 horas fossem realmente dois centímetros mais curtos que os alunos das 14 horas, seriam necessários 72 alunos em cada turma para detectar uma diferença significativa 80% do tempo, se a verdadeira diferença for realmente de 2,0 centímetros.
Como fazer análises de potência
G*Power
G*Power é um excelente programa gratuito, disponível para Mac e Windows, que fará análises de potência para uma grande variedade de testes. Explicarei como utilizar G*Power para análises de potência para a maioria dos testes deste manual.
R
Salvatore Mangiafico’s R Companion tem programas de amostra R para fazer análises de potência para muitos dos testes deste manual; vá à página para o teste individual e role para o fundo para o programa de análise de potência.
SAS
SAS tem um PROC POWER que pode utilizar para análises de potência. Introduza os parâmetros necessários (que variam consoante o teste) e introduza um período (que simboliza os dados em falta no SAS) para o parâmetro para o qual está a resolver (geralmente ntotal, o tamanho total da amostra, ou npergroup, o número de amostras em cada grupo). Acho que G*Power é mais fácil de usar do que SAS para este fim, por isso não recomendo a utilização de SAS para as suas análises de potência.
⇐ Tópico anterior|Tópico seguinte ⇒ Índice
Esta página foi revista pela última vez a 20 de Julho de 2015. O seu endereço é http://www.biostathandbook.com/power.html. Pode ser citado como:
McDonald, J.H. 2014. Handbook of Biological Statistics (3ª ed.). Sparky House Publishing, Baltimore, Maryland. Esta página web contém o conteúdo das páginas 40-44 na versão impressa.
©2014 por John H. McDonald. Pode provavelmente fazer o que quiser com este conteúdo; consulte a página de permissões para mais detalhes.