Heading

No ano 1072 d.C., Omar Khayyam documentou a duração do ano mais precisa alguma vez calculada – um número ainda suficientemente preciso para a maioria dos fins no mundo moderno. Khayyam foi astrónomo, astrólogo, médico, filósofo e matemático: fez contribuições notáveis em álgebra. A sua poesia é mais conhecida no Ocidente do que qualquer outro poeta não ocidental.

O próprio homem continua a ser algo de enigma. Diferentes biógrafos documentaram-no como um agnóstico divertido e bebedor de vinho; um zoroastriano de armário; um muçulmano sufista; um muçulmano sunita ortodoxo; e um seguidor da filosofia da Grécia Antiga. Todos concordam que ele era um excelente intelectual.

Beginnings

Omar Khayyam nasceu a 18 de Maio de 1048 na grande cidade comercial de Nishapur, no norte da Pérsia. Hoje a cidade encontra-se no Irão. O pai de Omar foi Ebrahim Khayyami, um médico abastado. O nome da mãe de Omar não é conhecido. Alguns autores escreveram que o pai de Omar ganhava a vida a fazer tendas porque Khayyami significa “tent-maker”. No entanto, embora muitos falantes de inglês se chamem Smith, isso não significa que os seus pais tenham passado os dias a martelar metal quente numa bigorna.

A família de Omar era muçulmana. O seu pai parece ter sido relaxado quanto à religião, empregando um matemático chamado Bahmanyar bin Marzban, um devoto da antiga religião persa do zoroastrismo, para ensinar Omar. Bahmanyar tinha sido aluno do grande médico, cientista, e filósofo Avicenna, e deu a Omar uma educação completa em ciência, filosofia e matemática. Khawjah al-Anbari ensinou astronomia a Omar, guiando-o através do Almagest de Ptolomeu.

Na sua adolescência, Omar trabalhou na cirurgia do seu pai aprendendo medicina.

Omar Khayyam celebrou o seu décimo oitavo aniversário em 1066. No mesmo ano, o cometa Halley apareceu nos céus, o Exército Normando de William, o Conquistador, invadiu a Inglaterra, e o pai de Omar, Ebrahim, morreu. Poucos meses após a morte de Ebrahim, o tutor de Omar Bahmanyar também morreu.

Foi o fim de uma era na vida de Omar Khayyam. Era tempo de pôr os assuntos da sua família em ordem e seguir em frente.

Samarkand

Omar Khayyam juntou-se a uma das caravanas regulares fazendo uma viagem de três meses de Nishapur até à grande cidade de Samarkand, que se encontra agora no Uzbequistão. Samarkand era um centro de bolsas de estudo, e Khayyam chegou lá provavelmente em 1068, com 20,

Em Samarkand fez contacto com o velho amigo do seu pai Abu Tahir, que era governador e juiz principal da cidade. Tahir, observando o extraordinário talento de Khayyam com números, deu-lhe um emprego no seu escritório. Logo Khayyam recebeu um emprego na tesouraria do rei.

Enquanto vivia em Samarkand, Khayyam fez um grande avanço em álgebra.

Contribuições de Omar Khayyam para a Ciência

Álgebra

Na escola secundária aprendemos sobre as equações da forma ax2 + bx + c = 0; estas são chamadas equações quadráticas. As equações cúbicas são da forma ax3 + bx2 + cx + d = 0. Naturalmente, as equações cúbicas são mais difíceis de resolver que as quadráticas.

Khayyam conjecturou correctamente que não é possível resolver equações cúbicas utilizando as ferramentas geométricas tradicionais da Grécia Antiga de Straightedge e bússola. Outros métodos são necessários.

Aos 22 anos de idade, em 1070, Khayyam publicou uma das suas maiores obras: Tratado sobre Demonstração de Problemas de Álgebra e Equilíbrio. Nele mostrou que uma equação cúbica pode ter mais do que uma solução. Mostrou também como as intersecções de secções cónicas como parábolas e círculos podem ser utilizadas para produzir soluções geométricas de equações cúbicas. Arquimedes tinha de facto começado a trabalhar neste campo mais de mil anos antes, quando considerou o problema específico de encontrar a proporção do volume de uma parte de uma esfera para outra. Khayyam considerou o problema de uma forma mais geral e metódica.

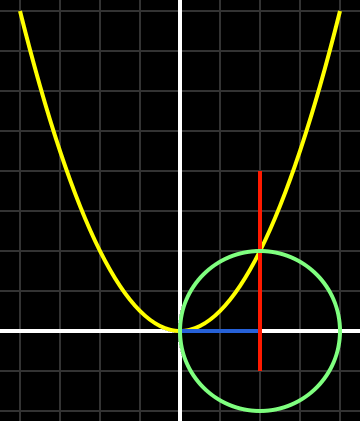
Na linguagem da matemática moderna, a solução de Khayyam para a equação x3 + a2x = b apresenta uma parábola da equação x2 = ay, um círculo com diâmetro b/a2, e uma linha vertical através do ponto de intersecção. A solução é dada pela distância no eixo x entre a origem e a linha vertical (vermelha). Imagem de Pieter Kuiper.

Soluções de Khayyam evitaram coeficientes negativos e raízes negativas porque os números negativos não eram reconhecidos na matemática islâmica. (Algumas culturas, contudo, tinham incorporado números negativos na matemática – por exemplo Brahmagupta tinha introduzido números negativos na matemática indiana 400 anos antes.)

Embora a realização de Khayyam fosse magnífica, ele estava pessoalmente desapontado com a necessidade de utilizar a geometria para resolver equações cúbicas – ele esperava descobrir um algoritmo utilizando apenas álgebra.

Tratado sobre Demonstração de Problemas de Álgebra e Equilíbrio estabeleceu Khayyam como um matemático de primeira linha, e a sua reputação espalhou-se rapidamente por toda a Pérsia.

Segundo a descoberta de Khayyam, houve pouco progresso significativo nas equações cúbicas até 1535, quando Niccolo Tartaglia encontrou soluções gerais para todas as equações cúbicas.

A álgebra de Khayyam não era o sistema de letras e sinais que usamos hoje. A sua álgebra era expressa em palavras. Assim, onde hoje escrevemos:

Solve para x:

x2 + 6 = 5x

Khayyam escreveu: Qual é a quantidade de um quadrado para que quando se lhe adicionam 6 dirhams, ele se torne igual a cinco raízes desse quadrado?

Álgebra de ligação e Geometria

Álgebra e Geometria foram ligadas com sucesso por Pierre de Fermat e René Descartes nos anos 1600, resultando no moderno sistema de coordenadas x-y.

O trabalho de Khayyam com os cúbicos tinha-lhe assegurado que a álgebra e a geometria estavam ligadas, e ele citou os Elementos de Euclides para apoiar a ideia:

Quem pensa que a álgebra é um truque para obter incógnitas pensou-o em vão. Não se deve prestar atenção ao facto de que a álgebra e a geometria são diferentes na aparência. As álgebras são factos geométricos que são provados pelas Propostas 5 e 6 do Livro 2 dos Elementos de Euclides.

Duração do Ano

Em 1073, Khayyam recebeu um convite para a cidade persa de Isfahan, capital do Império Seljuk, para preparar um calendário que funcionasse de forma ordenada e fosse preciso para sempre – esta foi uma era em que a duração dos anos era regularmente alterada.

Khayyam foi convidado pelos dois homens mais poderosos do Império Seljuk, dos quais a Pérsia fazia parte: estes eram Malik Shah, Sultão do império, e Nizam al-Mulk, seu vizir.

Khayyam recrutou outros cientistas talentosos para o acompanharem a Isfahan em 1074. Aí recebeu um salário extraordinariamente elevado e desfrutou de um estilo de vida privilegiado. Malik Shah pagou a Khayyam para fundar um observatório com o objectivo inicial de fazer observações dos céus durante 30 anos, durante os quais Saturno, o planeta mais distante então conhecido, completaria uma órbita.

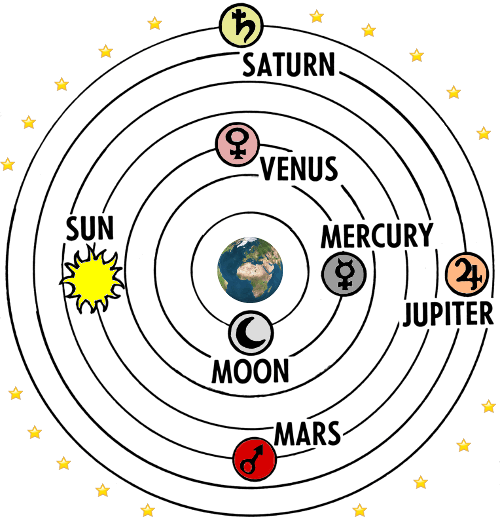p> Universo de Ptolomeu – o modelo aceite por Omar Khayyam.

Durante o seu tempo em Isfahan, Khayyam mediu a duração de um ano – para ser específico a duração do ano tropical – com notável precisão e precisão.

Khayyam descobriu que 1.029.983 dias fizeram 2.820 anos. Isto dá uma duração de um ano tropical de 365.2422 dias a sete números significativos. Embora se tenha tornado moda citar mais casas decimais do que isto, a entrada de Khayyam de 1.029.983 dias contém sete números significativos, por isso não é razoável citar mais do que este número de números significativos na duração do ano calculado.

Hoje sabemos que a duração de um ano tropical na realidade muda em até 30 minutos de ano para ano. A duração média de um ano tropical citada hoje é de 365,242189 dias, que para sete números significativos é de 365,2422 dias – exactamente o número a que Khayyam chegou há quase mil anos. A duração de um ano tropical está também a aumentar muito ligeiramente à medida que o tempo passa, embora não o suficiente entre a era de Khayyam e a nossa para ser perceptível numa escala de sete figuras significativas.

Malik Shah introduziu o novo calendário de Khayyam no Império Seljuk a 15 de Março de 1079. Foi usado até ao século XX.

O Postulado Paralelo

Os 13 livros dos Elementos de Euclides publicados em cerca de 300 AC foram provavelmente os livros mais influentes de toda a história da matemática. Os Elementos tinham sido construídos sobre cinco postulados geométricos – por outras palavras, cinco coisas que foram assumidas como verdadeiras sobre geometria: por exemplo, todos os ângulos rectos são iguais uns aos outros.

O quinto dos cinco postulados de Euclides era o postulado paralelo. O postulado paralelo provou ser uma fonte de enigmas, irritação e alegria para os matemáticos durante milénios. A alegria era geralmente de curta duração, pertencente aos matemáticos que pensavam ter provado que o postulado só se desiludia quando um erro era identificado na sua “prova”.

Euclid tinha considerado uma linha recta que atravessava duas outras linhas rectas. Ele observou a situação quando os ângulos interiores (mostrados na imagem abaixo) aumentam para menos de 180 graus. Nestas circunstâncias, ele disse que as duas linhas rectas acabarão por se encontrar do lado dos dois ângulos que aumentam para menos de 180 graus.

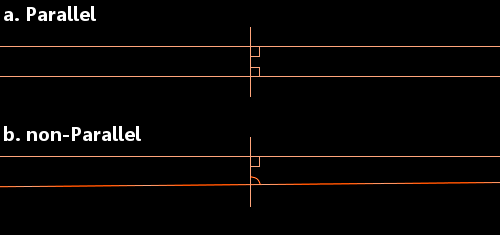
a. Quando cada ângulo é de 90 graus, as linhas são paralelas.
b. Se um ou ambos os ângulos forem inferiores a 90 graus, as linhas encontrar-se-ão.

p>Desde a primeira vez que os Elementos foram publicados, os matemáticos tinham tentado utilizar os primeiros quatro postulados de Euclides para provar o postulado paralelo. Estavam condenados ao fracasso. Sabemos agora que é impossível provar o postulado paralelo usando os outros postulados de Euclid.

p>A tentativa de Omar Khayyam foi interessante. Nas suas Explicações das Dificuldades dos Postulados nos Elementos de Euclides, pede aos seus leitores que considerem uma linha recta AB:

P> Pede aos seus leitores que considerem duas linhas iguais que são perpendiculares ao AB e vê três arranjos possíveis, que podem produzir figuras de quatro lados:

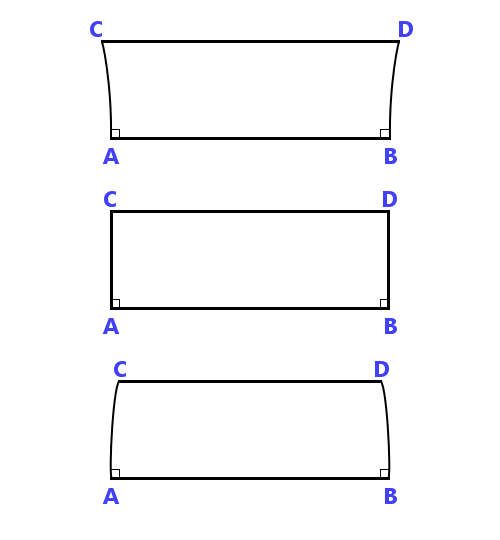
Ele refuta então a possibilidade de que os ângulos C e/ou D possam ser qualquer outra coisa que não os ângulos rectos e na imagem acima apenas a opção central é possível. Assim, ele acredita ter provado o postulado paralelo. De facto, ele não o fez, tudo o que fez foi declará-lo de uma forma diferente.

O que é interessante para os historiadores da matemática é que nas ideias de Khayyam – mostradas aproximadamente nas imagens acima – eles podem ver os primeiros vislumbres da geometria não-euclidiana.

alguns detalhes pessoais e o fim

Detalhes completos da vida pessoal de Khayyam não são conhecidos. Acredita-se que ele tenha casado e tido pelo menos um filho e uma filha.

Em 1092, Malik Shah e o seu vizir morreram ambos – o primeiro provavelmente por envenenamento, o segundo por assassinato. Khayyam escondeu-se durante a resultante luta pelo poder. A sua sobrevivência dependia de se deitar baixo. Ele tinha sido o médico pessoal de Malik Shah e tornou-se seu amigo pessoal próximo – o que o tinha tornado inimigo – e a poesia de Khayyam sugere que o seu comportamento pode não ter sido devotamente religioso – e isto também o tinha tornado inimigo. Khayyam na realidade não publicou nenhuma poesia durante a sua vida. Algumas das suas reflexões teriam potencialmente colocado a sua vida em perigo.

Após a luta pelo poder, Khayyam levou cerca de 20 anos para se reabilitar completamente e para ele emergir novamente, aos 64 anos de idade, na companhia de pessoas poderosas. Contudo, ele recusou-se a ensinar. Um dos seus poemas sugere porque é que isto poderia ser:

Os segredos que o meu livro de amor criou,
Não se pode contar por medo de perder a cabeça;
Posto que ninguém está apto a aprender, ou se preocupa em saber,
É melhor que todos os meus pensamentos permaneçam por dizer.

Omar Khayyam morreu aos 83 anos de idade na sua cidade natal, Nishapur, a 4 de Dezembro de 1131. Foi enterrado num túmulo cuja localização tinha escolhido, num pomar onde a flor cairia duas vezes por ano.

A poesia de Khayyam foi popularizada nos anos 1800 pelas traduções de Edward FitzGerald no Rubaiyat de Omar Khayyam. Khayyam tornou-se tão admirado no Ocidente que em 1963 o Xá do Irão teve o seu túmulo exumado e os restos mortais de Khayyam mudados para um enorme mausoléu construído propositadamente em Nishapur, onde os turistas podiam prestar homenagem ao grande poeta.

Terminaremos com uma das mais famosas e evocativas quatraínas de Khayyam:

"Omar Khayyam." Famous Scientists. famousscientists.org. 5 Nov. 2016. Web. <www.famousscientists.org/omar-khayyam/>.