O método dos multiplicadores de Lagrange é o cavalo de batalha do economista para a resolução de problemas de optimização. A técnica é uma peça central da teoria económica, mas infelizmente é geralmente mal ensinada.
A maior parte dos livros didácticos concentra-se em fórmulas mecânicas, deixando os estudantes perplexos sobre o porquê de funcionar de facto para começar. Neste post, vou explicar uma forma simples de ver porque é que os multiplicadores Lagrange fazem realmente o que fazem – ou seja, resolvem problemas de optimização constrangidos através do uso de uma função Lagrangiana semi-misteriosa.
alguns antecedentes
Antes de poder ver porque é que o método funciona, é preciso saber algo sobre os gradientes. Para funções de uma variável existe – normalmente – uma primeira derivada. Para as funções de n variáveis, existem n primeiras derivadas. Um gradiente é apenas um vector que recolhe todas as primeiras derivadas parciais da função num só local.
p>Cada elemento no gradiente é uma das primeiras derivadas parciais da função. Uma maneira fácil de pensar num gradiente é que se escolhermos um ponto em alguma função, isso dá-nos a “direcção” que a função está a seguir. Se a nossa função for rotulada
a notação para o gradiente de f é
O mais importante a saber sobre inclinações é que apontam sempre na direcção da inclinação mais acentuada de uma função num determinado ponto. Para ajudar a ilustrar isto, dê uma vista de olhos ao desenho abaixo. Ilustra como os gradientes funcionam para uma função de duas variáveis de x1 e x2,
A função f no desenho forma uma colina. Em direcção ao pico desenhei duas regiões onde mantemos a altura de f constante em algum nível a. Estas são chamadas curvas de nível de f, e são marcadas f = a1, e f = a2.
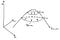
Imagine-se em pé numa dessas curvas de nível. Pense num trilho para caminhadas na encosta de uma montanha. De pé no trilho, em que direcção é a mais íngreme da montanha? É evidente que a direcção mais íngreme é em linha recta, perpendicular ao trilho. No desenho, estes caminhos de subida mais íngremes são marcados com setas. Estes são os desníveis
em vários pontos ao longo das curvas de nível. Tal como a caminhada mais íngreme é sempre perpendicular à nossa trilha, os gradientes de f são sempre perpendiculares às suas curvas de nível.
Esta é a ideia chave aqui: as curvas de nível são onde
e
Como funciona o Método
Para ver como funcionam os multiplicadores de Lagrange, ver o desenho abaixo. Redefini a função f de cima, juntamente com uma restrição g = c. No desenho, a restrição é um plano que atravessa a nossa encosta. Também desenhei algumas curvas de nível de f.

O nosso objectivo aqui é subir o mais alto da colina que pudermos, dado que não nos podemos mover mais alto do que onde a restrição g = c corta a colina.
No desenho, o limite onde a restrição corta a função é marcado com uma linha pesada. Ao longo dessa linha são os pontos mais altos que podemos alcançar sem pisar o nosso constrangimento. É um lugar óbvio para começar a procurar um máximo constrangido.
Imagine caminhadas da esquerda para a direita na linha de constrangimento. À medida que ganhamos elevação, caminhamos através de várias curvas de nível de f. Marquei duas na imagem. Em cada curva de nível, imagine verificar a sua inclinação – ou seja, a inclinação de uma linha tangente a ela – e comparar isso com a inclinação da restrição em que estamos.
Se a nossa inclinação for maior do que a curva de nível, podemos atingir um ponto mais alto na colina se continuarmos a andar para a direita. Se a nossa inclinação for menor que a curva de nível – digamos, para a direita onde a nossa linha de restrição está em declínio – precisamos de recuar para a esquerda para atingir um ponto mais alto.
Quando atingimos um ponto onde a inclinação da linha de restrição é igual à inclinação da curva de nível, já nos movemos o mais alto que podemos. Ou seja, atingimos o nosso máximo constrangido. Qualquer movimento a partir desse ponto irá levar-nos a descer. Na figura, este ponto é marcado com uma grande seta apontando para o pico.
Nesse ponto, a curva de nível f = a2 e a restrição têm a mesma inclinação. Isso significa que são paralelas e apontam na mesma direcção. Mas como vimos acima, as inclinações são sempre perpendiculares às curvas de nível. Assim, se estas duas curvas forem paralelas, os seus gradientes devem também ser paralelos.
Isso significa que os gradientes de f e g apontam ambos na mesma direcção, e diferem no máximo por um escalar. Chamemos a essa escalar “lambda”. Então temos,
Solving for zero, obtemos
Esta é a condição que deve ser mantida quando se atinge o máximo de f sujeito à restrição g = c. Agora, se formos espertos, podemos escrever uma única equação que capte esta ideia. É aqui que entra a familiar equação Lagrangiana:
ou mais explicitamente,
p>Para ver como funciona esta equação, observar o que acontece quando seguimos o procedimento Lagrangiano habitual. Em primeiro lugar, encontramos as três primeiras derivadas parciais de L,
e fixá-los a zero. Ou seja, precisamos de definir o gradiente de L igual a zero. Para encontrar o gradiente de L, tomamos as três derivadas parciais de L em relação a x1, x2 e lambda. Depois colocamos cada uma delas como um elemento num vector 3 x 1. Isso dá-nos o seguinte:
Recordar que temos duas “regras” a seguir aqui. Primeiro, as inclinações de f e g devem apontar na mesma direcção, or
e segundo, temos de satisfazer o nosso constrangimento, ou
O primeiro e segundo elementos do gradiente de L certificam-se de que a primeira regra é seguida. Ou seja, eles forçam
assegurando que os gradientes de f e g apontam ambos na mesma direcção. O terceiro elemento do gradiente de L é simplesmente um truque para garantir que g = c, que é o nosso constrangimento. Na função Lagrangiana, quando tomamos a derivada parcial em relação à lambda, ela simplesmente devolve-nos a nossa equação de restrição original.
Neste ponto, temos três equações em três incógnitas. Assim, podemos resolver isto para os valores óptimos de x1 e x2 que maximizam f sujeitos à nossa restrição. E estamos feitos.
Por isso, o resultado final é que os multiplicadores de Lagrange são realmente apenas um algoritmo que encontra onde o gradiente de uma função aponta na mesma direcção que os gradientes das suas restrições, ao mesmo tempo que satisfaz essas restrições.
Como acontece com a maioria das áreas da matemática, uma vez que se vê até ao fundo das coisas – neste caso, que a optimização é realmente apenas uma escalada, o que todos entendem – as coisas são muito mais simples do que a maioria dos economistas as fazem ser.