A vida útil global de uma estrela é determinada pela sua massa. Uma vez que as estrelas passam cerca de 90% da sua vida a queimar hidrogénio em hélio na sequência principal (EM), a sua “vida útil da sequência principal” é também determinada pela sua massa.
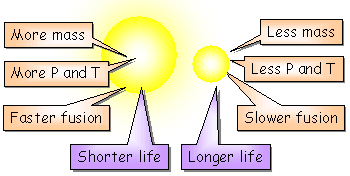
As estrelas maciças precisam de temperaturas e pressões centrais mais elevadas para se suportarem contra o colapso gravitacional, e por esta razão, as reacções de fusão nestas estrelas prosseguem a um ritmo mais rápido do que nas estrelas de massa inferior. O resultado é que as estrelas maciças consomem rapidamente o seu núcleo de hidrogénio e passam menos tempo na sequência principal antes de evoluir para uma estrela gigante vermelha.
Uma expressão para a duração da sequência principal pode ser obtida em função da massa estelar e é geralmente escrita em relação a unidades solares (para uma derivação desta expressão, ver abaixo):
![]()
| onde | t⊙ | >>>>>>>Sol MS Life = 1010 | |
| M⊙ | = | massa solar |
Os tempos de vida das estrelas da sequência principal variam, portanto, entre um milhão de anos para uma massa solar de 40 O-tipo estrela, a 560 mil milhões de anos por um 0.2 estrelas tipo M de massa solar. Dado que o Universo tem apenas 13,7 mil milhões de anos, estes longos períodos de vida da sequência principal para estrelas do tipo M significam que cada estrela M que foi criada ainda está na sequência principal! O Sol, uma estrela do tipo G com uma vida útil da sequência principal de ~ 10 mil milhões de anos, tem actualmente 5 mil milhões de anos – cerca de metade da sua vida útil da sequência principal.
Derivação
A luminosidade da estrela é a energia libertada por unidade de tempo. Para as estrelas da sequência principal, a energia provém da fusão de hidrogénio e nós temos:
L = E/t
| onde | L | = | a luminosidade da estrela |
| E | = | energia produzida por H burning | |
| == | tempo |
Podemos usar a energia de Einstein-equação de massa para calcular a energia produzida pela queima de hidrogénio. A massa convertida em energia através da queima será uma fracção f da massa total da estrela.
E = f M c2 where
| where | E | == | energia produzida por H burning |
| f | = | fracção de massa convertido em energia | |
| M | ==/td> | massa da estrela | |
| c | = | velocidade da luz |
Combinando as duas últimas equações, temos a seguinte expressão para a vida útil da sequência principal:
tMS ∼ M/L
Utilizando a relação massa-luminosidade para estrelas da sequência principal:
L ∼ M3.5
e substituindo L, temos a expressão para a duração da sequência principal em termos de massa estelar:
tMS ∼ M-2.5
Isto pode ser expresso (como acima) em unidades solares:
![]()
| where | t⊙ | == | Sun MS lifetime = 1010 |
| M | == | massa de estrela | |
| M⊙ | ==/td>> massa solar |
Nota: esta expressão é apenas uma aproximação, e não é válida para estrelas muito maciças ou muito leves. A principal limitação é a utilização da relação massa-luminosidade de valor único para estrelas de sequência principal.