Il prossimo: 8.5 Cicli Rankine Up: 8. Cicli di potenza con Previous: 8.3 Il ciclo di Carnot Contents Index
Finora abbiamo considerato solo i gas ideali e vorremmo dimostrare che le proprietà ![]()
![]()
![]() , ecc. sono vere variabili di stato e che la prima e la seconda legge della termodinamica sono valide quando il mezzo di lavoro non è un gas ideale (cioè un mezzo bifase). Un modo elegante per fare questo è considerare un ciclo di Carnot per un mezzo bifase. Affermare il fatto che tutti i motori di Carnot azionati tra due temperature date hanno la stessa efficienza è un modo di affermare la 2a legge della termodinamica. Il fluido di lavoro non deve necessariamente essere un gas ideale e può essere un mezzo bifase che cambia fase.
, ecc. sono vere variabili di stato e che la prima e la seconda legge della termodinamica sono valide quando il mezzo di lavoro non è un gas ideale (cioè un mezzo bifase). Un modo elegante per fare questo è considerare un ciclo di Carnot per un mezzo bifase. Affermare il fatto che tutti i motori di Carnot azionati tra due temperature date hanno la stessa efficienza è un modo di affermare la 2a legge della termodinamica. Il fluido di lavoro non deve necessariamente essere un gas ideale e può essere un mezzo bifase che cambia fase.
L’idea è di far funzionare un motore Carnot tra le temperature ![]() e
e![]() per un mezzo bifase e di fargli subire un cambiamento di fase. Possiamo quindi ricavare un’importante relazione nota come equazione di Clausius-Clapeyron, che dà la pendenza della curva della pressione di vapore. Potremmo quindi misurare la curva di pressione di vapore per varie sostanze e confrontare la pendenza misurata con l’equazione di Clausius-Clapeyron. Questo può essere visto come una prova sperimentale della validità generale della prima e seconda legge della termodinamica!
per un mezzo bifase e di fargli subire un cambiamento di fase. Possiamo quindi ricavare un’importante relazione nota come equazione di Clausius-Clapeyron, che dà la pendenza della curva della pressione di vapore. Potremmo quindi misurare la curva di pressione di vapore per varie sostanze e confrontare la pendenza misurata con l’equazione di Clausius-Clapeyron. Questo può essere visto come una prova sperimentale della validità generale della prima e seconda legge della termodinamica!
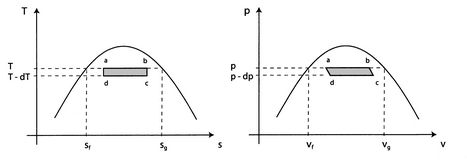
Consideriamo il ciclo infinitesimale di Carnot ![]() mostrato inFigura 8.8. Il calore viene assorbito tra gli stati
mostrato inFigura 8.8. Il calore viene assorbito tra gli stati ![]() e
e ![]() . Per vaporizzare una quantità arbitraria di massa,
. Per vaporizzare una quantità arbitraria di massa, ![]() , la quantità di calore
, la quantità di calore
| (8..1) |
deve essere fornito al sistema. Dalla prima e dalla seconda legge della termodinamica, l’efficienza termica di un ciclo di Carnot può essere scritta come
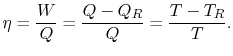 |
Quindi, per il ciclo infinitesimale considerato sopra,
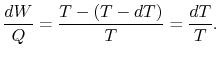 |
(8..2) |
I lavori lungo ![]() e
e ![]() quasi si annullano in modo tale che il lavoro netto è la differenza tra il lavoro lungo
quasi si annullano in modo tale che il lavoro netto è la differenza tra il lavoro lungo ![]() e
e ![]() , e
, e ![]() può essere visto come l’area racchiusa dal rettangolo
può essere visto come l’area racchiusa dal rettangolo ![]() :
:
| (8..3) |
Sostituendo le equazioni (8..1) e (8.3) in (8.2) oneobtains
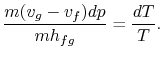 |
Riadattando i termini si ottiene l’equazione di Clausius-Clapeyron,che definisce la pendenza della curva della pressione di vapore:
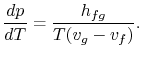 |
(8..4) |
Il bello è che abbiamo trovato una relazione generale tra le quantità misurabili sperimentalmente dai primi principi (1a e 2a legge della termodinamica).
Per tracciare la relazione Clausius-Clapeyron e confrontarla con le curve di pressione di vapore misurate sperimentalmente, dobbiamo integrare l’equazione (8.4). Per farlo, il calore di vaporizzazione e i volumi specifici devono essere funzioni note della temperatura. Questo è un problema importante in chimica fisica, ma non lo seguiremo ulteriormente qui, tranne che per menzionare che se
- le variazioni nel calore di vaporizzazione possono essere trascurate,
- la fase di vapore si assume essere un gas ideale, e
- il volume specifico del liquido è piccolo rispetto a quello della fase vapore,
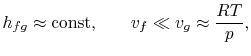 |
l’integrazione può essere facilmente realizzata8.1. Facendo queste approssimazioni, l’equazione di Clausius-Clapeyronequazione diventa
 |
Seguendo l’integrazione, l’espressione risultante è
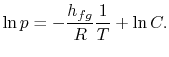 |
Nota che le curve della pressione di vapore sono linee rette se ![]() è tracciato rispetto a
è tracciato rispetto a ![]() e che la pendenza delle curve è
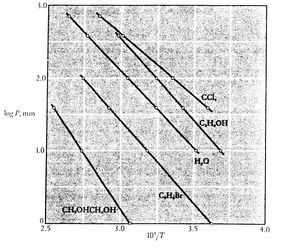
e che la pendenza delle curve è![]() , direttamente correlata al calore di vaporizzazione.Le figure 8.9, 8.9 e 8.22 mostrano le curve della pressione di vapore per varie sostanze. Il fatto che tutte le sostanze conosciute nella regione bifase soddisfino l’equazione di Clausius-Clapeyron fornisce la validità generale della prima e della seconda legge della termodinamica!
, direttamente correlata al calore di vaporizzazione.Le figure 8.9, 8.9 e 8.22 mostrano le curve della pressione di vapore per varie sostanze. Il fatto che tutte le sostanze conosciute nella regione bifase soddisfino l’equazione di Clausius-Clapeyron fornisce la validità generale della prima e della seconda legge della termodinamica!

Il prossimo: 8.5 Cicli di potenza Rankine Su: 8. Cicli di potenza con Precedente: 8.3 Il ciclo di Carnot Indice dei contenuti
UnifiedTP