Un algoritmo dividi e conquista è una strategia per risolvere un grande problema
- scomponendo il problema in sottoproblemi più piccoli
- risolvendo i sottoproblemi, e
- combinandoli per ottenere il risultato desiderato.
Per usare l’algoritmo dividi e conquista, si usa la ricorsione. Impara la ricorsione in diversi linguaggi di programmazione:
- Ricorsione in Java
- Ricorsione in Python
- Ricorsione in C++
Come funzionano gli algoritmi di divisione e conquista?
Questi sono i passi coinvolti:
- Dividi: Dividere il problema dato in sottoproblemi usando la ricorsione.
- Conquistare: Risolvere ricorsivamente i sottoproblemi più piccoli. Se il sottoproblema è abbastanza piccolo, allora risolvilo direttamente.
- Combina: Combina le soluzioni dei sottoproblemi che fanno parte del processo ricorsivo per risolvere il problema vero e proprio.
Comprendiamo questo concetto con l’aiuto di un esempio.
Qui, ordineremo un array usando l’approccio divide et impera (ie.
- Lasciamo che l’array dato sia:

Array per l’ordine di unione - Dividiamo l’array in due metà.

Dividere l’array in due sottoparti Ancora una volta, dividere ricorsivamente ogni sottoparte in due metà fino ad ottenere elementi singoli.
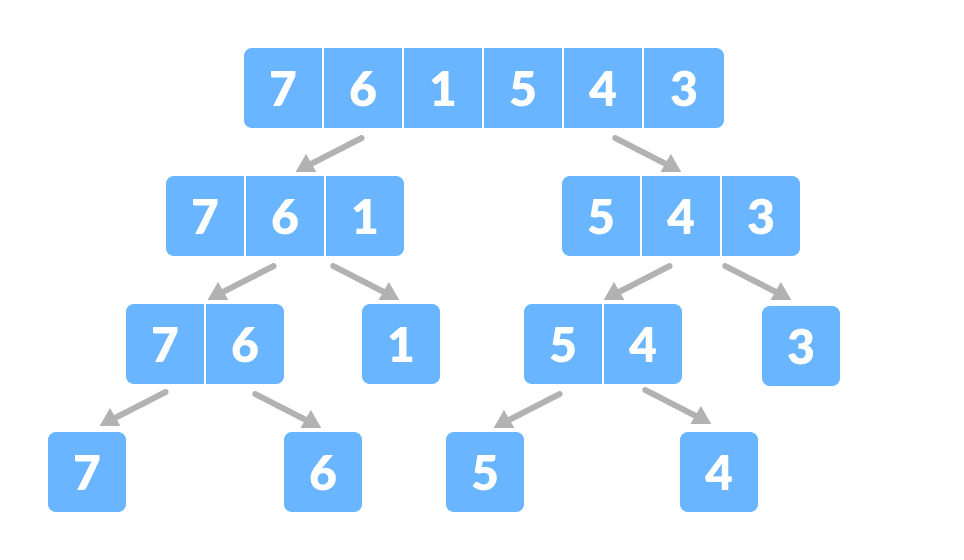
Dividete l’array in sottoparti più piccole - Ora, combinate i singoli elementi in modo ordinato. Qui, i passi di conquista e di combinazione vanno fianco a fianco.
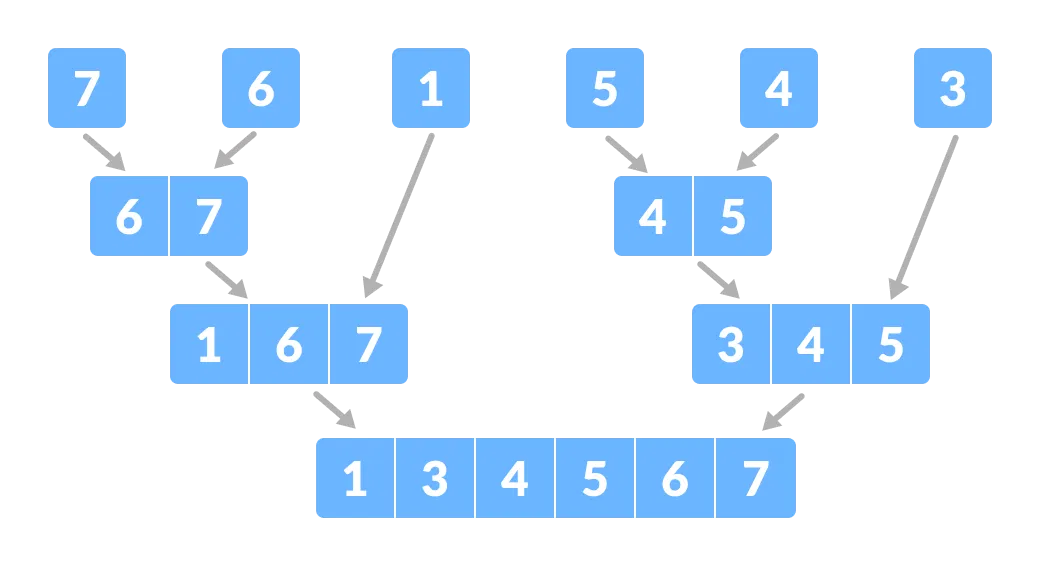
Combina le sottoparti
Complessità temporale
La complessità dell’algoritmo divide et impera è calcolata usando il teorema maestro.
T(n) = aT(n/b) + f(n),where,n = size of inputa = number of subproblems in the recursionn/b = size of each subproblem. All subproblems are assumed to have the same size.f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions
Facciamo un esempio per trovare la complessità temporale di un problema ricorsivo.
Per un ordinamento di unione, l’equazione può essere scritta come:
T(n) = aT(n/b) + f(n) = 2T(n/2) + O(n)Where, a = 2 (each time, a problem is divided into 2 subproblems)n/b = n/2 (size of each sub problem is half of the input)f(n) = time taken to divide the problem and merging the subproblemsT(n/2) = O(n log n) (To understand this, please refer to the master theorem.)Now, T(n) = 2T(n log n) + O(n) ≈ O(n log n)
Dividere e conquistare Vs approccio dinamico
L’approccio divide e conquista divide un problema in sottoproblemi più piccoli; questi sottoproblemi sono ulteriormente risolti in modo ricorsivo. Il risultato di ogni sottoproblema non viene memorizzato per riferimento futuro, mentre, in un approccio dinamico, il risultato di ogni sottoproblema viene memorizzato per riferimento futuro.
Utilizzare l’approccio divide et impera quando lo stesso sottoproblema non viene risolto più volte. Utilizzare l’approccio dinamico quando il risultato di un sottoproblema deve essere usato più volte in futuro.
Comprendiamo questo con un esempio. Supponiamo di voler trovare la serie di Fibonacci. Allora,
Approccio dividi e conquista:
fib(n) If n < 2, return 1 Else , return f(n - 1) + f(n -2)
Approccio dinamico:
mem = fib(n) If n in mem: return mem else, If n < 2, f = 1 else , f = f(n - 1) + f(n -2) mem = f return f
In un approccio dinamico, mem memorizza il risultato di ogni sottoproblema.
Svantaggi dell’algoritmo Dividi e Conquista
- La complessità per la moltiplicazione di due matrici usando il metodo ingenuo è O(n3), mentre usando l’approccio dividi e conquista (cioè la moltiplicazione della matrice di Strassen) è O(n2.8074). Questo approccio semplifica anche altri problemi, come la Torre di Hanoi.
- Questo approccio è adatto a sistemi multiprocesso.
- Fa un uso efficiente delle cache di memoria.
Applicazioni dividi e conquista
- Ricerca binaria
- Merge Sort
- Quick Sort
- Moltiplicazione della matrice di Strassen
- Algoritmo Karatsuba



