Heading

In meinem ersten Beitrag über neuronale Netzwerke habe ich eine Modelldarstellung für neuronale Netzwerke besprochen und wie wir Eingaben einspeisen und eine Ausgabe berechnen können. Wir haben diese Ausgabe Schicht für Schicht berechnet, indem wir die Eingaben aus der vorherigen Schicht mit den Gewichten für jede Neuron-Neuron-Verbindung kombiniert haben. Ich erwähnte, dass wir in einem zukünftigen Beitrag darüber sprechen würden, wie man die richtigen Gewichte für die Verbindung der Neuronen untereinander findet – dies ist dieser Beitrag!

Übersicht

Im vorherigen Beitrag hatte ich einfach angenommen, dass wir magisches Vorwissen über die richtigen Gewichte für jedes neuronale Netz haben. In diesem Beitrag werden wir tatsächlich herausfinden, wie wir unser neuronales Netz dazu bringen, die richtigen Gewichte zu „lernen“. Um jedoch einen Ansatzpunkt zu haben, werden wir die Gewichte zunächst mit zufälligen Werten initialisieren, um eine erste Vermutung anzustellen. Wir werden diesen Schritt der zufälligen Initialisierung später in diesem Beitrag noch einmal aufgreifen.

Mit den zufällig initialisierten Gewichten, die jedes Neuron verbinden, können wir nun unsere Beobachtungsmatrix einspeisen und die Ausgaben unseres neuronalen Netzwerks berechnen. Dies wird als Vorwärtspropagation bezeichnet. Da wir unsere Gewichte zufällig gewählt haben, wird unsere Ausgabe wahrscheinlich nicht sehr gut sein, was die erwartete Ausgabe für den Datensatz betrifft.

Wie geht es also weiter?

Zunächst sollten wir definieren, wie eine „gute“ Ausgabe aussieht. Wir werden nämlich eine Kostenfunktion entwickeln, die Ausgaben bestraft, die weit vom erwarteten Wert entfernt sind.

Als Nächstes müssen wir einen Weg finden, die Gewichte so zu ändern, dass sich die Kostenfunktion verbessert. Jeder gegebene Pfad von einem Eingangsneuron zu einem Ausgangsneuron ist im Wesentlichen nur eine Komposition von Funktionen; als solche können wir partielle Ableitungen und die Kettenregel verwenden, um die Beziehung zwischen jedem gegebenen Gewicht und der Kostenfunktion zu definieren. Mit diesem Wissen können wir dann den Gradientenabstieg bei der Aktualisierung der einzelnen Gewichte nutzen.

Voraussetzungen

Als ich zum ersten Mal Backpropagation lernte, versuchten viele Leute, die zugrundeliegende Mathematik (Ableitungsketten) zu abstrahieren, und ich war nie wirklich in der Lage zu begreifen, was da eigentlich vor sich ging, bis ich Professor Winstons Vorlesung am MIT sah. Ich hoffe, dass dieser Beitrag ein besseres Verständnis von Backpropagation vermittelt als nur „das ist der Schritt, bei dem wir den Fehler zurückschicken, um die Gewichte zu aktualisieren“.

Um die in diesem Beitrag besprochenen Konzepte vollständig zu verstehen, sollten Sie mit den folgenden Dingen vertraut sein:

Partielle Ableitungen
Dieser Beitrag wird ein bisschen dicht sein mit einer Menge partieller Ableitungen. Ich hoffe jedoch, dass auch ein Leser ohne Vorkenntnisse der multivariaten Kalkulation der Logik hinter der Backpropagation folgen kann.

Wenn Sie mit der Kalkulation nicht vertraut sind, wird $\frac{{\partial f\left( x \right)}}{{{\partial x}}$ wahrscheinlich ziemlich fremd aussehen. Sie können diesen Ausdruck interpretieren als „Wie ändert sich $f\left( x \right)$, wenn ich $x$ ändere?“ Dies ist nützlich, weil wir Fragen stellen können wie „Wie ändert sich die Kostenfunktion, wenn ich diesen Parameter ändere? Erhöht oder verringert sich die Kostenfunktion?“ auf der Suche nach den optimalen Parametern.

Wenn Sie Ihre Kenntnisse in multivariater Infinitesimalrechnung auffrischen möchten, schauen Sie sich die Lektionen von Khan Academy zu diesem Thema an.

Gradientenabstieg
Um diesen Beitrag nicht zu lang werden zu lassen, habe ich das Thema Gradientenabstieg in einen weiteren Beitrag aufgeteilt. Wenn Sie mit der Methode nicht vertraut sind, sollten Sie sie hier nachlesen und verstehen, bevor Sie diesen Beitrag fortsetzen.

Matrixmultiplikation
Hier ist eine kurze Auffrischung von Khan Academy.

Einfach anfangen

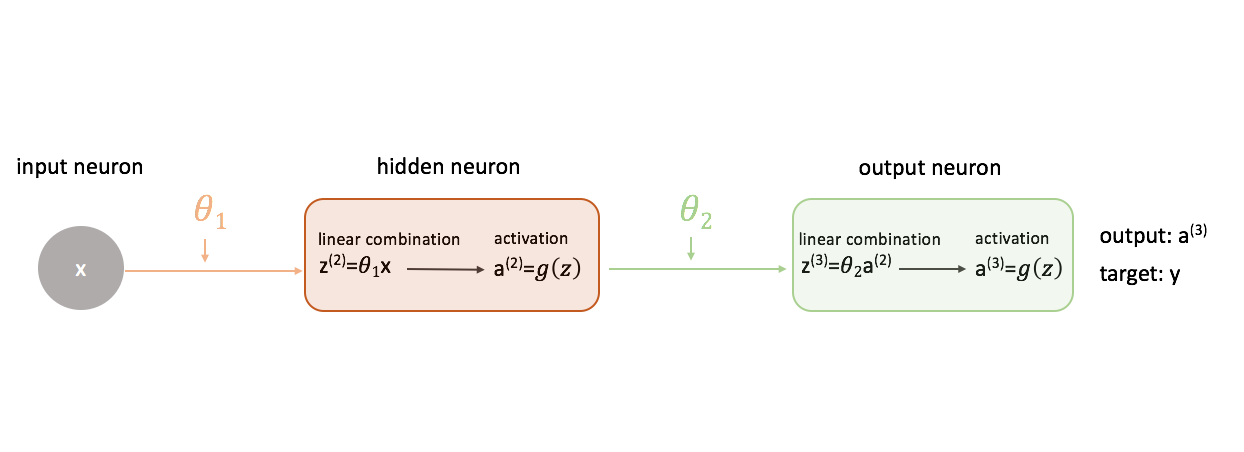
Um herauszufinden, wie man den Gradientenabstieg beim Training eines neuronalen Netzes verwendet, beginnen wir mit dem einfachsten neuronalen Netz: ein Eingabeneuron, ein Neuron der versteckten Schicht und ein Ausgabeneuron.

Um ein vollständigeres Bild zu zeigen, was vor sich geht, habe ich jedes Neuron erweitert, um 1) die lineare Kombination von Eingaben und Gewichten und 2) die Aktivierung dieser linearen Kombination zu zeigen. Es ist leicht zu erkennen, dass der Schritt der Vorwärtspropagation einfach eine Reihe von Funktionen ist, wobei die Ausgabe einer Funktion als Eingabe für die nächste dient.

Definieren einer „guten“ Leistung in einem neuronalen Netzwerk

Lassen Sie uns unsere Kostenfunktion einfach als den quadrierten Fehler definieren.

Es gibt eine Unzahl von Kostenfunktionen, die wir verwenden könnten, aber für dieses neuronale Netzwerk wird der quadrierte Fehler gut funktionieren.

Erinnern Sie sich daran, dass wir die Ausgabe unseres Modells in Bezug auf die Zielausgabe bewerten wollen, um die Differenz zwischen den beiden zu minimieren.

Beziehung der Gewichte zur Kostenfunktion

Um die Differenz zwischen der Ausgabe unseres neuronalen Netzwerks und der Zielausgabe zu minimieren, müssen wir wissen, wie sich die Modellleistung in Bezug auf jeden Parameter in unserem Modell ändert. Mit anderen Worten, wir müssen die Beziehung (sprich: die partielle Ableitung) zwischen unserer Kostenfunktion und jedem Gewicht definieren. Dann können wir diese Gewichte in einem iterativen Prozess unter Verwendung des Gradientenabstiegs aktualisieren.

Lassen Sie uns zunächst $\frac{{\partial J\left( \theta \right)}}{{\partial {\theta _2}}}$ betrachten. Behalten Sie die folgende Abbildung im Hinterkopf, während wir fortfahren.

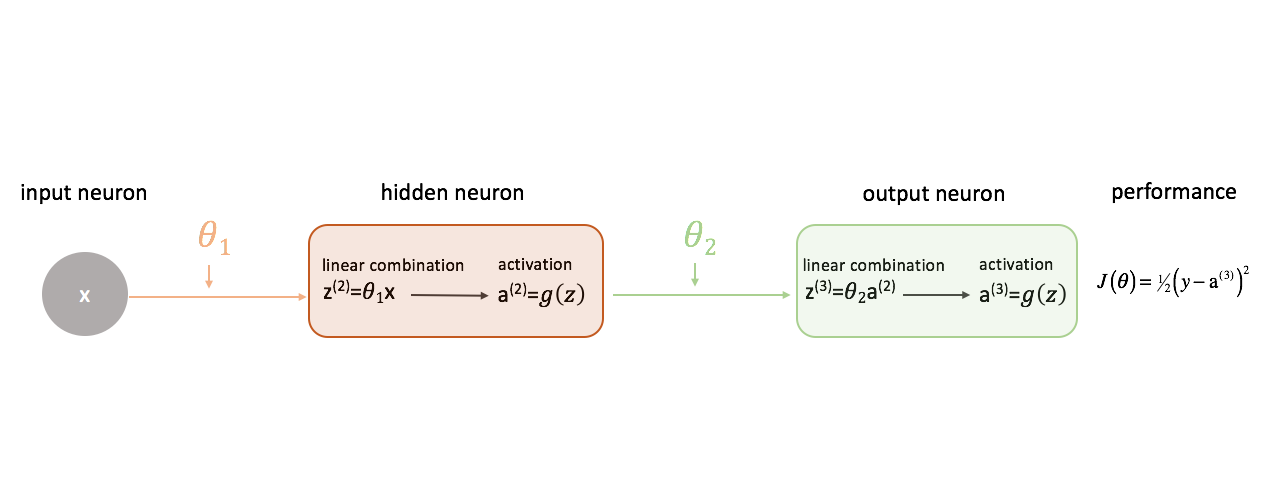
Lassen Sie uns einen Moment untersuchen, wie wir die Beziehung zwischen $J\left( \theta \right)$ und $\theta _2$ ausdrücken könnten. Beachten Sie, dass $\theta _2$ eine Eingabe für ${z^{(3)}}$ ist, die eine Eingabe für ${{\rm{a}}^{(3)}}$ ist, die eine Eingabe für $J\left( \theta \right)$ ist. Wenn wir versuchen, eine Ableitung dieser Art zu berechnen, können wir die Kettenregel zur Lösung verwenden.

Zur Erinnerung, die Kettenregel besagt:

Lassen Sie uns die Kettenregel anwenden, um $\frac{{\partial J\left( \theta \right)}}{{{\partial {\theta _2}}$ zu lösen.

Mit einer ähnlichen Logik können wir $\frac{{\partial J\left( \theta \right)}}{{\partial {\theta _1}}$ finden.

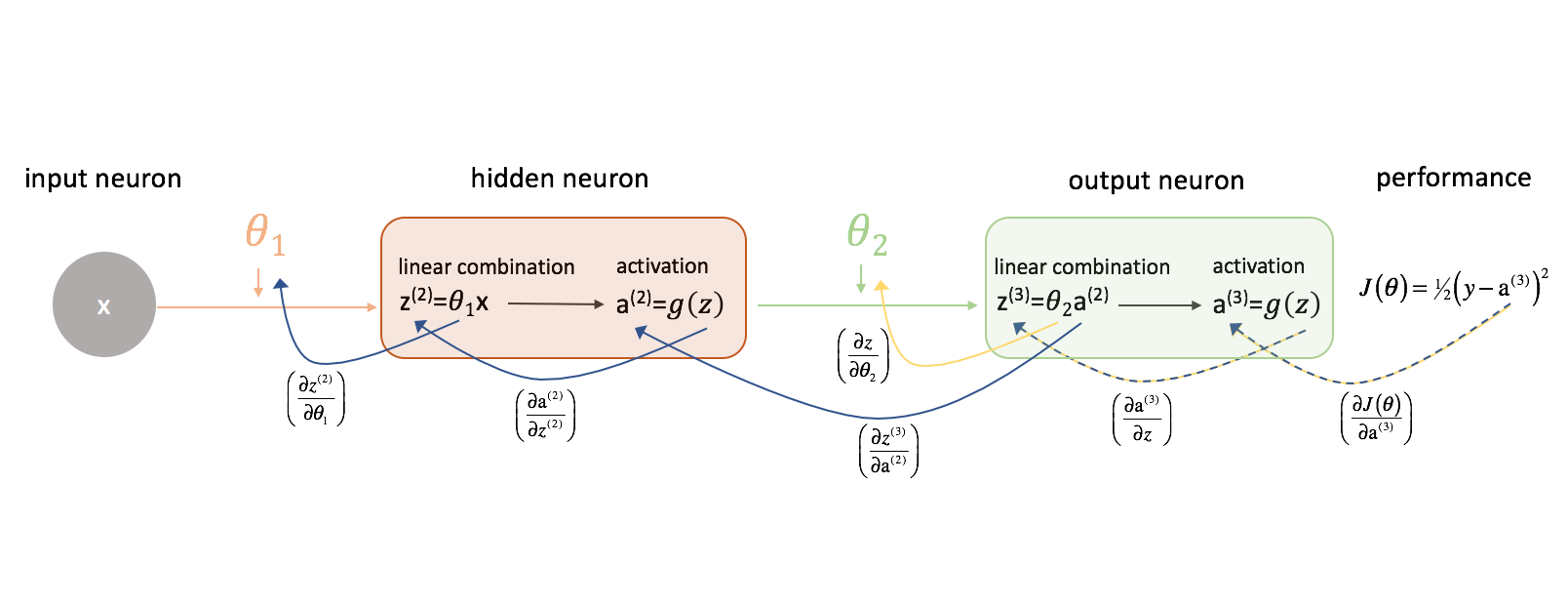
Der Übersichtlichkeit halber habe ich unser Diagramm des neuronalen Netzes aktualisiert, um diese Ketten zu visualisieren. Stellen Sie sicher, dass Sie mit diesem Prozess vertraut sind, bevor Sie fortfahren.

Komplexität hinzufügen

Nun wollen wir den gleichen Ansatz an einem etwas komplizierteren Beispiel ausprobieren. Jetzt betrachten wir ein neuronales Netzwerk mit zwei Neuronen in der Eingabeschicht, zwei Neuronen in einer versteckten Schicht und zwei Neuronen in der Ausgabeschicht. Die Bias-Neuronen, die in der Eingabe- und der versteckten Schicht fehlen, lassen wir vorerst außer Acht.

Lassen Sie uns kurz die Notation durchgehen, die ich verwenden werde, damit Sie den Diagrammen folgen können. Die hochgestellte Zahl (1) gibt an, in welcher Schicht sich das Objekt befindet und die tiefgestellte Zahl gibt an, auf welches Neuron wir uns in einer bestimmten Schicht beziehen. Zum Beispiel ist $a_1^{(2)}$ die Aktivierung des ersten Neurons in der zweiten Schicht. Die Parameterwerte $\theta$ lese ich gerne wie ein Versandetikett – der erste Wert gibt an, zu welchem Neuron in der nächsten Schicht die Eingabe gesendet wird, und der zweite Wert gibt an, von welchem Neuron die Information gesendet wird. Zum Beispiel wird ${\theta _{21}^{(2)}}$ verwendet, um eine Eingabe an das 2. Neuron zu senden, vom 1. Neuron in Schicht 2. Die hochgestellte Zahl, die die Schicht bezeichnet, entspricht der Stelle, von der die Eingabe kommt. Diese Notation ist konsistent mit der Matrixdarstellung, die wir in meinem Beitrag über die Darstellung neuronaler Netze besprochen haben.

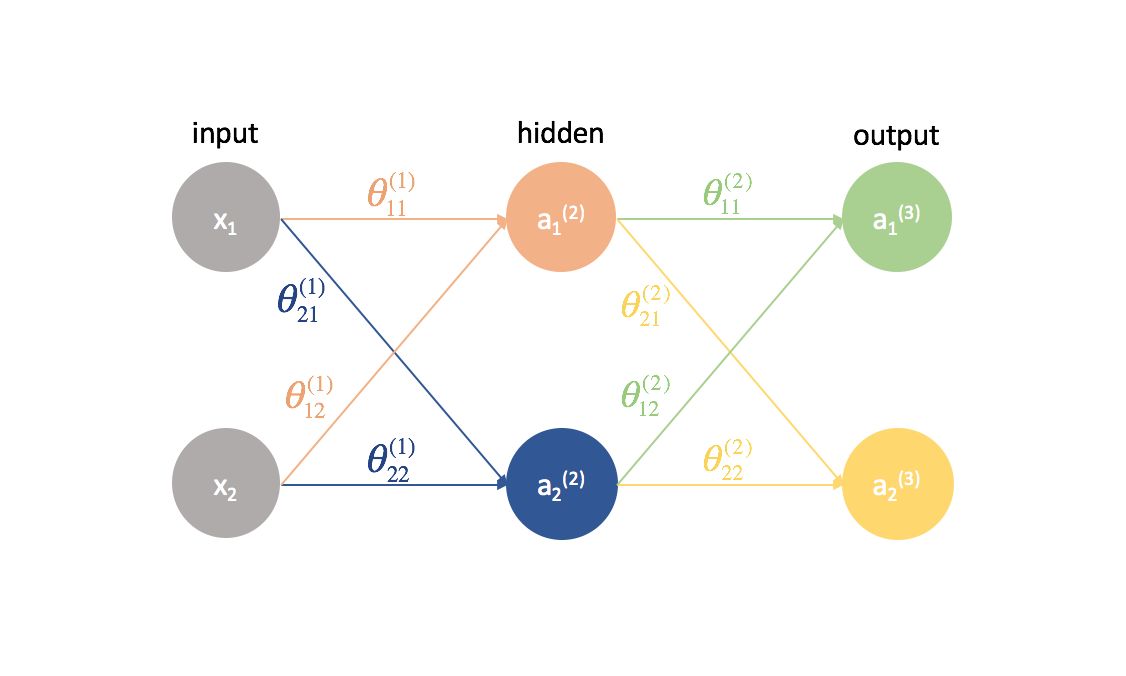
Lassen Sie uns dieses Netzwerk erweitern, um die ganze Mathematik, die hier vor sich geht, zu zeigen.

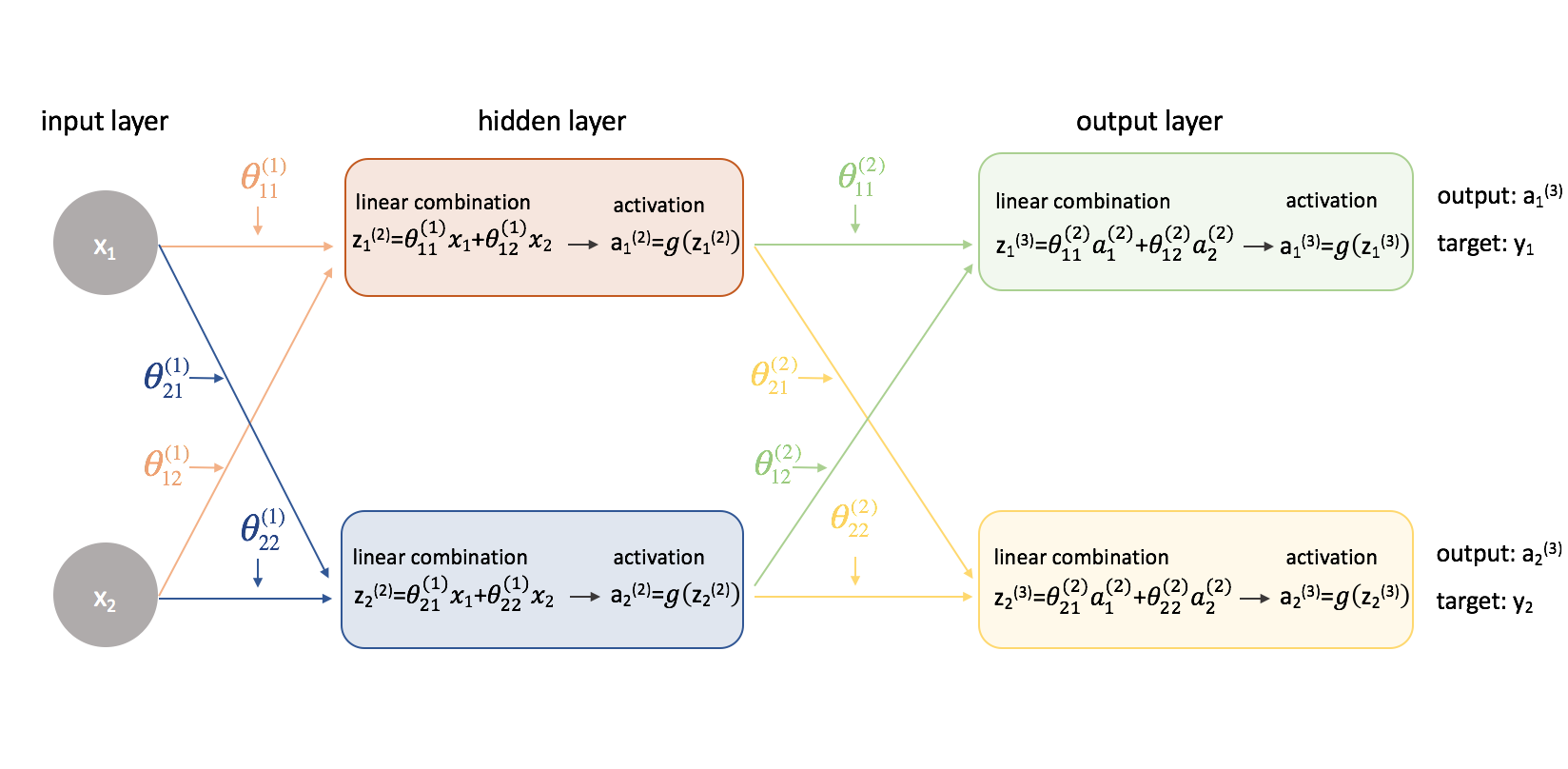
Huch! Die Dinge sind ein wenig komplizierter geworden. Ich werde den Prozess zum Finden einer der partiellen Ableitungen der Kostenfunktion in Bezug auf einen der Parameterwerte durchgehen; den Rest der Berechnungen überlasse ich dem Leser als Übung (und poste die Endergebnisse weiter unten).

Vor allem müssen wir unsere Kostenfunktion überarbeiten, da wir es jetzt mit einem neuronalen Netzwerk mit mehr als einem Ausgang zu tun haben. Wir verwenden jetzt den mittleren quadratischen Fehler als Kostenfunktion.

Hinweis: Wenn Sie mit mehreren Beobachtungen trainieren (was Sie in der Praxis immer tun werden), müssen wir auch eine Summierung der Kostenfunktion über alle Trainingsbeispiele durchführen. Für diese Kostenfunktion ist es üblich, mit $\frac{1}{{m}}$ zu normalisieren, wobei $m$ die Anzahl der Beispiele in Ihrem Trainingsdatensatz ist.

Nachdem wir nun unsere Kostenfunktion korrigiert haben, können wir uns ansehen, wie die Änderung eines Parameters die Kostenfunktion beeinflusst. Konkret berechne ich in diesem Beispiel $\frac{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}}$. Betrachtet man das Diagramm, so wirkt sich $\theta _{11}^{(1)}$ sowohl auf die Ausgabe für $a _1^{(3)}$ als auch für $a _2^{(3)}$ aus. Da unsere Kostenfunktion eine Summierung der einzelnen Kosten für jeden Ausgang ist, können wir die Ableitungskette für jeden Pfad berechnen und sie einfach addieren.

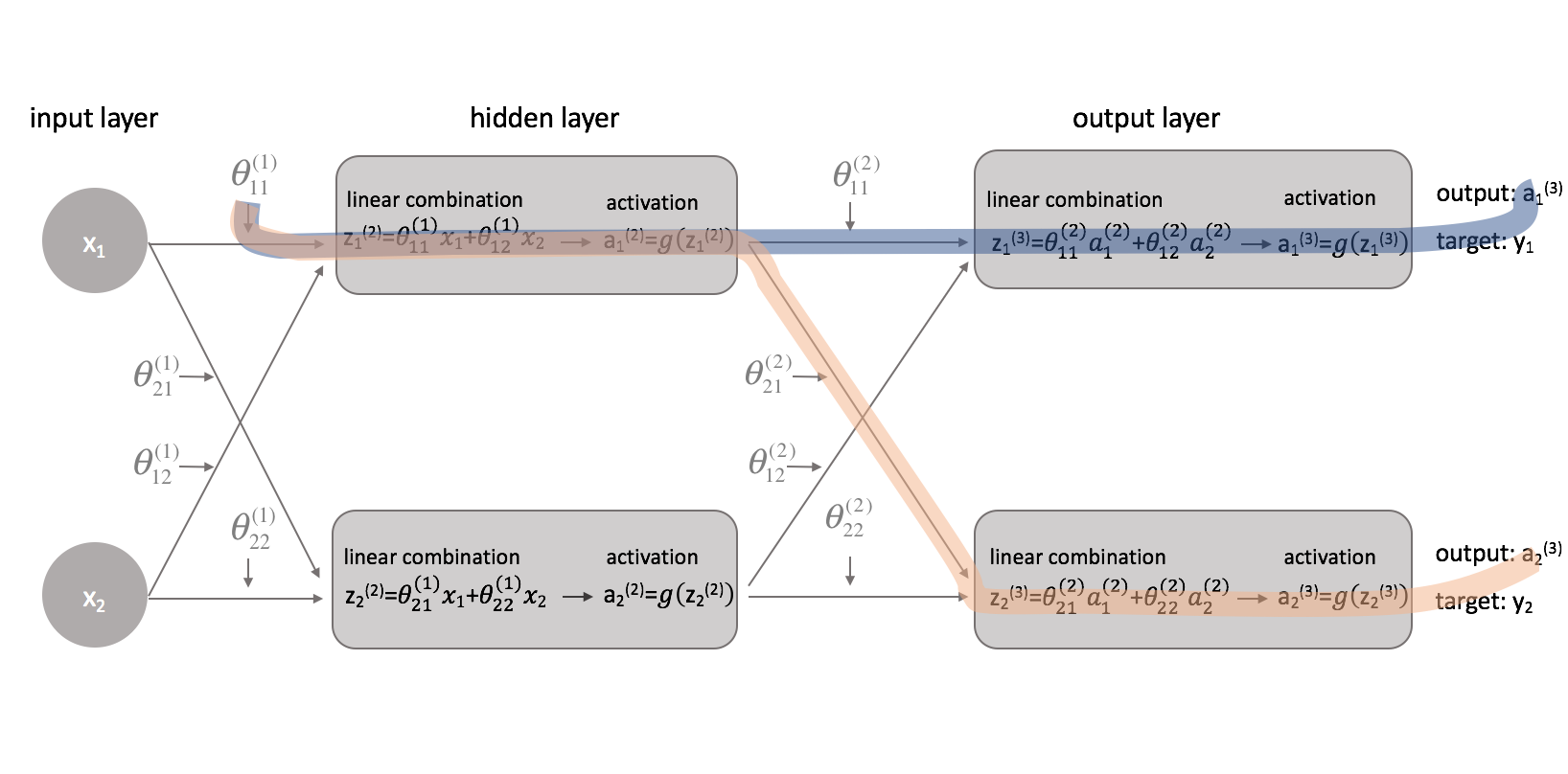
Die Ableitungskette für den blauen Pfad ist:
$ \left( {\frac{{\partial J\left( \theta \right)}}{{\partial {\rm{a}} _1^{(3)}}}} \right)\left( {\frac{{\partial {\rm{a}} _1^{(3)}}}{{\partial z _1^{(3)}}}} \right)\left( {\frac{{\partial z _1^{(3)}}}{{\partial {\rm{a}} _1^{(2)}}}} \right)\left( {\frac{{\partial {\rm{a}} _1^{(2)}}}{{\partial z _1^{(2)}}}} \rechts)\left( {\frac{{\partial z _1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \right) $

Die Ableitungskette für den orangenen Pfad lautet:
$ \left( {\frac{{\partial J\left( \theta \right)}}{{\partial {\rm{a}} _2^{(3)}}}} \right)\left( {\frac{{\partial {\rm{a}} _2^{(3)}}}{{\partial z _2^{(3)}}}} \right)\left( {\frac{{\partial z _2^{(3)}}}{{\partial {\rm{a}} _1^{(2)}}}} \right)\left( {\frac{{\partial {\rm{a}} _1^{(2)}}}{{\partial z _1^{(2)}}}} \right)\left( {\frac{{\partial z _1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \theta \right)$

Kombiniert man diese, erhält man den Gesamtausdruck für $\frac{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}}$.

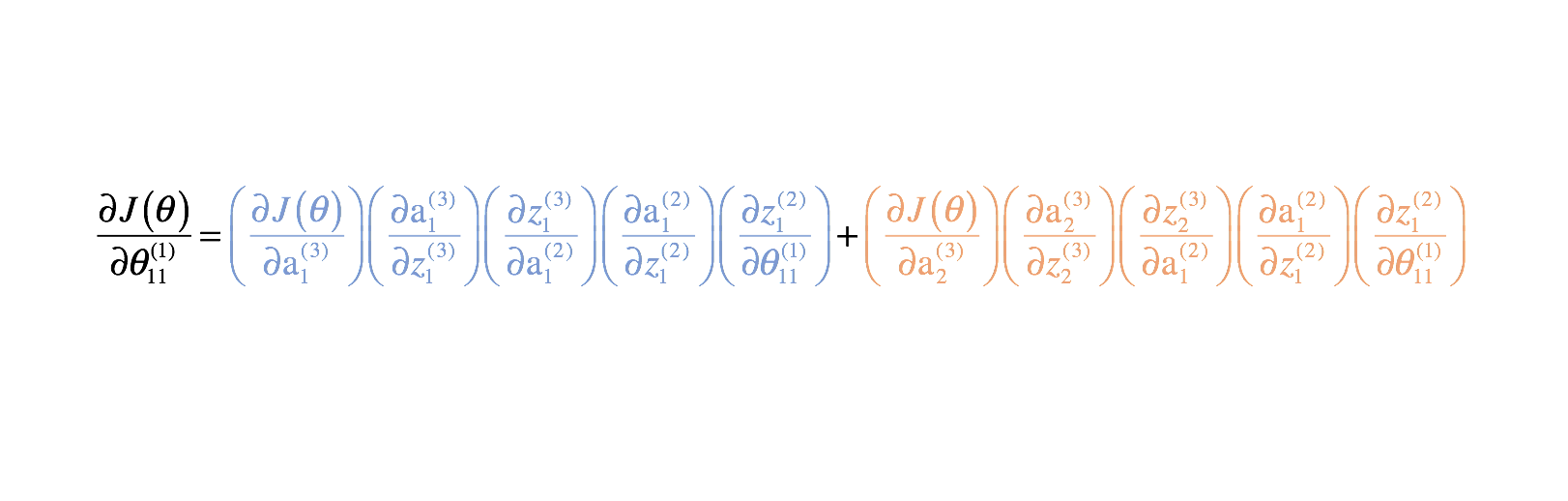
Ich habe den Rest der partiellen Ableitungen unten angegeben. Denken Sie daran, dass wir diese partiellen Ableitungen brauchen, weil sie beschreiben, wie die Änderung jedes Parameters die Kostenfunktion beeinflusst. Auf diese Weise können wir dieses Wissen nutzen, um alle Parameterwerte so zu ändern, dass die Kostenfunktion weiter sinkt, bis wir auf einen Minimalwert konvergieren.

Schicht-2-Parameter

Schicht-1-Parameter

Da. Wir sind gerade von einem neuronalen Netz mit 2 Parametern, das im vorherigen Beispiel 8 partielle Ableitungsterme benötigte, zu einem neuronalen Netz mit 8 Parametern übergegangen, das 52 partielle Ableitungsterme benötigt. Das kann schnell aus dem Ruder laufen, vor allem wenn man bedenkt, dass viele neuronale Netze, die in der Praxis verwendet werden, viel größer sind als diese Beispiele.

Glücklicherweise wiederholen sich bei näherer Betrachtung viele dieser partiellen Ableitungen. Wenn wir dieses Problem geschickt angehen, können wir den Rechenaufwand für das Training drastisch reduzieren. Außerdem wäre es wirklich mühsam, wenn wir die Ableitungsketten für jeden Parameter manuell berechnen müssten. Schauen wir uns an, was wir bisher gemacht haben und sehen wir, ob wir eine Methode für diesen Wahnsinn verallgemeinern können.

Verallgemeinerung einer Methode

Lassen Sie uns die obigen partiellen Ableitungen untersuchen und ein paar Beobachtungen machen. Wir beginnen mit der Betrachtung der partiellen Ableitungen in Bezug auf die Parameter für Schicht 2. Denken Sie daran, dass die Parameter für Schicht 2 mit den Aktivierungen in Schicht 2 kombiniert werden, um als Eingaben in Schicht 3 zu dienen.

Schicht-2-Parameter

Lassen Sie uns die folgenden Ausdrücke analysieren; ich ermutige Sie, die partiellen Ableitungen nach und nach zu lösen, um sich von meiner Logik zu überzeugen.

Zunächst scheint es, als ob die Spalten sehr ähnliche Werte enthalten. Zum Beispiel enthält die erste Spalte partielle Ableitungen der Kostenfunktion in Bezug auf die Ausgaben des neuronalen Netzes. In der Praxis ist dies die Differenz zwischen der erwarteten Ausgabe und der tatsächlichen Ausgabe (und dann skaliert mit $m$) für jedes der Ausgangsneuronen.

Die zweite Spalte stellt die Ableitung der Aktivierungsfunktion dar, die in der Ausgangsschicht verwendet wird. Beachten Sie, dass die Neuronen in jeder Schicht die gleiche Aktivierungsfunktion verwenden. Eine homogene Aktivierungsfunktion innerhalb einer Schicht ist notwendig, um die Matrixoperationen bei der Berechnung der Ausgabe des neuronalen Netzes nutzen zu können. Der Wert für die zweite Spalte wird also für alle vier Terme gleich sein.

Die erste und zweite Spalte können der Einfachheit halber später als $\delta _i^{(3)}$ zusammengefasst werden. Es ist nicht sofort ersichtlich, warum dies hilfreich ist, aber Sie werden im weiteren Verlauf sehen, warum dies sinnvoll ist. Man wird diesen Ausdruck oft als „Fehler“-Term bezeichnen, den wir verwenden, um „Fehler vom Ausgang durch das gesamte Netzwerk zurückzuschicken“. Wir werden gleich sehen, warum dies der Fall ist. Jedes Neuron im Netz hat einen entsprechenden $\delta$-Term, den wir lösen werden.

Die dritte Spalte stellt dar, wie sich der interessierende Parameter in Bezug auf die gewichteten Eingänge für die aktuelle Schicht ändert; wenn Sie die Ableitung berechnen, entspricht dies der Aktivierung aus der vorherigen Schicht.

Zudem möchte ich anmerken, dass die ersten beiden partiellen Ableitungsterme sich auf das erste Ausgangsneuron (Neuron 1 in Schicht 3) zu beziehen scheinen, während die letzten beiden partiellen Ableitungsterme sich auf das zweite Ausgangsneuron (Neuron 2 in Schicht 3) zu beziehen scheinen. Dies ist in dem Term $\frac{{\partial J\left( \theta \right)}}{{\partial {\rm{a}}_i^{(3)}}$ ersichtlich. Nutzen wir dieses Wissen, um die partiellen Ableitungen mit Hilfe des oben definierten Ausdrucks $\delta$ umzuschreiben.

Als Nächstes machen wir weiter und berechnen den letzten Term der partiellen Ableitung. Wie wir festgestellt haben, repräsentiert diese partielle Ableitung am Ende die Aktivierungen der vorherigen Schicht.

Hinweis: Ich finde es hilfreich, bei der Berechnung der partiellen Ableitungen die erweiterte Grafik des neuronalen Netzes aus dem vorherigen Abschnitt zu verwenden.

Es scheint, dass wir die „Fehler“-Terme mit den Aktivierungen aus der vorherigen Schicht kombinieren, um jede partielle Ableitung zu berechnen. Es ist auch interessant, dass die Indizes $j$ und $k$ für $\theta _{jk}$ mit den kombinierten Indizes von $\delta _j^{(3)}$ und ${\rm{a}} _k^{(2)}$.

Lassen Sie uns sehen, ob wir eine Matrixoperation finden können, um alle partiellen Ableitungen in einem Ausdruck zu berechnen.

${\delta ^{(3)}}$ ist ein Vektor der Länge $j$, wobei $j$ gleich der Anzahl der Ausgangsneuronen ist.

δ (3) = f ′ ( a (3) )

${\rm{a}}^{(2)}$ ist ein Vektor der Länge $k$, wobei $k$ die Anzahl der Neuronen in der vorherigen Schicht ist. Die Werte dieses Vektors repräsentieren die Aktivierungen der vorhergehenden Schicht, die während der Vorwärtspropagation berechnet wurden; mit anderen Worten, es ist der Vektor der Eingänge zur Ausgabeschicht.

$ {a^{(2)}} = \left $

Multipliziert man diese Vektoren miteinander, kann man alle partiellen Ableitungsterme in einem Ausdruck berechnen.

∂J( θ ) ∂ θ ij (2) ==

Zusammenfassend siehe die folgende Grafik.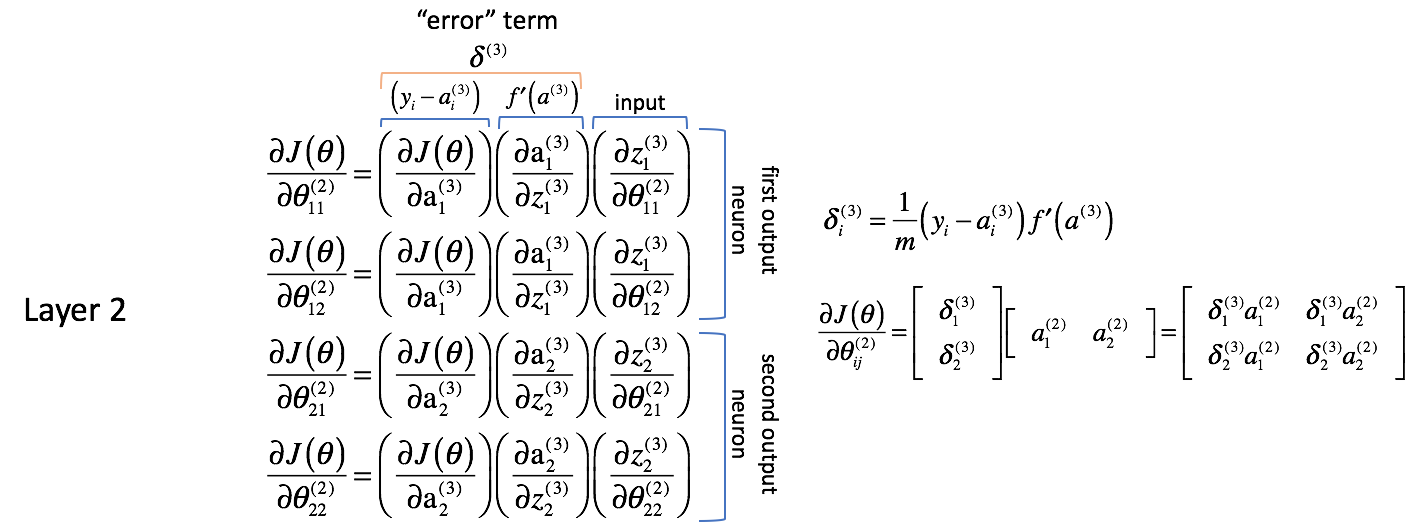

Anmerkung: Technisch gesehen müsste die erste Spalte auch nach $m$ skaliert werden, um eine genaue Ableitung zu erhalten. Mir ging es jedoch darum, darauf hinzuweisen, dass es sich hier um die Spalte handelt, in der es um die Differenz zwischen dem erwarteten und dem tatsächlichen Ausgang geht. Der Term $\delta$ auf der rechten Seite hat den vollen Ableitungsausdruck.

Parameter der Schicht 1

Schauen wir uns nun an, was in Schicht 1 vor sich geht.

Während die Gewichte in Schicht 2 nur einen Ausgang direkt beeinflusst haben, beeinflussen die Gewichte in Schicht 1 alle Ausgänge. Erinnern Sie sich an die folgende Grafik.

Das führt dazu, dass eine partielle Ableitung der Kostenfunktion nach einem Parameter nun zu einer Summierung verschiedener Ketten wird. Genauer gesagt, haben wir eine Ableitungskette für jedes $\delta$, das wir in der nächsten Schicht vorwärts berechnet haben. Erinnern Sie sich daran, dass wir am Ende des Netzwerks begonnen haben und uns rückwärts durch das Netzwerk arbeiten. Die nächste Schicht vorwärts repräsentiert also die $\delta$-Werte, die wir zuvor berechnet haben.

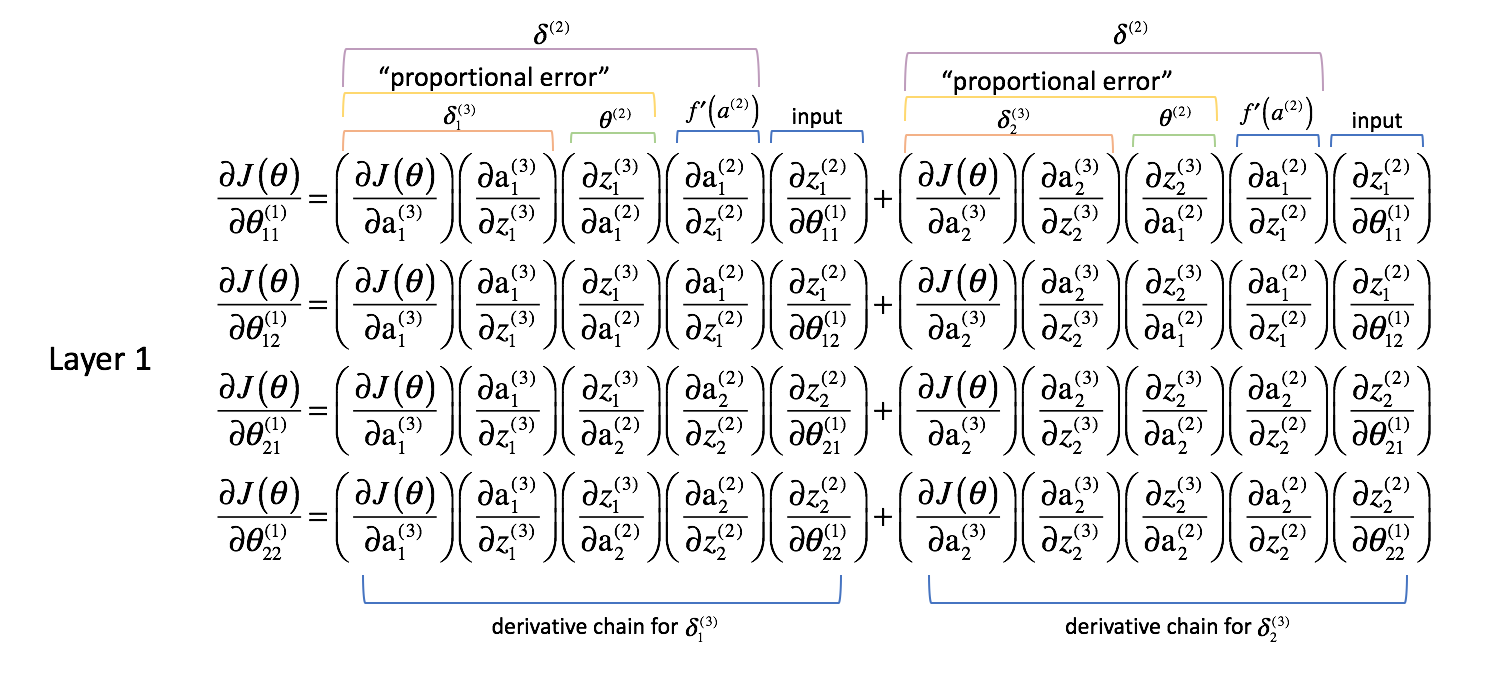
Wie wir es für Schicht 2 getan haben, wollen wir ein paar Beobachtungen machen.

Die ersten beiden Spalten (jedes summierten Terms) entsprechen einem $\delta _j^{(3)}$, das in der nächsten Schicht vorwärts berechnet wurde (denken Sie daran, wir haben am Ende des Netzwerks begonnen und arbeiten uns zurück).

Die dritte Spalte entspricht einem Parameter, der die Schicht 2 mit der Schicht 3 verbindet. Wenn wir $\delta _j^{(3)}$ als einen „Fehler“-Term für Schicht 3 betrachten, und jede Ableitungskette ist nun eine Summierung dieser Fehler, dann erlaubt uns diese dritte Spalte, jeden jeweiligen Fehler zu gewichten. Somit stellen die ersten drei Terme zusammen ein gewisses Maß des proportionalen Fehlers dar.

Wir werden auch $\delta$ für alle Schichten außer der Ausgabeschicht neu definieren, um diese Kombination gewichteter Fehler einzubeziehen.

$ \delta _j^{(l)} = f’\left( {{a^{(l)}} {{a^{(l)}}) = f’\rechts)\sum\limits _{i = 1}^n {\delta _i^{(l + 1)}\theta _{ij}^{(l)}} $

Wir könnten dies prägnanter mit Matrixausdrücken schreiben.

$ {\delta ^{(l)}} = {\delta ^{(l + 1)}}{\Theta ^{(l)}}f’\left( {{a^{(l)}}} \right) $

Hinweis: Es ist Standardnotation, Vektoren mit Kleinbuchstaben und Matrizen mit Großbuchstaben zu bezeichnen. So steht $\theta$ für einen Vektor und $\Theta$ für eine Matrix.

Die vierte Spalte stellt die Ableitung der Aktivierungsfunktion dar, die in der aktuellen Schicht verwendet wird. Denken Sie daran, dass die Neuronen in jeder Schicht die gleiche Aktivierungsfunktion verwenden.

Die fünfte Spalte schließlich repräsentiert verschiedene Eingaben aus der vorherigen Schicht. In diesem Fall handelt es sich um die tatsächlichen Eingaben in das neuronale Netz.

Schauen wir uns einen der Terme genauer an, nämlich $\frac{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}}$.

Zunächst haben wir festgestellt, dass die ersten beiden Spalten jeder Ableitungskette zuvor als $\delta _j^{(3)}$ berechnet wurden.

$ \frac{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}} = \delta _1^{(3)}\left( {\frac{{\partial z _1^{(3)}}}{{{\partial {\rm{a}} _1^{(2)}}}} \right)\left( {\frac{{\partial {\rm{a}} _1^{(2)}}}{{\partial z _1^{(2)}}}} \right)\left( {\frac{{\partial z _1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \right) + \delta _2^{(3)}\left( {\frac{{\partial z _2^{(3)}}}{{\partial {\rm{a}} _1^{(2)}}}} \right)\left( {\frac{{\partial {\rm{a}} _1^{(2)}}}{{\partial z _1^{(2)}}}} \right)\left( {\frac{{\partial z _1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \right) $

Weiterhin stellten wir fest, dass die dritte Spalte jeder Ableitungskette ein Parameter war, der zur Gewichtung jedes der jeweiligen $\delta$-Terme diente. Wir haben auch festgestellt, dass die vierte Spalte die Ableitung der Aktivierungsfunktion war.

$ \frac{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}} = \delta _1^{(3)}\theta _{11}^{(2)}f’\left( {{a^{(2)}} \right)\left( {\frac{{\partial z _1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \rechts) + \delta _2^{(3)}\theta _{21}^{(2)}f’\left( {{a^{(2)}} \right)\left( {\frac{{\partial z _1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \right) $

Faktorisierung von $\left( {\frac{{\partial z_1^{(2)}}}{{\partial \theta _{11}^{(1)}}}} \right)$,

$ \frac{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}} = \left( {\frac{{\partial z _1^{(2)}}}{{{\partial \theta _{11}^{(1)}}}} \rechts)\left( {\delta _1^{(3)}\theta _{11}^{(2)}f’\left( {{a^{(2)}} \rechts) + \delta _2^{(3)}\theta _{21}^{(2)}f’\left( {{a^{(2)}} \right)} \right) $

Wir haben nun unsere neue Definition von $\delta_j^{(l)}$. Setzen wir das ein.

$ \frac{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}} = \left( {\frac{{\partial z _1^{(2)}}}{{{\partial \theta _{11}^{(1)}}}} \right)\left( {\delta _1^{(2)}} \rechts) $

Zuletzt haben wir festgestellt, dass die fünfte Spalte (${\frac{{\partial z_1^{(2)}}}{{\partial \theta_{11}^{(1)}}}}$) einer Eingabe aus der vorherigen Schicht entspricht. In diesem Fall berechnet sich die Ableitung zu $x_1$.

$ \frac{{\partial J\left( \theta \right)}}{{\partial \theta _{11}^{(1)}} = \delta _1^{(2)}{x _1} $

Lassen Sie uns wieder eine Matrixoperation finden, um alle partiellen Ableitungen in einem Ausdruck zu berechnen.

$\delta ^{(2)}$ ist ein Vektor der Länge $j$, wobei $j$ die Anzahl der Neuronen in der aktuellen Schicht (Schicht 2) ist. Wir können $\delta ^{(2)}$ als die gewichtete Kombination der Fehler aus Schicht 3 berechnen, multipliziert mit der Ableitung der Aktivierungsfunktion, die in Schicht 2 verwendet wird.

δ (2) = f ′ ( a (2) )=

$x$ ist ein Vektor von Eingabewerten.

Multipliziert man diese Vektoren miteinander, kann man alle partiellen Ableitungsterme in einem Ausdruck berechnen.

∂J( θ ) ∂ θ ij (1) ==

Wenn Sie es bis hierher geschafft haben, herzlichen Glückwunsch! Wir haben gerade alle partiellen Ableitungen berechnet, die notwendig sind, um den Gradientenabstieg anzuwenden und unsere Parameterwerte zu optimieren. Im nächsten Abschnitt werde ich Ihnen eine Möglichkeit vorstellen, den gerade entwickelten Prozess zu visualisieren und eine durchgängige Methode zur Implementierung der Backpropagation zu präsentieren.

Backpropagation

Im letzten Abschnitt haben wir einen Weg entwickelt, um alle für den Gradientenabstieg notwendigen partiellen Ableitungen (partielle Ableitung der Kostenfunktion nach allen Modellparametern) mit Hilfe von Matrixausdrücken zu berechnen. Bei der Berechnung der partiellen Ableitungen haben wir am Ende des Netzes begonnen und uns Schicht für Schicht bis zum Anfang zurückgearbeitet. Wir haben auch einen neuen Term $\delta$ entwickelt, der im Wesentlichen dazu dient, alle partiellen Ableitungs-Terme zu repräsentieren, die wir später wiederverwenden müssen, und wir arbeiten uns Schicht für Schicht rückwärts durch das Netz.

Hinweis: Backpropagation ist einfach eine Methode zur Berechnung der partiellen Ableitung der Kostenfunktion nach allen Parametern. Die eigentliche Optimierung der Parameter (Training) erfolgt durch Gradientenabstieg oder eine andere fortgeschrittene Optimierungstechnik.

Generell haben wir festgestellt, dass man die partiellen Ableitungen für die Schicht $l$ berechnen kann, indem man die $\delta$-Terme der nächsten Schicht vorwärts mit den Aktivierungen der aktuellen Schicht kombiniert.

$ \frac{{\partial J\left( \theta \right)}}{{\partial \theta _{ij}^{(l)}} = {\left( {{\delta ^{(l + 1)}} \rechts)^T}{a^{(l)}} $

Backpropagation visualisiert

Bevor ich das formale Verfahren der Backpropagation definiere, möchte ich eine Visualisierung des Prozesses geben.

Zunächst müssen wir die Ausgabe eines neuronalen Netzes mittels Vorwärtspropagation berechnen.

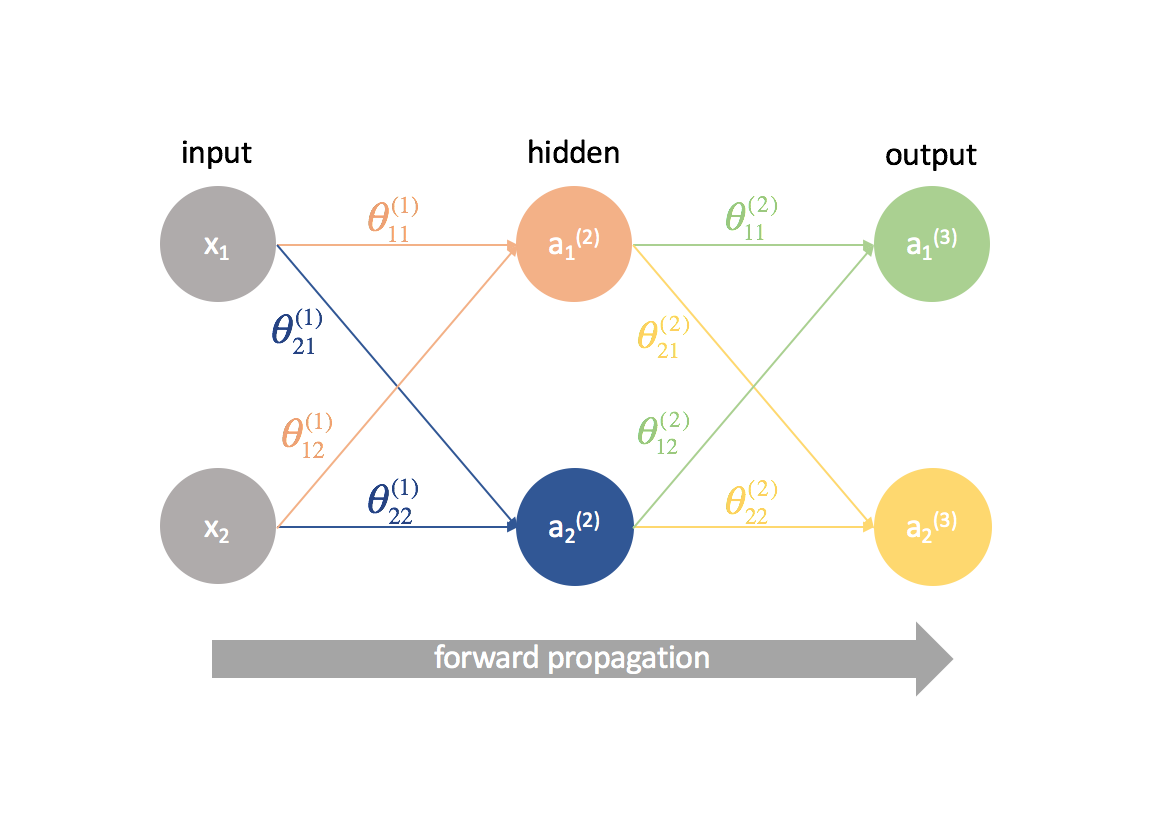
Nächstens berechnen wir die ${\delta ^{(3)}}$-Terme für die letzte Schicht im Netz. Denken Sie daran, dass diese $\delta$-Terme aus allen partiellen Ableitungen bestehen, die bei der Berechnung der Parameter für die weiter hinten liegenden Schichten wieder verwendet werden. In der Praxis bezeichnen wir $\delta$ typischerweise als den „Fehler“-Term.

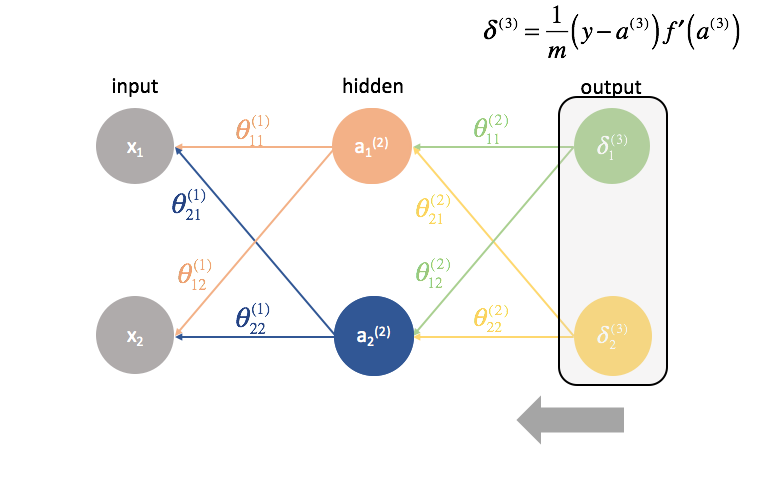
${\Theta ^{(2)}}$ ist die Matrix der Parameter, die Schicht 2 mit 3 verbindet. Wir multiplizieren den Fehler aus der dritten Schicht mit den Eingaben in der zweiten Schicht, um unsere partiellen Ableitungen für diesen Parametersatz zu berechnen.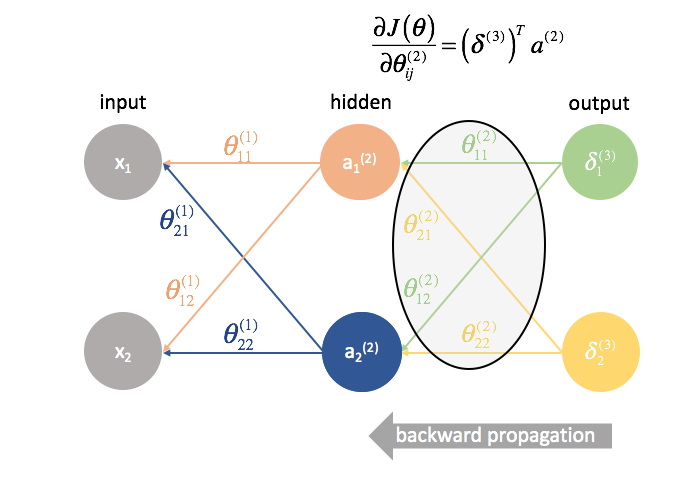

Als Nächstes „senden“ wir die „Fehler“-Terme auf genau dieselbe Weise zurück, wie wir die Eingaben an ein neuronales Netz „vorwärts senden“. Der einzige Unterschied ist, dass wir diesmal von hinten beginnen und einen Fehlerterm Schicht für Schicht rückwärts durch das Netzwerk schicken. Daher auch der Name: Backpropagation. Der Akt des „Zurückschickens unseres Fehlers“ wird über den Ausdruck ${\delta ^{(3)}}{\Theta ^{(2)}}$ bewerkstelligt.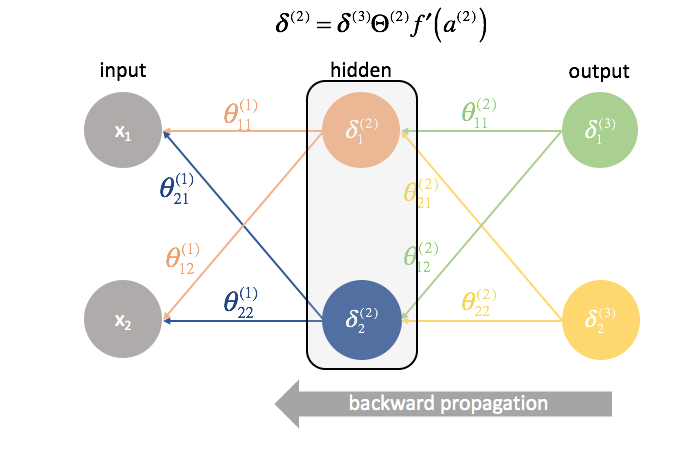

${\Theta ^{(1)}}$ ist die Matrix der Parameter, die Schicht 1 mit 2 verbindet. Wir multiplizieren den Fehler aus der zweiten Schicht mit den Eingaben in der ersten Schicht, um unsere partiellen Ableitungen für diesen Parametersatz zu berechnen.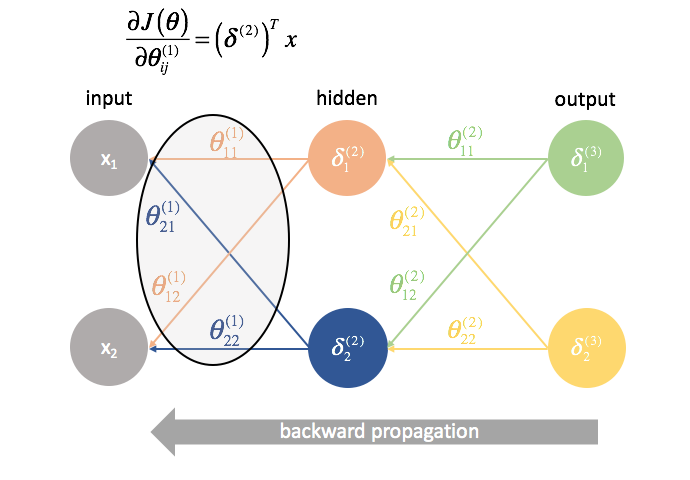

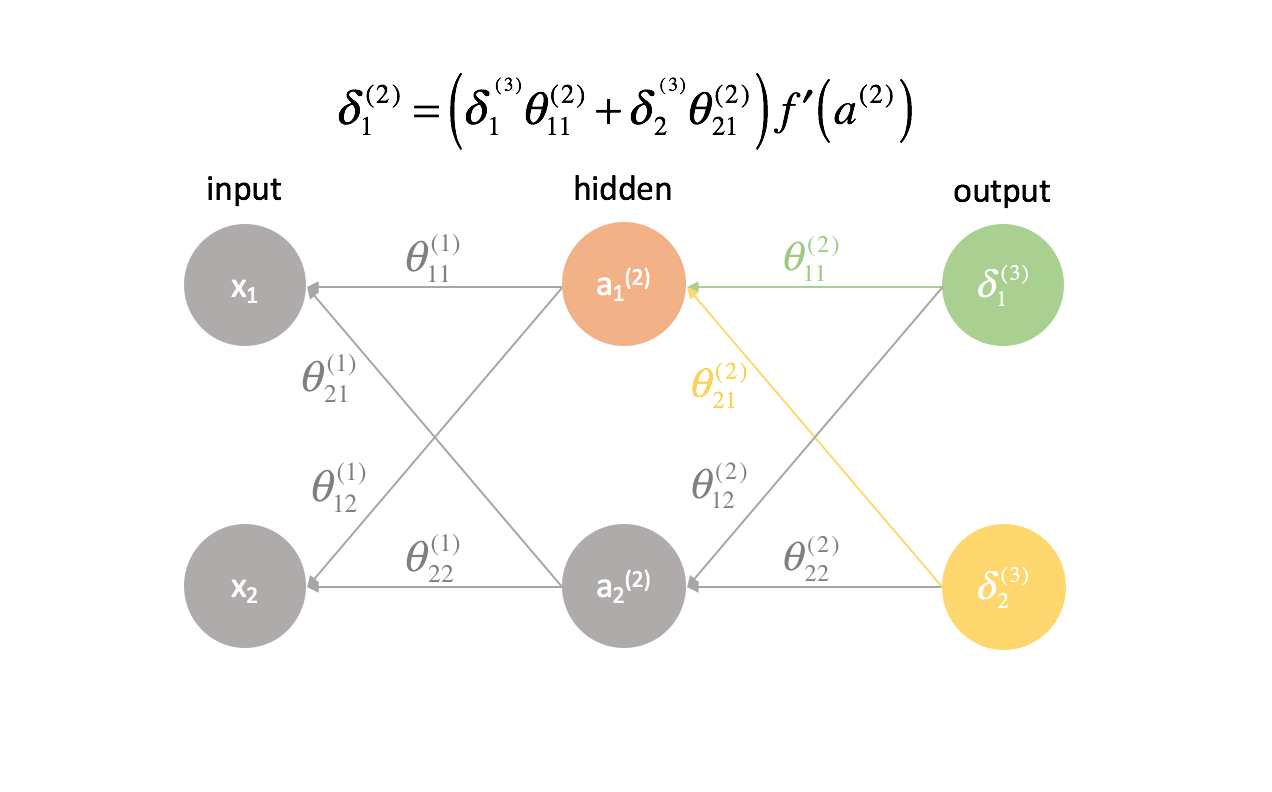
Für jede Schicht außer der letzten ist der „Fehler“-Term eine lineare Kombination von Parametern, die mit der nächsten Schicht verbunden sind (die sich vorwärts durch das Netzwerk bewegen) und den „Fehler“-Termen dieser nächsten Schicht. Dies gilt für alle versteckten Schichten, da wir keinen „Fehler“-Term für die Eingaben berechnen.

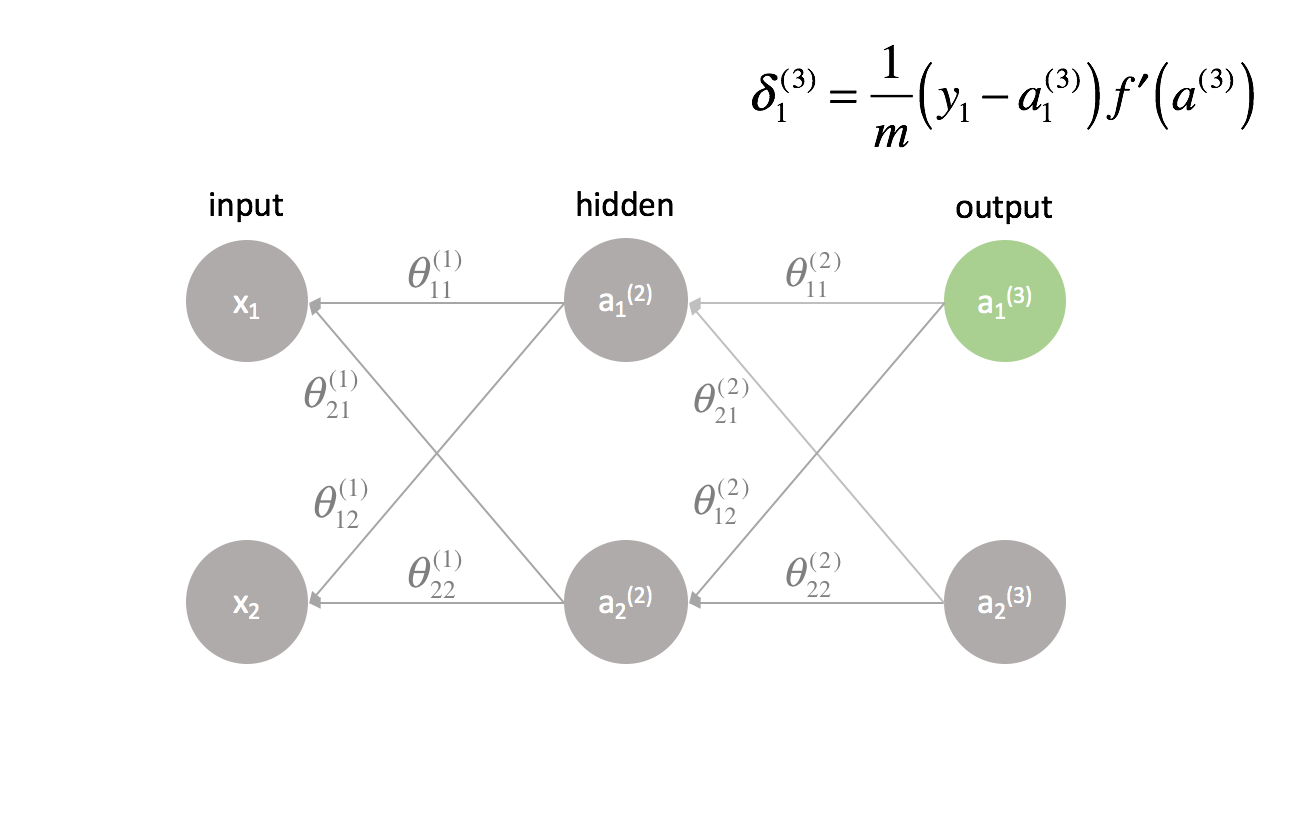
Die letzte Schicht ist ein Sonderfall, da wir die $\delta$-Werte berechnen, indem wir jedes Ausgangsneuron direkt mit seiner erwarteten Ausgabe vergleichen.

Ein formalisiertes Verfahren zur Implementierung der Backpropagation

Hier stelle ich ein praktisches Verfahren zur Implementierung der Backpropagation durch ein Netz von Schichten $l=1,2,…,L$.

1. Durchführen der Vorwärtspropagation.

2. Berechnen Sie den Term $\delta$ für die Ausgangsschicht.

3. Berechnen Sie die partiellen Ableitungen der Kostenfunktion bezüglich aller Parameter, die in die Ausgabeschicht eingehen, ${\Theta ^{(L – 1)}}$.

4. Gehen Sie eine Schicht zurück.
   $l = l – 1$

5. Berechnen Sie den Term $\delta$ für die aktuelle versteckte Schicht.

6. Berechnen Sie die partiellen Ableitungen der Kostenfunktion nach allen Parametern, die in die aktuelle Schicht einfließen.

7. Wiederholen Sie 4 bis 6, bis Sie die Eingabeschicht erreichen.

Wiederholung der Initialisierung der Gewichte

Als wir anfingen, schlug ich vor, dass wir unsere Gewichte einfach zufällig initialisieren, um einen Ausgangspunkt zu haben. So konnten wir die Vorwärtspropagation durchführen, die Ausgaben mit den erwarteten Werten vergleichen und die Kosten unseres Modells berechnen.

Es ist tatsächlich sehr wichtig, dass wir unsere Gewichte mit zufälligen Werten initialisieren, damit wir die Symmetrie in unserem Modell brechen können. Hätten wir alle unsere Gewichte gleich initialisiert, wäre jedes Neuron in der nächsten Schicht vorwärts gleich der gleichen Linearkombination von Werten.

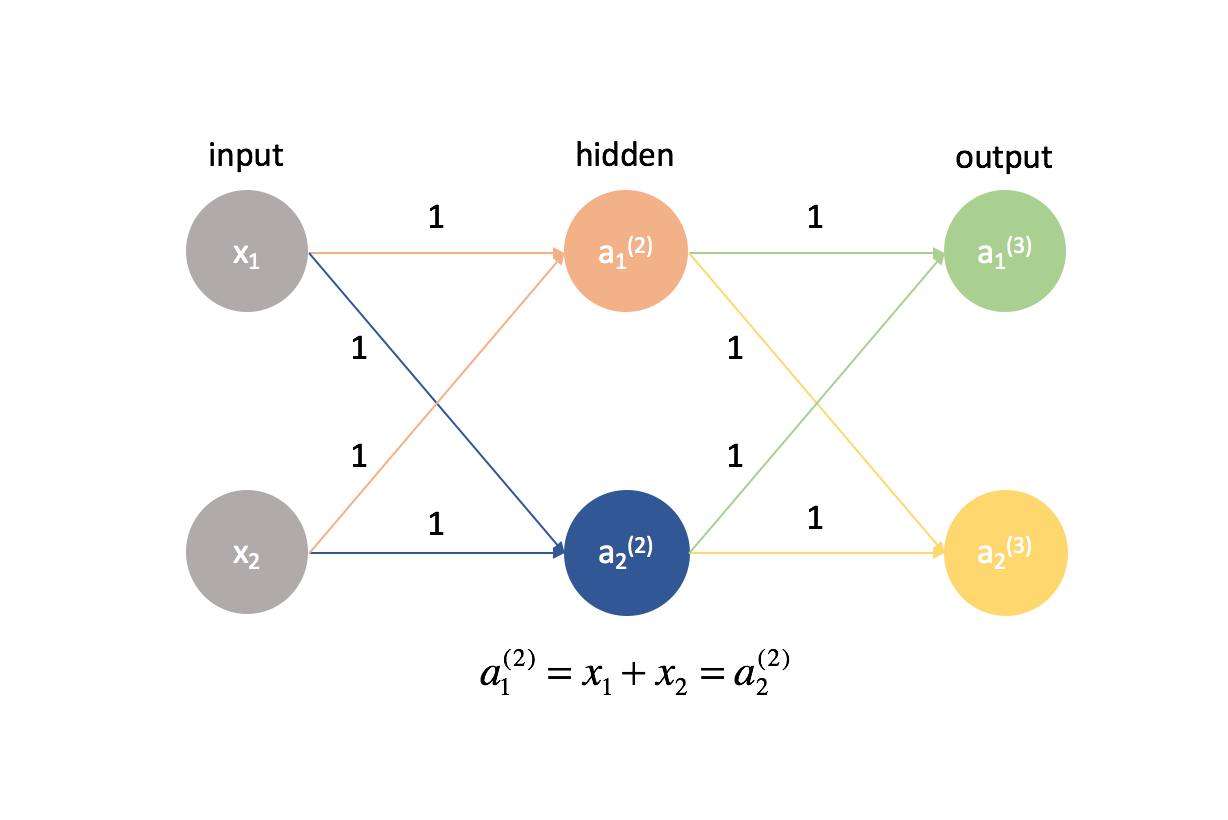
Nach der gleichen Logik wären auch die $\delta$-Werte für jedes Neuron in einer bestimmten Schicht gleich.

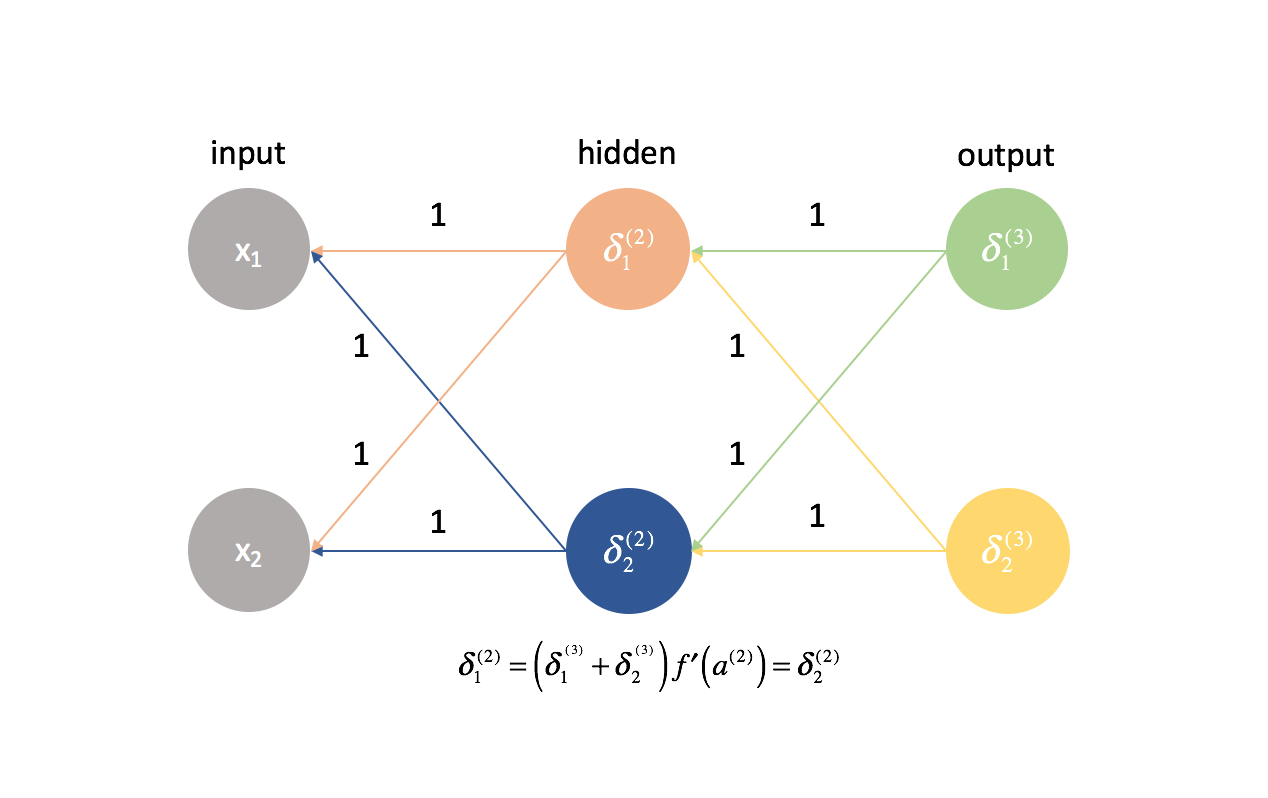
Da wir die partiellen Ableitungen in jeder gegebenen Schicht durch Kombination von $\delta$-Werten und Aktivierungen berechnen, wären alle partiellen Ableitungen in jeder gegebenen Schicht identisch. Somit würden sich die Gewichte beim Gradientenabstieg symmetrisch aktualisieren und mehrere Neuronen in einer Schicht wären nutzlos. Dies wäre offensichtlich kein sehr hilfreiches neuronales Netzwerk.

Die zufällige Initialisierung der Gewichte des Netzwerks ermöglicht es uns, diese Symmetrie zu brechen und jedes Gewicht individuell entsprechend seiner Beziehung zur Kostenfunktion zu aktualisieren. Typischerweise weisen wir jedem Parameter einen zufälligen Wert in $\left$ zu, wobei $\varepsilon$ ein Wert nahe Null ist.

Alles zusammenfügen

Nachdem wir alle partiellen Ableitungen für die Parameter des neuronalen Netzes berechnet haben, können wir den Gradientenabstieg zur Aktualisierung der Gewichte verwenden.

Im Allgemeinen haben wir den Gradientenabstieg wie folgt definiert

wobei $\Delta {\theta _i}$ der „Schritt“ ist, den wir entlang des Gradienten gehen, skaliert mit einer Lernrate, $\eta$.

Wir verwenden diese Formel, um jede der Gewichte zu aktualisieren, die Vorwärtspropagation mit den neuen Gewichten neu zu berechnen, den Fehler rückwärts zu propagieren und die nächste Aktualisierung der Gewichte zu berechnen. Dieser Prozess wird fortgesetzt, bis wir zu einem optimalen Wert für unsere Parameter konvergiert haben.

Während jeder Iteration führen wir Vorwärtspropagation durch, um die Ausgaben zu berechnen, und Rückwärtspropagation, um die Fehler zu berechnen; eine vollständige Iteration wird als Epoche bezeichnet. Es ist üblich, nach jeder Epoche Auswertungsmetriken auszugeben, damit wir die Entwicklung unseres neuronalen Netzwerks während des Trainings beobachten können.

Weitere Lektüre

• Die Matrixberechnung, die Sie für Deep Learning benötigen

• Wie der Backpropagation-Algorithmus funktioniert

• Stanford cs231n: Backpropagation, Intuitionen

• CS231n Winter 2016: Vorlesung 4: Backpropagation, Neuronale Netze 1

• Vorlesungen zu Deep Learning

• Ja, Backprop sollte man verstehen

• Bausteine neuronaler Netze

• Und falls Sie bei Backpropagation einfach aufgegeben haben… Deep Learning ohne Backpropagation