Darrell Henry, Louisiana State University
Nelson Eby, University of Massachusetts – Lowell
John Goodge, University of Minnesota – Duluth
David Mogk, Montana State University
Wenn ein Kristall mit Röntgenstrahlen einer festen Wellenlänge (ähnlich dem Abstand der atomaren Kristallgitterebenen) und unter bestimmten Einfallswinkeln beschossen wird, entstehen intensive reflektierte Röntgenstrahlen, wenn die Wellenlängen der gestreuten Röntgenstrahlen konstruktiv interferieren. Damit die Wellen konstruktiv interferieren, müssen die Unterschiede im Laufweg gleich ganzzahligen Vielfachen der Wellenlänge sein. Wenn diese konstruktive Interferenz auftritt, verlässt ein gebeugter Röntgenstrahl den Kristall in einem Winkel, der dem des einfallenden Strahls entspricht.
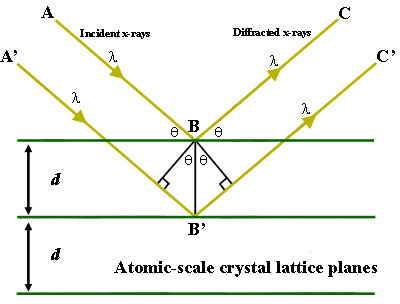
Abbildung 1. Reflexion nach dem Braggschen Gesetz. Die gebeugten Röntgenstrahlen zeigen eine konstruktive Interferenz, wenn sich der Abstand zwischen den Pfaden ABC und A’B’C‘ um eine ganzzahlige Anzahl von Wellenlängen (λ) unterscheidet.
Um diese Eigenschaft zu veranschaulichen, betrachte man einen Kristall mit Kristallgitter-Ebenenabständen d (rechts). Ist die Weglängendifferenz zwischen den Strahlengängen ABC und A’B’C‘ ein ganzzahliges Vielfaches der Wellenlänge, so tritt bei einer Kombination aus dieser spezifischen Wellenlänge, dem Kristallgitterebenenabstand und dem Einfallswinkel (Θ) konstruktive Interferenz auf. Jede rationale Ebene von Atomen in einem Kristall wird unter einem einzigen, einzigartigen Winkel gebrochen (für Röntgenstrahlen einer festen Wellenlänge).
Die allgemeine Beziehung zwischen der Wellenlänge der einfallenden Röntgenstrahlen, dem Einfallswinkel und dem Abstand zwischen den Kristallebenen der Atome ist als Braggsches Gesetz bekannt und wird wie folgt ausgedrückt:
n λ = 2d sinΘ
wobei n (eine ganze Zahl) die „Ordnung“ der Reflexion ist, λ die Wellenlänge der einfallenden Röntgenstrahlen ist, d der Abstand zwischen den Kristallebenen ist und Θ der Einfallswinkel ist.
Anwendungen des Braggschen Gesetzes.
- In der Röntgenbeugung (XRD) wird der Interplanarabstand (d-Abstand) eines Kristalls zur Identifikation und Charakterisierung verwendet. Dabei ist die Wellenlänge der einfallenden Röntgenstrahlung bekannt und es wird der Einfallswinkel (Θ) gemessen, bei dem konstruktive Interferenz auftritt. Die Lösung der Braggschen Gleichung liefert den d-Abstand zwischen den Kristallgitterebenen der Atome, die die konstruktive Interferenz erzeugen. Es ist zu erwarten, dass ein gegebener unbekannter Kristall viele rationale Ebenen von Atomen in seiner Struktur hat; daher kann die Sammlung der „Reflexionen“ aller Ebenen verwendet werden, um einen unbekannten Kristall eindeutig zu identifizieren. Im Allgemeinen neigen Kristalle mit hoher Symmetrie (z. B. isometrisches System) dazu, relativ wenige Atomebenen zu haben, während Kristalle mit niedriger Symmetrie (im triklinen oder monoklinen System) dazu neigen, eine große Anzahl möglicher Atomebenen in ihrer Struktur zu haben.
- Im Falle der wellenlängendispersiven Spektrometrie (WDS) oder der Röntgenfluoreszenzspektroskopie (XRF) werden Kristalle mit bekannten d-Abständen als Analysekristalle im Spektrometer verwendet. Da die Position der Probe und des Detektors bei diesen Anwendungen fest ist, wird die Winkelposition des reflektierenden Kristalls gemäß dem Braggschen Gesetz verändert, so dass eine bestimmte Wellenlänge von Interesse auf einen Detektor zur quantitativen Analyse gelenkt werden kann. Jedes Element im Periodensystem hat einen diskreten Energieunterschied zwischen den Orbital-„Schalen“ (z. B. K, L, M), so dass jedes Element Röntgenstrahlen einer festen Wellenlänge erzeugt. Daher ist es durch die Verwendung eines Spektrometerkristalls (mit festem d-Abstand des Kristalls) und die Positionierung des Kristalls in einem eindeutigen und festen Winkel (Θ) möglich, die interessierenden Elemente auf der Grundlage der charakteristischen Röntgenwellenlängen, die von jedem Element erzeugt werden, zu erkennen und zu quantifizieren.
Literatur
Eby, G.N., 2004, Principles of Environmental Geochemistry. Brooks/Cole-Thomson Learning, S. 212-214.