Heading

Just another blog

Distribuzione binomiale

MathWorld Contributors > Yap >

Scaricare Quaderno di MathematicaESPLORA QUESTO ARGOMENTO NELLA CLASSE DI MathWorldDistribuzione binomiale

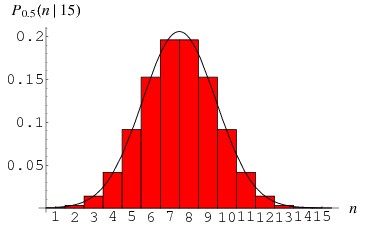
La distribuzione binomiale fornisce la distribuzione di probabilità discreta P_p(n|N) di ottenere esattamente n successi su N prove di Bernoulli (dove il risultato di ogni prova di Bernoulli è vero con probabilità p e falso con probabilità q=1-p). La distribuzione binomiale è quindi data da

P_p(n|N) = (N; n)p^nq^(N-n)
(1)
= (N!)/(n!(N-n)!)p^n(1-p)^(N-n),
(2)

dove (N; n) è un coefficiente binomiale. Il grafico sopra mostra la distribuzione di n successi su N=20 prove con p=q=1/2.

La distribuzione binomiale è implementata nel linguaggio Wolfram come BinomialDistribution.

La probabilità di ottenere più successi del n osservato in una distribuzione binomiale è

P=somma_(k=n+1)^N(N; k)p^k(1-p)^(N-k)=I_p(n+1,N-n),
(3)

dove

I_x(a,b)=(B(x;a,b))/(B(a,b)),
(4)

B(a,b) è la funzione beta, e B(x;a,b) è la funzione beta incompleta.

La funzione caratteristica della distribuzione binomiale è

phi(t)=(q+pe^(it))^N
(5)

(Papoulis 1984, p. 154). Il momento-generatrice di momenti M per la distribuzione è

M(t) = e^(tn)
(6)
= sum_(n=0)^(N)e^(tn)(N; n)p^nq^(N-n)
(7)
= sum_(n=0)^(N)(N; n)(pe^t)^n(1-p)^(N-n)
(8)
= ^N
(9)
M^'(t)'(t) = N^(N-1)(pe^t)
(10)
M^('')(t)'')(t) = N(N-1)^(N-2)(pe^t)^2+N^(N-1)(pe^t).
(11)

La media è

mu = M^'(0)'(0)
(12)
= N(p+1-p)p
(13)
= Np.
(14)

I momenti intorno a 0 sono

mu_1^'' = mu=Np
(15)
mu_2^'' = Np(1-p+Np)
(16)
mu_3^'' = Np(1-3p+3Np+2p^2-3Np^2+N^2p^2)
(17)
mu_4^'' = Np(1-7p+7Np+12p^2-18Np^2+6N^2p^2-6p^3+11Np^3-6N^2p^3+N^3p^3),
(18)

così i momenti sulla media sono

mu_2 = Np(1-p)=Npq
(19)
mu_3 = Np(1-p)(1-2p)
(20)
mu_4 = Np(1-p).
(21)

L’asimmetria e la curtosi sono

gamma_1 = (1-2p)/(sqrt(Np(1-p))
(22)
= (q-p)/(sqrt(Npq))
(23)
gamma_2 = (6p^2-6p+1)/(Np(1-p))
(24)
= (1-6pq)/(Npq).
(25)

La prima cumulante è

kappa_1=np,
(26)

e le cumulanti successive sono dati dalla relazione di ricorrenza

kappa_(r+1)=pq(dkappa_r)/(dp).
(27)

La deviazione media è data da

MD=sum_(k=0)^N|k-Np|(N; k)p^k(1-p)^(N-k).
(28)

Per il caso speciale p=q=1/2, questo è uguale a

MD = 2^(-N)sum_(k=0)^(N)(N; k)|k-1/2N|
(29)
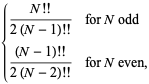= {(N!!)/(2(N-1)!!) per N dispari; ((N-1)!!)/(2(N-2)!) per N pari,
(30)

dove N!! è un fattoriale doppio. Per N=1, 2, …, i primi valori sono quindi 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, … (OEIS A086116 e A086117). Il caso generale è dato da

MD=2(1-p)^(N-|_Np_|)p^(|_Np_|+1)(|_Np_|+1)(N; |_Np_|+1).
(31)

Steinhaus (1999, pp. 25-28) considera il numero atteso di quadrati S(n,N,s) contenenti un dato numero di grani n su tavola di dimensioni s dopo una distribuzione casuale di N di grani,

S(n,N,s)=sP_(1/s)(n|N).
(32)

Prendendo N=s=64 si hanno i risultati riassunti nella seguente tabella.

n S(n,64,64)
0 23.3591
1 23.7299
2 11.8650
3 3.89221
4 0,942162
5 0.179459
6 0.0280109
7 0.0036840
8 4.16639×10^(-4)
9 4.11495×10^(-5)
10
3.59242×10^(-6)

Un’approssimazione alla distribuzione binomiale per grandi N può essere ottenuta espandendo intorno al valore n^~ dove P(n) è un massimo, i.e., dove dP/dn=0. Poiché la funzione logaritmo è monotona, possiamo invece scegliere di espandere il logaritmo. Sia n=n^~+eta, allora

ln=ln+B_1eta+1/2B_2eta^2+1/(3!)B_3eta^3+...,
(33)

dove

B_k=)/(dn^k)]_(n=n^~).
(34)

Ma stiamo espandendo sul massimo, quindi, per definizione,

B_1=)/(dn)]_(n=n^~)=0.
(35)

Questo significa anche che B_2 è negativo, quindi possiamo scrivere B_2=-|B_2|. Ora, prendendo il logaritmo di (◇) si ottiene

ln=lnN!-lnn!-ln(N-n)!+nlnp+(N-n)lnq.
(36)

Per grandi n e N-n possiamo usare l’approssimazione di Stirling

ln(n!) circa nlnn-n,
(37)

così

(d)/(dn) circa (lnn+1)-1
(38)
= lnn
(39)
(d)/(dn) circa d/(dn)
(40)
=
(41)
= -ln(N-n),
(42)

e

(dln)/(dn) circa -lnn+ln(N-n)+lnp-lnq.
(43)

Per trovare n^~, impostare questa espressione su 0 e risolvere per n,

ln((N-n^~)/(n^~)p/q)=0
(44)
(N-n^~)/(n^~)p/q=1
(45)
(N-n^~)p=n^~q
(46)
n^~(q+p)=n^~=Np,
(47)

siccome p+q=1. Possiamo ora trovare i termini dell’espansione

B_2 = )/(dn^2)]_(n=n^~)
(48)
= -1/(n^~)-1/(N-n^~)
(49)
= -1/(Npq)
(50)
= -1/(Np(1-p))
(51)
B_3 = )/(dn^3)]_(n=n^~)
(52)
= 1/(n^~^2)-1/((N-n^~)^2)
(53)
= (q^2-p^2)/(N^2p^2q^2)
(54)
= (1-2p)/(N^2p^2(1-p)^2)
(55)
B_4 = )/(dn^4)]_(n=n^~)
(56)
= -2/(n^~^3)-2/((n-n^~)^3)
(57)
= (2(p^2-pq+q^2))/(N^3p^3q^3)
(58)
= (2(3p^2-3p+1))/(N^3p^3(1-p)^3)).
(59)

BinomialGaussian

Ora, trattando la distribuzione come continua,

lim_(N-infty)sum_(n=0)^NP(n) approx intP(n)dn=int_(-infty)^inftyP(n^~+eta)deta=1.
(60)

Siccome ogni termine è di ordine 1/N∼1/sigma^2 minore del precedente, possiamo ignorare i termini superiori a B_2, quindi

P(n)=P(n^~)e^(-|B_2|eta^2/2).
(61)

La probabilità deve essere normalizzata, quindi

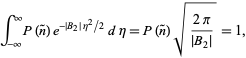int_(-infty)^inftyP(n^~)e^(-|B_2|eta^2/2)deta=P(n^~)sqrt((2pi)/(|B_2|))=1,
(62)

e

P(n) = sqrt((|B_2|)/(2pi))e^(-|B_2|(n-n^~)^2/2)
(63)
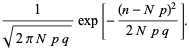= 1/(sqrt(2piNpq))exp.
(64)

Definendo sigma^2=Npq,

P(n)=1/(sigmasqrt(2pi))exp,
(65)

che è una distribuzione normale. La distribuzione binomiale è quindi approssimata da una distribuzione normale per qualsiasi p fisso (anche se p è piccolo) come N è portato a infinito.

Se N-infty e p-0 in modo tale che Np-lambda, allora la distribuzione binomiale converge alla distribuzione Poisson con media lambda.

Lasciamo che x e y siano variabili casuali binomiali indipendenti caratterizzate dai parametri n,p e m,p. La probabilità condizionata di x dato che x+y=k è

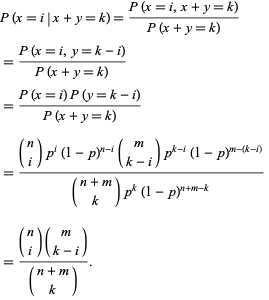P(x=i|x+y=k)=(P(x=i,x+y=k))/(P(x+y=k)) =(P(x=i,y=k-i))/(P(x+y=k)) =(P(x=i)P(y=k-i))/(P(x+y=k)) =((n; i)p^i(1-p)^(n-i)(m; k-i)p^(k-i)(1-p)^(m-(k-i)))/((n+m; k)p^k(1-p)^(n+m-k)) =((n; i)(m; k-i))/((n+m; k)).
(66)

Nota che questa è una distribuzione ipergeometrica.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *