Siguiente: 8.5 Ciclos de potencia de Rankine Subir: 8. Ciclos de potencia con Anterior: 8.3 El ciclo de Carnot Índice
Hasta ahora sólo hemos considerado los gases ideales y queremos demostrar que las propiedades ![]()
![]()
![]() , etc. son verdaderas variables de estado y que las leyes 1ª y 2ª de la termodinámica se cumplen cuando el medio de trabajo no es un gas ideal (es decir, un medio bifásico). Una forma elegante de hacerlo es considerar un ciclo de Carnot para un medio bifásico. Afirmar que todos los motores de Carnot que funcionan entre dos temperaturas determinadas tienen el mismo rendimiento es una forma de enunciar la2ª ley de la termodinámica. El fluido de trabajo no tiene por qué ser un gas ideal y puede ser un medio bifásico que cambia de fase.
, etc. son verdaderas variables de estado y que las leyes 1ª y 2ª de la termodinámica se cumplen cuando el medio de trabajo no es un gas ideal (es decir, un medio bifásico). Una forma elegante de hacerlo es considerar un ciclo de Carnot para un medio bifásico. Afirmar que todos los motores de Carnot que funcionan entre dos temperaturas determinadas tienen el mismo rendimiento es una forma de enunciar la2ª ley de la termodinámica. El fluido de trabajo no tiene por qué ser un gas ideal y puede ser un medio bifásico que cambia de fase.
La idea es hacer funcionar un motor de Carnot entre las temperaturas ![]() y
y![]() para un medio bifásico y dejar que sufra un cambio de fase. Entonces podemos derivar una relación importante conocida como la ecuación de Clausius-Clapeyron, que da la pendiente de la curva de presión de vapor. Podemos entonces medir la curva de presión de vapor de varias sustancias y comparar la pendiente medida con la ecuación de Clausius-Clapeyron. Esto puede considerarse como una prueba experimental de la validez general de la primera y segunda ley de la termodinámica.8:Ciclo de Carnot ideado para probar la validez de las leyes de la termodinámica
para un medio bifásico y dejar que sufra un cambio de fase. Entonces podemos derivar una relación importante conocida como la ecuación de Clausius-Clapeyron, que da la pendiente de la curva de presión de vapor. Podemos entonces medir la curva de presión de vapor de varias sustancias y comparar la pendiente medida con la ecuación de Clausius-Clapeyron. Esto puede considerarse como una prueba experimental de la validez general de la primera y segunda ley de la termodinámica.8:Ciclo de Carnot ideado para probar la validez de las leyes de la termodinámica
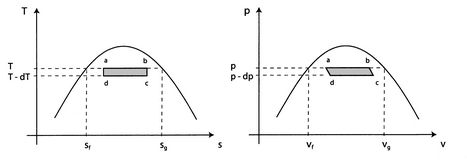
Considere el ciclo infinitesimal de Carnot ![]() mostrado en laFigura 8.8. El calor se absorbe entre los estados
mostrado en laFigura 8.8. El calor se absorbe entre los estados![]() y
y ![]() . Para vaporizar una cantidad arbitraria de masa,
. Para vaporizar una cantidad arbitraria de masa, ![]() , la cantidad de calor
, la cantidad de calor
| (8..1) |
debe ser suministrado al sistema. A partir de las leyes 1ª y 2ª de la termodinámica, el rendimiento térmico para un ciclo de Carnot puede escribirse como
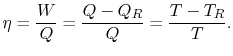 |
Por tanto, para el ciclo infinitesimal considerado anteriormente,
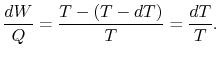 |
(8..2) |
El trabajo a lo largo de ![]() y
y ![]() casi se anulan de manera que el trabajo neto es la diferencia entre el trabajo a lo largo de
casi se anulan de manera que el trabajo neto es la diferencia entre el trabajo a lo largo de ![]() y
y ![]() , y
, y ![]() puede verse como el área encerrada por el rectángulo
puede verse como el área encerrada por el rectángulo ![]() :
:
| (8..3) |
Sustituyendo las ecuaciones (8.1) y(8.3) en (8.2) oneobtains
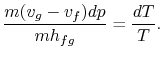 |
Al reordenar los términos se obtiene la ecuación de Clausius-Clapeyron,que define la pendiente de la curva de presión de vapor:
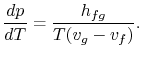 |
(8..4) |
La belleza es que hemos encontrado una relación general entre cantidades medibles experimentalmente a partir de primeros principios(1ª y 2ª leyes de la termodinámica).
Para trazar la relación Clausius-Clapeyron y compararla con las curvas de presión de vapor medidas experimentalmente, necesitamos integrar la ecuación (8.4). Para ello, el calor de vaporización y los volúmenes específicos deben ser funciones conocidas de la temperatura. Este es un problema importante en fisicoquímica, pero no lo trataremos aquí, excepto para mencionar que si
- se pueden despreciar las variaciones del calor de vaporización,
- se supone que la fase de vapor es un gas ideal y
- el volumen específico del líquido es pequeño comparado con el de la fase vapor,
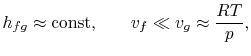 |
. |
la integración puede realizarse fácilmente8.1. Haciendo estas aproximaciones, la ecuación de Clausius-Clapeyronequation se convierte en
 |
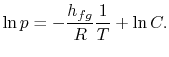 |
Nota que que las curvas de presión de vapor son líneas rectas si se traza ![]() frente a
frente a ![]() y que la pendiente de las curvas está
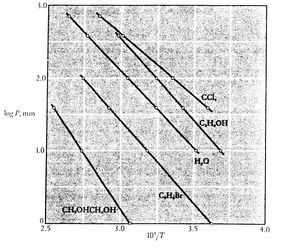
y que la pendiente de las curvas está![]() , directamente relacionada con el calor de vaporización.Las figuras 8.9, 8.9 y 8.22 muestran las curvas de presión de vapor para diversas sustancias. El hecho de que todas las sustancias conocidas en la región bifásica cumplan la ecuación de Clausius-Clapeyron demuestra la validez general de la primera y segunda leyes de la termodinámica.
, directamente relacionada con el calor de vaporización.Las figuras 8.9, 8.9 y 8.22 muestran las curvas de presión de vapor para diversas sustancias. El hecho de que todas las sustancias conocidas en la región bifásica cumplan la ecuación de Clausius-Clapeyron demuestra la validez general de la primera y segunda leyes de la termodinámica.

Siguiente: 8.5 Ciclos de potencia de Rankine Subir: 8. Ciclos de potencia con Anterior: 8.3 El ciclo de Carnot Índice de contenidos
UnifiedTP