Un algoritmo de dividir y conquistar es una estrategia de resolución de un problema grande mediante
- la división del problema en subproblemas más pequeños
- la resolución de los subproblemas, y
- la combinación de los mismos para obtener el resultado deseado.
Para utilizar el algoritmo de dividir y conquistar, se utiliza la recursión. Conoce la recursión en diferentes lenguajes de programación:
- Recursión en Java
- Recursión en Python
- Recursión en C++
¿Cómo funcionan los algoritmos de divide y vencerás?
Aquí tienes los pasos que se siguen:
- Divide: Dividir el problema dado en subproblemas utilizando la recursividad.
- Conquistar: Resolver los subproblemas más pequeños recursivamente. Si el subproblema es lo suficientemente pequeño, entonces resolverlo directamente.
- Combinar: Combinar las soluciones de los subproblemas que forman parte del proceso recursivo para resolver el problema real.
- Dejemos que el array dado sea:

Array para la ordenación por fusión - Dividamos el array en dos mitades.

Divide el array en dos subpartidas Vuelve a dividir cada subpartida recursivamente en dos mitades hasta obtener elementos individuales.
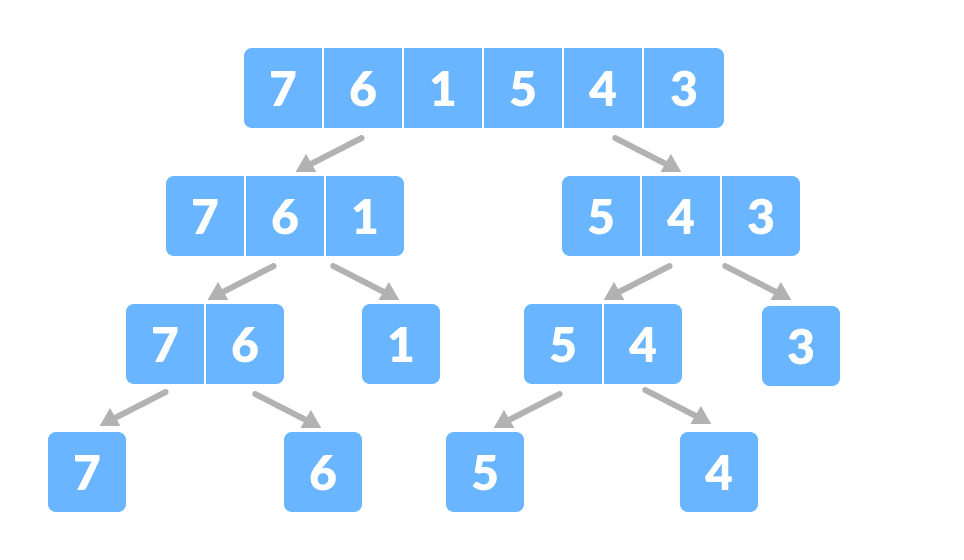
Divide el array en subpartes más pequeñas - Ahora, combina los elementos individuales de forma ordenada. Aquí, los pasos de conquistar y combinar van de la mano.
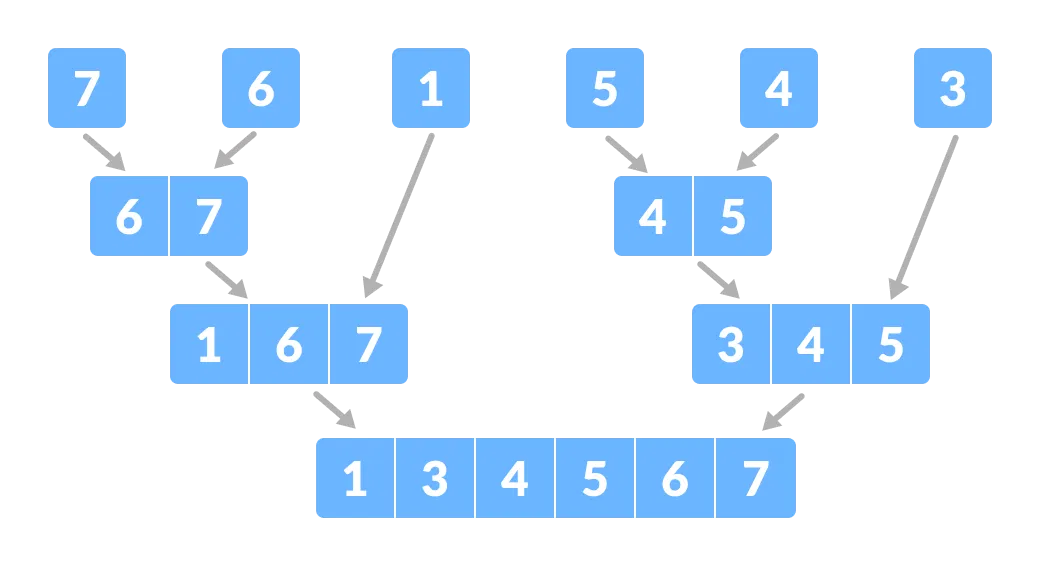
Combinar los subpartes .
- La complejidad para la multiplicación de dos matrices utilizando el método ingenuo es O(n3), mientras que utilizando el enfoque de dividir y conquistar (es decir, la multiplicación matricial de Strassen) es O(n2,8074). Este enfoque también simplifica otros problemas, como la Torre de Hanoi.
- Este enfoque es adecuado para sistemas multiprocesadores.
- Hace un uso eficiente de las cachés de memoria.
- Búsqueda binaria
- Ordenación por fusión
- Ordenación rápida
- Multiplicación de matrices de Strassen
- Algoritmo de Karatsuba
Entendamos este concepto con la ayuda de un ejemplo.
Aquí, vamos a ordenar un array utilizando el enfoque de divide y vencerás (es decir. ordenación por fusión).
Complejidad temporal
La complejidad del algoritmo divide y vencerás se calcula utilizando el teorema maestro.
T(n) = aT(n/b) + f(n),where,n = size of inputa = number of subproblems in the recursionn/b = size of each subproblem. All subproblems are assumed to have the same size.f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions
Tomemos un ejemplo para encontrar la complejidad temporal de un problema recursivo.
Para una ordenación por fusión, la ecuación se puede escribir como:
T(n) = aT(n/b) + f(n) = 2T(n/2) + O(n)Where, a = 2 (each time, a problem is divided into 2 subproblems)n/b = n/2 (size of each sub problem is half of the input)f(n) = time taken to divide the problem and merging the subproblemsT(n/2) = O(n log n) (To understand this, please refer to the master theorem.)Now, T(n) = 2T(n log n) + O(n) ≈ O(n log n)
Divide y vencerás vs enfoque dinámico
Utilice el enfoque de dividir y conquistar cuando el mismo subproblema no se resuelva varias veces. Utilice el enfoque dinámico cuando el resultado de un subproblema se vaya a utilizar varias veces en el futuro.
Entendamos esto con un ejemplo. Supongamos que intentamos encontrar la serie de Fibonacci. Entonces,
Enfoque de dividir y conquistar:
fib(n) If n < 2, return 1 Else , return f(n - 1) + f(n -2)
Enfoque dinámico:
mem = fib(n) If n in mem: return mem else, If n < 2, f = 1 else , f = f(n - 1) + f(n -2) mem = f return f
En un enfoque dinámico, mem almacena el resultado de cada subproblema.
Ventajas del Algoritmo de Dividir y Conquistar
Aplicaciones de divide y vencerás
.



