Construir escaleras para su terraza, patio o jardín es una tarea increíblemente difícil.
Antes de colocar sus herramientas y comenzar, necesita asegurarse de que cada escalón será idéntico tanto en tamaño como en forma.
Para ello, hay muchos parámetros y medidas que debe tener en cuenta en sus cálculos.
Le mostraremos cómo se puede hacer esto fácilmente.
Nuestra calculadora de escaleras online puede ayudarle a hacer esta tarea en un abrir y cerrar de ojos.
¡Simplemente ponga los valores para el recorrido y la subida total, junto con algunas medidas para los peldaños individuales para calcular la disposición de su escalera!
Contenido:
Cómo calcular escaleras
Para utilizar nuestra calculadora de escaleras, necesitas introducir las siguientes medidas como mínimo:
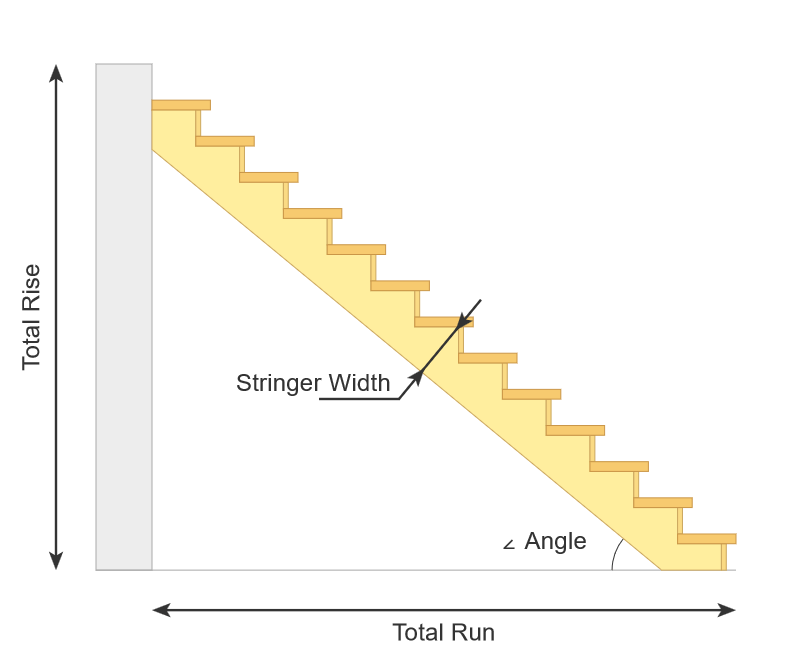
- Recorrido total – La longitud horizontal total del larguero de la escalera
- Subida total – La altura vertical entre la parte inferior del primer escalón y la parte superior del último escalón del larguero de la escalera
- .
- Ancho del larguero – La medida diagonal total entre el borde del peldaño y la línea de fondo
- Número de peldaños necesarios
- Para nuestros dos ejemplos de abajo, imaginamos que queremos tener 17 peldaños que suban hasta un rellano con una altura vertical total de 120 pulgadas y un recorrido horizontal total de 180 pulgadas
- Digamos que tenemos un grosor de banda de rodadura de 2 pulgadas
- Superposición de banda de rodadura de 2 pulgadas
- Espesor de peldaño de 1 pulgada
- Y una anchura de larguero de 12 pulgadas
- ¿Qué directrices o normativas debo tener en cuenta cuando planeo construir unas escaleras?
- ¿Qué propiedades deben cumplir con las normativas de construcción de mi país de origen para escaleras y escalones?
- ¿Qué pasa si las medidas de mis escaleras están en otras unidades métricas o imperiales?
- ¿Las escaleras de mi casa tienen que cumplir con las normas locales vigentes?
- ¿Hay alguna orientación o consejo sobre la longitud que deben tener mis escaleras?
- ¿Dónde puedo encontrar más información sobre las normas de escaleras para propiedades comerciales?
Utilizando estos valores, nuestra calculadora calcula la subida de altura vertical de cada escalón individual con la fracción:
$Subida = {Total\, Subida\Nsobre Número,de,Peldaños}$
Además, nuestra calculadora le permite elegir entre un montaje estándar y uno empotrado.
La decisión de utilizar un montaje sobre el otro dependerá de su situación individual y de su proyecto de bricolaje.

Avanzando en el artículo y en la explicación estas fórmulas son bastante abstractas y complicadas.
Para ayudar a seguirnos, haremos un ejemplo trabajado.
Esto pretende que los cálculos, fórmulas y explicaciones sean más fáciles de seguir.
Ejemplo de cálculos
Le llevaremos a través de los cálculos de ejemplo para primero un montaje estándar, y luego un conjunto de escaleras de montaje empotrado.
Al hacerlo, calcularemos las dimensiones de los peldaños y de la escalera.
Además, le mostraremos cómo la calculadora de largueros de escalera calcula la subida, el recorrido, el ángulo y la longitud de los largueros, permitiéndole planificar el diseño de su escalera prevista de forma eficaz.
Siga estos cálculos o simplemente utilice la calculadora para que su proyecto de bricolaje sea un éxito.
¿Suena bien? 😀
Cálculos del montaje estándar

Primero, calculamos la subida de altura vertical de cada escalón:
$Rise = {Total\,Rise \\Nsobre Number\,of,Steps} = {120\,in \Nsobre 17} = 7.06,in$
Ahora, utilizando una escalera de montaje estándar, la subida de altura vertical de los peldaños será un peldaño menos que con un montaje empotrado porque el último peldaño lo ocupa el entarimado. Por lo tanto, calculamos:
$Subida\Nde,los,peldaños = Total\NSubida – Subida = 120\N- 7,06\N- = 112,94\N$
Ahora, si incluimos el grosor de la huella (el grosor de la huella en cada peldaño), debemos restarlo también. La calculadora de escaleras de cubierta calcula así:
$Corrido,de,peldaños = Total,Recorrido – (Banda de rodadura,Solapamiento + Espesor de la huella) = 180,in – (2,in + 1,in) = 177,in$
Así, nuestra calculadora de escaleras de cubierta puede calcular la distancia horizontal total entre el borde de cada peldaño (¡sin olvidar que el último peldaño es la tarima!):
$Run = {Run\ de,pasos \ sobre Number\ de,pasos} = {177\ de,en \ sobre 16} = 11.06,in$
Ahora, si consideramos un solo peldaño de la escalera, la distancia horizontal total vendrá dada por:
$Total,Horizontal,= Recorrido + Peldaño,Solapamiento + Peldaño,Espesor = 11,06,in + 2,in + 1,in = 14,06,in$
Y el ángulo (¡o inclinación!) entre la horizontal y la escalera se calcula mediante:
$tan,\Nalpha_1 = {Subida,de,pasos \Nsobre Corrida,de,pasos} → \Nalpha_1 = tan^{-1} {Subida,de,pasos \Nsobre Corrida,de,pasos} = tan^{-1} {112.94\,in \over 177\,in} = 32,54^o$
Ahora, para hallar la longitud del larguero de la escalera se requiere algo de Matemáticas más complicadas. 🧐
¡Sigue el ejemplo de abajo para verlo en detalle!
Si consideramos el larguero, el ángulo entre el peldaño de la izquierda y la horizontal (α2) viene dado por la resta del ángulo calculado anteriormente a 90 grados:

$alpha_2 = 90^o – \alpha_1 = 90^o – 32,54^o = 57.46^o$
De forma similar,
$alpha_3 = 90^o + \alpha_2 = 90^o + 57.46^o = 147.46^o$
Y
$alpha_4 = \alpha_1 = 32.54^o$
$alpha_5 = 90^o + \alpha_1 = 90^o + 32.54^o = 122,54^o$
Además, la calculadora es capaz de averiguar las dimensiones horizontales y verticales del larguero.
Para facilitar la comprensión, de nuevo, vea la imagen de referencia. La calculadora calcula todas estas distancias utilizando el método que se indica a continuación:

$A_1 = Rise × sin\,\_2 = 7.06\\Nde pulgada × sin\N57,46^o = 5,95\Nde pulgada$
$A_2 = Anchura del larguero – A_1 = 12\Nde pulgada – 5,95\Nde pulgada = 6,05\Nde pulgada$
$C_2 = \Nsqrt{Run^2 – {A_1}^2} = \Nsqrt{(11.06,in)^2 – (5.95\,in)^2} = 9.32\$,in$
$C_3 = A_1 × tan\,|alpha_2 = 5.95\$,in × tan\$,57.46^o = 9.33\$
$B_1 = \$sqrt{Rise^2 – {A_1}^2} = \$sqrt{(7.06\,in)^2- (5.95\,in)^2} = 3.8\$,in$
$B_2 = A_2 × tan\,\Nalpha_1 = 6.05\\\Nen × tan\N32.54^o = 3.86\,in$
$B_3 = (Rise -Tread\,Thickness) × cos\,\alpha_2 = (7.06\,in – 2\,in) × cos\,57.46^o = 2.72\,in$
$A_3 = (Subida – Espesor de la banda de rodadura) × cos\,\alpha_1 = (7,06\,in – 2\,in) × cos\,32,54^o = 4,26\,in$
$A_4 = Anchura de la banda de rodadura – A_3 = 12\,in – 4.27,in = 7,74,in$
$C_4 = A_4 × tan, \N alfa_2 = 7,74,in × tan, 57,46^o = 12.12\,in$
Por último, la calculadora combina los valores calculados anteriormente para averiguar la longitud total del larguero de los peldaños:
$Stringer\,Length = C_3 + B_3 + (Number\,of,Steps – 1) × (B_1 + C_2) = 9.33\,in + 2,72\,in + (16-1) × (3,8\,in + 9,32\,in) = 208,88\,in$
Cálculos del montaje empotrado

Calcular la subida, el recorrido, el ángulo y la longitud del larguero para un montaje empotrado es muy similar al montaje estándar.
Simplemente recordamos que el último peldaño nos lleva a la tarima.
Como antes, calculamos la subida en altura vertical:
$Subida = {Total,Subida\NsobreNúmero,de\NPasos} = {120\Nen\N17} = 7.06,in$
A diferencia de la medida del montaje estándar, donde restamos el último escalón de la subida, con un montaje empotrado tenemos que:
$Subida,of,steps = Total,Rise = 120,in$
Sin embargo, en el último escalón, no tendremos ninguna huella (¡porque el último escalón es la propia tarima!) Así, transformamos las fórmulas anteriores para obtener la distancia de subida vertical:
$Subida,de,peldaños = Total,Subida – Peldaño,Espesor = 120,in – 2,in = 118,in$
Como antes, al incluir el peldaño al considerar el recorrido de los peldaños da:
$Recorrido,de,peldaños = Total,Recorrido – (Solapamiento de la banda de rodadura + Espesor del peldaño) = 180,in – (2,in + 1,in) = 177,in$
Así, nuestra calculadora calcula la distancia horizontal total entre el borde de cada peldaño.
La diferencia aquí es que tenemos 17 peldaños, ya que el último peldaño está incluido en el montaje a ras!
$Run = {Run\ de,peldaños \ sobre Number\ de,peldaños} = {177\ de,in \ sobre 17} = 10.41,in$
Considerando un solo paso, la distancia horizontal total vendrá dada por:
$Total,Horizontal,= Carrera + Pisada,Solapamiento,+ Espesor,= 10.41,in + 2,in + 1,in = 13.41,in$
Y el ángulo entre la horizontal y la escalera viene dado de nuevo por:
$tan,\Nalpha_1 = {Subida,de,pasos \Nsobre Corrida,de,pasos} → \Nalpha_1 = tan^{-1} {Subida,de,pasos \Nsobre Corrida,de,pasos} = tan^{-1} {120,in \Nsobre 177,in} = 34.14^o$
El cálculo de la longitud del larguero es el mismo método que para el montaje estándar.
La calculadora primero calcula los ángulos:

$alpha_2 = 90^o – \alpha_1 = 90^o – 34,14^o = 55,86^o$
$alpha_3 = 90^o + \alpha_2 = 90^o + 55.86^o = 145.86^o$
$alpha_4 = \alpha_1 = 34.14^o$
$alpha_5 = 90^o + \alpha_1 = 90^o + 34.14^o = 124.14^o$
Y la calculadora calcula el espaciado de las longitudes como antes:

$A_1 = Rise × sin\\,\alpha_2 = 7.06\\Nin × sin\N55,86^o = 5,84\Nin$
$A_2 = Anchura del larguero – A_1 = 12\Nin – 5,84\Nin = 6,16\Nin$
$C_2 = \Nsqrt{Run^2 – {A_1}^2} = \Nsqrt{(10.41\,in)^2 – (5,84\,in)^2} = 8,62\$,in$
$C_3 = A_1 × tan\,|alpha_2 = 5,84\,in × tan\,55,86^o = 8.62\,in$
$B_1 = \sqrt{Rise^2 – {A_1}^2} = \sqrt{(7.06\,in)^2- (5.84\,in)^2} = 3.96\$,in$
$B_2 = A_2 × tan\,\alpha_1 = 6.16\,in × tan\,34,14^o = 4,17\,in$
$B_3 = (Rise -Tread\,Thickness) × cos\,\alpha_2 = (7,06\,in – 2\,in) × cos\,55.86^o = 2.84\,in$
$A_3 = (Subida – Espesor de la banda de rodadura) × cos\,\alpha_1 = (7.06\,in – 2\,in) × cos\,34.14^o = 4.19\\$,in$
$A_4 = Anchura de la banda de rodadura,- A_3 = 12\$,in – 4.19\$,in = 7.81\$
$C_4 = A_4 × tan\$,\$2 = 7.Finalmente, la calculadora calcula la longitud total del larguero como antes:
$Longitud del larguero = C_3 + B_3 + (Número de pasos – 1) × (B_1 + C_2) = 8.62,in + 2,84\,in + (17-1) × (3,96\,in + 8,62\,in) = 212,72\,in$
¡Cuidado! ⚠️
Asegúrate de no redondear tu respuesta antes del cálculo final. ¡Estos pequeños errores de redondeo pueden tener una gran diferencia en la respuesta final!
¡Entendemos que esto es bastante difícil de seguir! Tenga la seguridad de que si no lo entiende, no se preocupe.
La calculadora lo hace todo por usted, trasladando el énfasis y la preocupación de usted a la tecnología. 😉
Preguntas frecuentes
Le recomendamos que conozca todas las normativas de construcción de su país de origen.
Nuestra calculadora está programada para dar medidas precisas dentro de las directrices del Council of American Building Officials y del International Code Council.
Debe consultar la normativa de construcción de su país de origen para obtener una respuesta exacta.
Sin embargo, una buena guía es que cualquier negocio o iglesia, organización, oficina o propiedad comercial debe cumplir con las normas de escaleras dadas de su país de origen.¡
Tenga cuidado – se expone a posibles multas sustanciales si no cumple con las normas de escaleras.
Use nuestra calculadora, investigue un poco y siga los ejemplos anteriores para asegurarse de que las cumple antes de empezar!
¡La respuesta es muy sencilla! Nuestra calculadora puede trabajar en muchas unidades diferentes al mismo tiempo.
La calculadora hace las conversiones por usted utilizando las siguientes relaciones:
$1\$,pie = 12\$,pulgadas = 0.33\,yardas = 30,48\,centímetros = 0,3048\,metros$
¡Así de fácil! 🙂
¡No! Como regla general, las normas de regulación de las escaleras de los edificios son aplicables para las propiedades comerciales que utilizan escaleras permanentes, no para las típicas escaleras domésticas, temporales o portátiles de uso personal.
Una buena orientación la da el Council of American Building Officials y el International Code Council.
Estas normativas recomiendan que la subida de la escalera no sea superior a 7,75 pulgadas (17,78 cm) y que el recorrido de la escalera no sea inferior a 10 pulgadas (25.4 cm).
Sin embargo, no olvide que esto es para una propiedad comercial.
Esto puede no ser práctico o necesario para su hogar, donde sus escaleras no tienen que cumplir con las mismas normas comerciales, pero deben ser utilizadas como una guía.
Hay mucha información que se puede encontrar en línea.
Recomendaríamos este sitio web como un gran punto de partida: https://codes.iccsafe.org/content/IBC2018P4/chapter-10-means-of-egress#IBC2018P4_Ch10_Sec1011. La sección 1011 tiene mucha información del código internacional de construcción 2018.