![]()
![]()

La distribución binomial da la distribución de probabilidad discreta ![]() de obtener exactamente
de obtener exactamente ![]() aciertos de
aciertos de ![]() ensayos Bernoulli (donde el resultado de cada ensayo Bernoulli es verdadero con probabilidad
ensayos Bernoulli (donde el resultado de cada ensayo Bernoulli es verdadero con probabilidad ![]() y falso con probabilidad
y falso con probabilidad ![]() ). La distribución binomial viene dada, por tanto, por
). La distribución binomial viene dada, por tanto, por
|
(1)
|
|||
|
(2)
|
donde ![]() es un coeficiente binomial. El gráfico anterior muestra la distribución de
es un coeficiente binomial. El gráfico anterior muestra la distribución de ![]() aciertos de
aciertos de ![]() ensayos con
ensayos con ![]() .
.
La distribución binomial se implementa en Wolfram Language como BinomialDistribution.
La probabilidad de obtener más aciertos que los ![]() observados en una distribución binomial es
observados en una distribución binomial es
|
(3)
|
donde
|
(4)
|
![]() es la función beta, y
es la función beta, y ![]() es la función beta incompleta.
es la función beta incompleta.
La función característica de la distribución binomial es
|
(5)
|
(Papoulis 1984, p. 154). El momentofunción generadora de momentos ![]() para la distribución es
para la distribución es
|
(6)
|
|||
|
(7)
|
|||
|
(8)
|
|||
|
(9)
|
|||
|
(10)
|
|||
|
(11)
|
La media es
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
Los momentos alrededor de 0 son
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
|||
|
(18)
|
Así que los momentos sobre la media son
|
(19)
|
|||
|
(20)
|
|||
|
(21)
|
La asimetría y la curtosidad son
|
(22)
|
|||
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
El primer cumulante es
|
(26)
|
y los cumulantes posteriores están dadas por la relación de recurrencia
|
(27)
|
La desviación media viene dada por
|
(28)
|
Para el caso especial ![]() , esto es igual a
, esto es igual a
|
(29)
|
|||
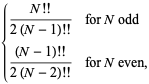 |
(30)
|
donde ![]() es un factorial doble. Para
es un factorial doble. Para ![]() , 2, …, los primeros valores son por tanto 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, … (OEIS A086116 y A086117). El caso general viene dado por
, 2, …, los primeros valores son por tanto 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, … (OEIS A086116 y A086117). El caso general viene dado por
|
(31)
|
Steinhaus (1999, pp. 25-28) considera el número esperado de cuadrados ![]() que contienen un número dado de granos
que contienen un número dado de granos ![]() en un tablero de tamaño
en un tablero de tamaño ![]() tras una distribución aleatoria de
tras una distribución aleatoria de ![]() de granos,
de granos,
|
(32)
|
Tomando ![]() se obtienen los resultados resumidos en la siguiente tabla.
se obtienen los resultados resumidos en la siguiente tabla.
| 0 | 23.3591 |
| 1 | 23,7299 |
| 2 | 11,8650 |
| 3 | 3.89221 |
| 4 | 0,942162 |
| 5 | 0.179459 |
| 6 | 0,0280109 |
| 7 | 0.0036840 |
| 8 | |
| 9 | |
| 10 | |
Una aproximación a la distribución binomial para grandes ![]() puede obtenerse expandiendo sobre el valor
puede obtenerse expandiendo sobre el valor ![]() donde
donde ![]() es un máximo, i.e., donde
es un máximo, i.e., donde ![]() . Como la función logaritmo es monótona, podemos optar por expandir el logaritmo. Sea
. Como la función logaritmo es monótona, podemos optar por expandir el logaritmo. Sea ![]() , entonces
, entonces
|
(33)
|
donde
|
(34)
|
Pero estamos expandiendo sobre el máximo, así que, por definición,
|
(35)
|
Esto también significa que ![]() es negativo, así que podemos escribir
es negativo, así que podemos escribir ![]() . Ahora, tomando el logaritmo de (◇) se obtiene
. Ahora, tomando el logaritmo de (◇) se obtiene
|
(36)
|
Para grandes ![]() y
y ![]() podemos utilizar la aproximación de Stirling
podemos utilizar la aproximación de Stirling
|
(37)
|
así que
|
(38)
|
|||
|
(39)
|
|||
|
(40)
|
|||
|
(41)
|
|||
|
(42)
|
y
|
(43)
|
Para encontrar ![]() , pon esta expresión a 0 y resuelve para
, pon esta expresión a 0 y resuelve para ![]() ,
,
|
(44)
|
|
(45)
|
|
(46)
|
|
(47)
|
ya que ![]() . Ahora podemos encontrar los términos de la expansión
. Ahora podemos encontrar los términos de la expansión
|
(48)
|
|||
|
(49)
|
|||
|
(50)
|
|||
|
(51)
|
|||
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
|||
|
(55)
|
|||
|
(56)
|
|||
|
(57)
|
|||
|
(58)
|
|||
|
(59)
|

Ahora, tratando la distribución como continua,
|
(60)
|
Dado que cada término es de orden ![]() menor que el anterior, podemos ignorar los términos superiores a
menor que el anterior, podemos ignorar los términos superiores a ![]() , por lo que
, por lo que
|
(61)
|
La probabilidad debe ser normalizada, así que
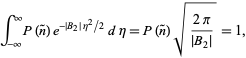 |
(62)
|
y
|
(63)
|
|||
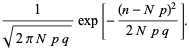 |
(64)
|
Definiendo ![]() ,
,
|
(65)
|
que es una distribución normal. Por tanto, la distribución binomial se aproxima por una distribución normal para cualquier ![]() fija (incluso si
fija (incluso si ![]() es pequeña) ya que
es pequeña) ya que ![]() se lleva a infinito.
se lleva a infinito.
Si ![]() y
y ![]() de forma que
de forma que ![]() , entonces la distribución binomial converge a la distribución de Poisson con media
, entonces la distribución binomial converge a la distribución de Poisson con media ![]() .
.
Sea ![]() y
y ![]() variables aleatorias binomiales independientes caracterizadas por los parámetros
variables aleatorias binomiales independientes caracterizadas por los parámetros ![]() y
y ![]() . La probabilidad condicional de
. La probabilidad condicional de ![]() dado que
dado que ![]() es
es
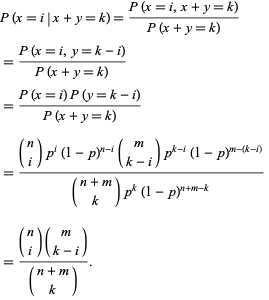 |
(66)
|
Nótese que se trata de una distribución hipergeométrica.