Vuelve al índice de lecciones | Haz las lecciones en orden | Página para imprimir
Factoriales
![]()
Los factoriales son cosas muy sencillas. Son sólo productos, indicados con un signo de exclamación. Por ejemplo, «cuatro factorial» se escribe como «¡4!» y significa 1×2×3×4 = 24. ¡En general, n! («enn factorial») significa el producto de todos los números enteros del 1 al n; es decir, n! = 1×2×3×…×n.
(Por diversas razones, 0! se define igual a 1, no a 0. Memoriza esto ahora: 0! = 1.)
- Evalúa 6!.
- ¡Simplifica 12! Copyright © Elizabeth Stapel 2004-2011 Todos los derechos reservados
- Simplifica lo siguiente:
- Simplifica lo siguiente:
- Simplifica lo siguiente:
1×2×3×4×5×6 = 720
Muchas (¿la mayoría?) calculadoras pueden evaluar factoriales por ti. Por ejemplo, el comando factorial está disponible en el menú «probabilidad» de una de mis calculadoras:
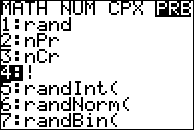

Busca un botón » ! «, o consulta el manual de instrucciones.
¡12! = 1×2×3×4×… Oh, al diablo con esto. ¿Dónde está mi calculadora…?

12! = 479001600
Advertencia
Cuando empieces a hacer combinaciones, permutaciones y probabilidad, estarás simplificando expresiones que tienen factoriales en los numeradores y en los denominadores. Por ejemplo:
![]()
Puedo hacer esto en mi calculadora:

También puedo trabajar a partir de la definición de un factorial:
![]()
En cualquier caso, 6! ÷ 4! = 30
Nota cómo he podido cancelar un montón de números en el problema anterior. Esto se debe a cómo se definen los factoriales, y esta propiedad puede simplificar mucho tu trabajo.
![]()
Ahora mismo puedo cancelar los factores del 1 al 14 que serán comunes a 17! y 14!. Entonces puedo simplificar lo que queda para obtener:
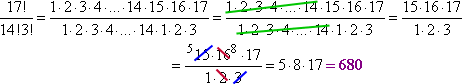
Nota cómo he acortado lo que tenía que escribir dejando un hueco (la «elipsis», o triple punto) en medio. Este proceso de dejar un hueco y cancelar será muy útil más adelante (como en el cálculo, donde usarás mucho esta técnica), sobre todo cuando te enfrentes a expresiones que tu calculadora no pueda manejar. Por ejemplo:
![]()
Mi calculadora no puede evaluar esto por mí, ya que estoy tratando con variables en lugar de números. Tendré que simplificar esto a mano. Para ello, escribiré los factoriales, usando suficientes factores para tener cosas que se puedan cancelar. Volviendo a los problemas de palabras «numéricas», los números enteros consecutivos están a una unidad de distancia, por lo que los factores del producto (n + 2)! son de la forma:
1×2×3×4×…¡×(n – 1)×(n)×(n + 1)×(n + 2)
Al retroceder en la lista de factores hasta «n – 1», he creado una lista de factores que pueden anularse:
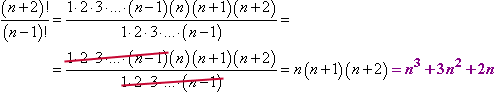
Toma nota de la forma en que manejé esa cancelación. Expandí las expresiones factoriales lo suficiente como para ver dónde podía cancelar los factores duplicados. Aunque no tenía ni idea de lo que podía ser n, podía cancelar. ¡Archiva esta técnica en tu cerebro, porque aunque no la necesites ahora, es casi seguro que la necesitarás más adelante.
Para obtener información sobre cómo encontrar el número de ceros al final de un factorial (como «¿Cuántos ceros hay al final de 23! después de multiplicarlo?»), mira esta nota.
Top | Volver al índice
|
Cite este artículo como: |
Stapel, Elizabeth. «Factoriales». Purplemath. Disponible en 2016
|
.