Objetivos de aprendizaje
Al final de esta sección, serás capaz de:
- Definir las fuerzas no conservativas y explicar cómo afectan a la energía mecánica.
- Mostrar cómo se puede aplicar el principio de conservación de la energía tratando las fuerzas conservativas en términos de sus energías potenciales y cualquier fuerza no conservativa en términos del trabajo que realizan.
Fuerzas no conservativas y fricción
Las fuerzas son conservativas o no conservativas. Las fuerzas conservativas fueron discutidas en Fuerzas conservativas y energía potencial. Una fuerza no conservativa es aquella en la que el trabajo depende del camino recorrido. La fricción es un buen ejemplo de fuerza no conservativa. Como se ilustra en la figura 1, el trabajo realizado contra el rozamiento depende de la longitud de la trayectoria entre los puntos inicial y final. Debido a esta dependencia de la trayectoria, no hay energía potencial asociada a las fuerzas no conservativas. Una característica importante es que el trabajo realizado por una fuerza no conservativa añade o quita energía mecánica a un sistema. La fricción, por ejemplo, crea energía térmica que se disipa, eliminando energía del sistema. Además, aunque la energía térmica sea retenida o captada, no puede volver a convertirse totalmente en trabajo, por lo que se pierde o no es recuperable también en ese sentido.

Figura 1. La cantidad de la cara feliz borrada depende del recorrido que haga la goma entre los puntos A y B, así como el trabajo realizado contra la fricción. Se realiza menos trabajo y se borra menos parte de la cara en la trayectoria de (a) que en la de (b). La fuerza aquí es la fricción, y la mayor parte del trabajo se convierte en energía térmica que posteriormente abandona el sistema (la cara feliz más el borrador). La energía gastada no puede recuperarse totalmente.
Cómo afectan las fuerzas no conservativas a la energía mecánica
La energía mecánica puede no conservarse cuando actúan fuerzas no conservativas. Por ejemplo, cuando un coche se detiene por rozamiento en un terreno llano, pierde energía cinética, que se disipa como energía térmica, reduciendo su energía mecánica. La figura 2 compara los efectos de las fuerzas conservativas y no conservativas. A menudo optamos por entender primero sistemas más sencillos como el descrito en la figura 2a antes de estudiar sistemas más complicados como el de la figura 2b.

Figura 2. Comparación de los efectos de las fuerzas conservativas y no conservativas sobre la energía mecánica de un sistema. (a) Un sistema con sólo fuerzas conservativas. Cuando se deja caer una roca sobre un muelle, su energía mecánica permanece constante (sin tener en cuenta la resistencia del aire) porque la fuerza del muelle es conservativa. El muelle puede impulsar la roca hasta su altura original, donde vuelve a tener sólo energía potencial debida a la gravedad. (b) Un sistema con fuerzas no conservativas. Cuando la misma roca se deja caer al suelo, es detenida por fuerzas no conservativas que disipan su energía mecánica como energía térmica, sonido y distorsión de la superficie. La roca ha perdido energía mecánica.
Cómo se aplica el teorema trabajo-energía
Ahora consideremos qué forma adopta el teorema trabajo-energía cuando actúan tanto fuerzas conservativas como no conservativas. Veremos que el trabajo realizado por las fuerzas no conservativas es igual al cambio en la energía mecánica de un sistema. Como se indica en La energía cinética y el teorema trabajo-energía, el teorema trabajo-energía establece que el trabajo neto en un sistema es igual al cambio en su energía cinética, o Wnet = ΔKE. El trabajo neto es la suma del trabajo de las fuerzas no conservativas más el trabajo de las fuerzas conservativas. Es decir,
Wnet = Wnc + Wc,
de modo que
Wnc + Wc = ΔKE,
donde Wnc es el trabajo total realizado por todas las fuerzas no conservativas y Wc es el trabajo total realizado por todas las fuerzas conservativas.

Figura 3. Una persona empuja una caja por una rampa, realizando un trabajo sobre la caja. La fricción y la fuerza gravitacional (no mostrada) también hacen trabajo sobre la caja; ambas fuerzas se oponen al empuje de la persona. A medida que la caja es empujada por la rampa, gana energía mecánica, lo que implica que el trabajo realizado por la persona es mayor que el trabajo realizado por la fricción.
Considere la Figura 3, en la que una persona empuja una caja por una rampa y se le opone la fricción. Al igual que en la sección anterior, observamos que el trabajo realizado por una fuerza conservativa proviene de una pérdida de energía potencial gravitacional, de modo que Wc = -ΔPE. Sustituyendo esta ecuación en la anterior y resolviendo para Wnc se obtiene
Wnc = ΔKE + ΔPE.
Esta ecuación significa que la energía mecánica total (KE + PE) cambia exactamente en la cantidad de trabajo realizado por las fuerzas no conservativas. En la figura 3, este es el trabajo realizado por la persona menos el trabajo realizado por la fricción. Por lo tanto, incluso si la energía no se conserva para el sistema de interés (como la caja), sabemos que se realizó una cantidad igual de trabajo para causar el cambio en la energía mecánica total.
Reorganizamos Wnc = ΔKE + ΔPE para obtener
KEi + PEi + Wnc = KEf + PEf.
Esto significa que la cantidad de trabajo realizado por las fuerzas no conservativas se suma a la energía mecánica de un sistema. Si Wnc es positivo, entonces la energía mecánica se incrementa, como cuando la persona empuja la caja por la rampa en la Figura 3. Si Wnc es negativo, la energía mecánica disminuye, como cuando la roca golpea el suelo en la figura 2b. Si Wnc es cero, la energía mecánica se conserva y las fuerzas no conservativas se equilibran. Por ejemplo, cuando se empuja una cortadora de césped a velocidad constante en un terreno llano, el trabajo realizado es eliminado por el trabajo de la fricción, y la cortadora tiene una energía constante.
Aplicando la conservación de la energía con fuerzas no conservativas
Cuando no se produce ningún cambio en la energía potencial, aplicar KEi + PEi + Wnc = KEf + PEf equivale a aplicar el teorema trabajo-energía estableciendo que el cambio en la energía cinética es igual al trabajo neto realizado sobre el sistema, que en el caso más general incluye tanto las fuerzas conservativas como las no conservativas. Pero cuando se busca, en cambio, encontrar un cambio en la energía mecánica total en situaciones que implican cambios tanto en la energía potencial como en la cinética, la ecuación anterior KE i + PEi + Wnc = KEf + PEf dice que se puede empezar por encontrar el cambio en la energía mecánica que habría resultado sólo de las fuerzas conservativas, incluyendo los cambios de energía potencial, y añadirle el trabajo realizado, con el signo adecuado, por cualquier fuerza no conservativa implicada.
Ejemplo 1. Calcular la distancia recorrida: Cuánto se desliza un jugador de béisbol
Considere la situación mostrada en la figura 4, en la que un jugador de béisbol se desliza hasta detenerse en un terreno llano. Utilizando consideraciones energéticas, calcule la distancia que el jugador de béisbol de 65,0 kg se desliza, dado que su velocidad inicial es de 6,00 m/s y la fuerza de fricción contra él es una constante de 450 N.

Figura 4. El jugador de béisbol se desliza hasta detenerse en una distancia d. En el proceso, la fricción elimina la energía cinética del jugador realizando una cantidad de trabajo igual a la energía cinética inicial.
Estrategia
La fricción detiene al jugador convirtiendo su energía cinética en otras formas, incluida la energía térmica. En términos del teorema trabajo-energía, el trabajo realizado por la fricción, que es negativo, se añade a la energía cinética inicial para reducirla a cero. El trabajo realizado por la fricción es negativo, porque f está en la dirección opuesta al movimiento (es decir, θ = 180º, y por tanto cos θ = -1). Por tanto, Wnc = -fd. La ecuación se simplifica a
rac{1}{2}{mv_{text{i}}^2-fd=0\
o
fd=frac{1}{2}{mv_{text{i}}^2\.
Ahora se puede resolver esta ecuación para la distancia d.
Solución
Resolviendo la ecuación anterior para d y sustituyendo los valores conocidos se obtiene
egin{array}{lll}d&&\frac{mv_{\text{i}}^2}{2f}\\\text{ }&&\frac{(65.0\text{ kg})(6,00\text{ m/s})^2}(2)(450\text{ N})}\\text{}&&2.60\texto{m}\pend{array}\\\N-
Discusión
El punto más importante de este ejemplo es que la cantidad de trabajo no conservativo es igual al cambio de energía mecánica. Por ejemplo, hay que trabajar más para detener un camión, con su gran energía mecánica, que para detener un mosquito.
Ejemplo 2. Cálculo de la distancia recorrida: Deslizándose por una pendiente
Suponga que el jugador del ejemplo 1 está corriendo por una colina que tiene una pendiente de 5,00º hacia arriba con una superficie similar a la del estadio de béisbol. El jugador se desliza con la misma velocidad inicial. Determina hasta dónde se desliza.

Figura 5. El mismo jugador de béisbol se desliza hasta detenerse en una pendiente de 5,00º.
Estrategia
En este caso, el trabajo realizado por la fuerza de rozamiento no conservativa sobre el jugador reduce la energía mecánica que tiene de su energía cinética a la altura cero, a la energía mecánica final que tiene al desplazarse por la distancia d para alcanzar la altura h a lo largo de la colina, con h = d sin 5,00º. Esto se expresa mediante la ecuación KE + PEi + Wnc = KE f + PEf.
Solución
El trabajo realizado por el rozamiento es de nuevo Wnc = -fd; inicialmente la energía potencial es PEi = mg – 0 = 0 y la energía cinética es \text{KE}_{text{i}=\frac{1}{2}mv_{text{i}^2\; las contribuciones energéticas finales son KEf = 0 para la energía cinética y PEf = mgh = mgd sin θ para la energía potencial.
Sustituyendo estos valores se obtiene
rac{1}{2}{mv_{text{i}}^2+0+\a la izquierda(-fd\right)=0+mgd\sin\theta
Resolver esto para d para obtener
egin{array}{lll}d&&\frac{\left(\frac{1}{2}\right)mv_{\text{i}}^2}{f+mg\sin\theta}\\&&\frac{(0.5)(65.0\text{ kg})(6.00\text{ m/s})^2}{450\text{ N}+(65.0\text{ kg})\ft(9.80\text{ m/s}^2\\right)\tecla(5.00^{\ccir})}{&&2.31\\N-texto{m}\Nfinalizar{array}\N-
Discusión
Como era de esperar, el jugador se desliza una distancia menor al deslizarse cuesta arriba. Nótese que el problema también podría haberse resuelto en términos de las fuerzas directamente y del teorema de la energía de trabajo, en lugar de utilizar la energía potencial. Este método habría requerido combinar los vectores fuerza normal y fuerza de gravedad, que ya no se cancelan entre sí porque apuntan en direcciones diferentes, y la fricción, para encontrar la fuerza neta. A continuación, se podría utilizar la fuerza neta y el trabajo neto para encontrar la distancia d que reduce la energía cinética a cero. Aplicando la conservación de la energía y utilizando la energía potencial en su lugar, sólo necesitamos considerar la energía potencial gravitatoria mgh, sin combinar y resolver los vectores de fuerza. Esto simplifica la solución considerablemente.
Haciendo Conexiones: Investigación para llevar a casa-Determinación de la fricción a partir de la distancia de parada
Este experimento implica la conversión de la energía potencial gravitatoria en energía térmica. Utiliza la regla, el libro y la canica de la sección «Haciendo Conexiones» de Energía Potencial Gravitacional. Además, necesitarás un vaso de espuma con un pequeño agujero en el lateral, como se muestra en la Figura 6. Desde la posición de 10 cm en la regla, deja que la canica ruede hacia el vaso situado en la parte inferior de la regla. Mide la distancia d que se desplaza la copa antes de detenerse. ¿Qué fuerzas han hecho que se detenga? ¿Qué ocurrió con la energía cinética de la canica en la parte inferior de la regla? A continuación, coloca la canica en las posiciones de 20 y 30 cm y mide de nuevo la distancia que recorre el vaso después de que la canica entre en él. Traza la distancia que se mueve la copa frente a la posición inicial de la canica en la regla. Es esta relación lineal?
Con algunas suposiciones sencillas, puedes usar estos datos para encontrar el coeficiente de fricción cinética μk de la taza sobre la mesa. La fuerza de rozamiento f sobre la taza es μkN, donde la fuerza normal N es sólo el peso de la taza más la canica. La fuerza normal y la fuerza de gravedad no realizan ningún trabajo porque son perpendiculares al desplazamiento de la taza, que se mueve horizontalmente. El trabajo realizado por la fricción es fd. Necesitarás también la masa de la canica para calcular su energía cinética inicial.
Es interesante hacer el experimento anterior también con una canica de acero (o cojinete de bolas). Al soltarla desde las mismas posiciones de la regla que hiciste con la canica de vidrio, ¿la velocidad de esta canica de acero es la misma que la de la canica de la parte inferior de la regla? ¿Es la distancia que recorre la copa proporcional a la masa de las canicas de acero y de vidrio?

Figura 6. Haciendo rodar una canica por una regla hasta un vaso de espuma.
Exploraciones de PhET: La rampa
Explora las fuerzas, la energía y el trabajo mientras empujas objetos domésticos hacia arriba y hacia abajo en una rampa. Baja y sube la rampa para ver cómo el ángulo de inclinación afecta a las fuerzas paralelas que actúan sobre el archivador. Los gráficos muestran las fuerzas, la energía y el trabajo.
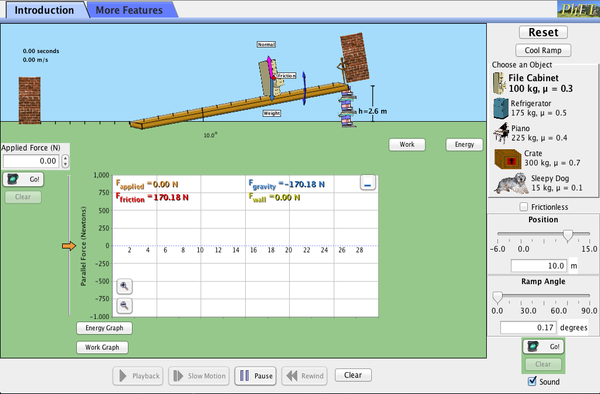
Haz clic para descargar. Run using Java.
Resumen de la sección
- Una fuerza no conservativa es aquella para la que el trabajo depende de la trayectoria.
- La fricción es un ejemplo de fuerza no conservativa que cambia la energía mecánica en energía térmica.
- El trabajo Wnc realizado por una fuerza no conservativa cambia la energía mecánica de un sistema. En forma de ecuación, Wnc = ΔKE + ΔPE o, de forma equivalente, KEi + PEi + Wnc = KEf + PEf.
- Cuando actúan tanto fuerzas conservativas como no conservativas, se puede aplicar la conservación de la energía y utilizarla para calcular el movimiento en términos de las energías potenciales conocidas de las fuerzas conservativas y el trabajo realizado por las fuerzas no conservativas, en lugar de encontrar el trabajo neto a partir de la fuerza neta, o tener que aplicar directamente las leyes de Newton.
Problemas &
- Un esquiador de 60,0 kg con una velocidad inicial de 12,0 m/s sube a toda velocidad por una subida de 2,50 m de altura como se muestra en la figura 7. Encuentra su velocidad final en la cima, dado que el coeficiente de fricción entre sus esquís y la nieve es de 0.0800. (Sugerencia: Encuentre la distancia recorrida por la pendiente suponiendo una trayectoria en línea recta como se muestra en la figura.)

Figura 7. La energía cinética inicial del esquiador se utiliza parcialmente en el desplazamiento por inercia hasta la cima de una subida.
- (a) ¿A qué altura puede subir por inercia un coche (con el motor desembragado) si el trabajo realizado por el rozamiento es despreciable y su velocidad inicial es de 110 km/h? (b) Si, en la realidad, se observa que un coche de 750 kg con una velocidad inicial de 110 km/h sube por inercia una colina hasta una altura de 22,0 m por encima de su punto de partida, ¿cuánta energía térmica se ha generado por el rozamiento? c) ¿Cuál es la fuerza media de rozamiento si la colina tiene una pendiente de 2,5º sobre la horizontal?

Figura 7. La energía cinética inicial del esquiador se utiliza parcialmente en el desplazamiento por inercia hasta la cima de una subida.
Glosario
Fuerza no conservativa: fuerza cuyo trabajo depende del camino seguido entre las configuraciones inicial y final dadas
Fricción: la fuerza entre superficies que se opone al deslizamiento de una sobre la otra; el rozamiento transforma la energía mecánica en energía térmica
Soluciones seleccionadas de problemas &
1. 9,46 m/s