⇐ Tema anterior|Tema siguiente ⇒ Tabla de contenidos
Antes de realizar un experimento, debe realizar un análisis de potencia para estimar el número de observaciones que necesita para tener una buena oportunidad de detectar el efecto que está buscando.
Introducción
Cuando esté diseñando un experimento, es una buena idea estimar el tamaño de la muestra que necesitará. Esto es especialmente cierto si se propone hacer algo doloroso a los seres humanos u otros vertebrados, donde es particularmente importante minimizar el número de individuos (sin que el tamaño de la muestra sea tan pequeño que todo el experimento sea una pérdida de tiempo y sufrimiento), o si está planeando un experimento que consume mucho tiempo o es costoso. Se han desarrollado métodos para muchas pruebas estadísticas con el fin de estimar el tamaño de la muestra necesario para detectar un efecto concreto, o para estimar el tamaño del efecto que puede detectarse con un tamaño de muestra concreto.
Para realizar un análisis de potencia, es necesario especificar un tamaño del efecto. Este es el tamaño de la diferencia entre su hipótesis nula y la hipótesis alternativa que espera detectar. Para la investigación biológica aplicada y clínica, puede haber un tamaño del efecto muy definido que desee detectar. Por ejemplo, si está probando un nuevo champú para perros, el departamento de marketing de su empresa puede decirle que la producción del nuevo champú sólo merecería la pena si hiciera que el pelaje de los perros fuera al menos un 25% más brillante, de media. Ese sería su tamaño del efecto, y lo utilizaría al decidir cuántos perros necesitaría pasar por el reflectómetro canino.
Cuando se realiza una investigación biológica básica, a menudo no se sabe cuán grande es la diferencia que se busca, y la tentación puede ser simplemente utilizar el mayor tamaño de muestra que pueda permitirse, o utilizar un tamaño de muestra similar al de otras investigaciones en su campo. Aun así, deberías hacer un análisis de potencia antes de hacer el experimento, sólo para tener una idea de qué tipo de efectos podrías detectar. Por ejemplo, algunos chiflados antivacunas han propuesto que el gobierno de EE.UU. lleve a cabo un gran estudio de niños vacunados y no vacunados para ver si las vacunas causan autismo. No está claro qué tamaño de efecto sería interesante: ¿Un 10% más de autismo en un grupo? ¿un 50% más? ¿el doble? Sin embargo, un análisis de potencia muestra que incluso si el estudio incluyera a todos los niños no vacunados de Estados Unidos de entre 3 y 6 años, y un número igual de niños vacunados, tendría que haber un 25% más de autismo en un grupo para tener una alta probabilidad de ver una diferencia significativa. Un estudio más plausible, de 5.000 niños no vacunados y 5.000 vacunados, detectaría una diferencia significativa con alta potencia sólo si hubiera tres veces más autismo en un grupo que en el otro. Dado que es poco probable que haya una diferencia tan grande en el autismo entre los niños vacunados y los no vacunados, y dado que no encontrar una relación con un estudio de este tipo no convencería a los chiflados de la vacunación de que no hay ninguna relación (nada les convencería de que no hay ninguna relación, eso es lo que les convierte en chiflados), el análisis de potencia te dice que un estudio tan grande y caro no merecería la pena.
Parámetros
Hay cuatro o cinco números involucrados en un análisis de potencia. Debe elegir los valores de cada uno antes de hacer el análisis. Si no tiene una buena razón para usar un valor en particular, puede probar diferentes valores y observar el efecto en el tamaño de la muestra.
Tamaño del efecto
El tamaño del efecto es la desviación mínima de la hipótesis nula que espera detectar. Por ejemplo, si está tratando a las gallinas con algo que espera que cambie la proporción de sexos de sus polluelos, podría decidir que el cambio mínimo en la proporción de sexos que está buscando es del 10%. Se diría entonces que el tamaño del efecto es del 10%. Si está probando algo para que las gallinas pongan más huevos, el tamaño del efecto podría ser de 2 huevos al mes.
Ocasionalmente, tendrá una buena razón económica o clínica para elegir un tamaño del efecto particular. Si está probando un suplemento alimenticio para gallinas que cuesta 1,50 dólares al mes, sólo le interesa averiguar si producirá más de 1,50 dólares de huevos extra cada mes; saber que un suplemento produce 0,1 huevos extra al mes no es una información útil para usted, y no necesita diseñar su experimento para averiguarlo. Pero para la mayor parte de la investigación biológica básica, el tamaño del efecto no es más que un bonito número redondo que te has sacado de la manga. Digamos que estás haciendo un análisis de potencia para un estudio de una mutación en una región promotora, para ver si afecta a la expresión génica. ¿Qué tan grande es el cambio en la expresión del gen que estás buscando? 10%? 20%? 50%? Es un número bastante arbitrario, pero tendrá un efecto enorme en el número de ratones transgénicos que darán sus caras vidas por su ciencia. Si no tiene una buena razón para buscar un tamaño del efecto en particular, podría admitirlo y dibujar un gráfico con el tamaño de la muestra en el eje X y el tamaño del efecto en el eje Y. G*Power lo hará por usted.
Alpha
Alpha es el nivel de significación de la prueba (el valor P), la probabilidad de rechazar la hipótesis nula aunque sea verdadera (un falso positivo). El valor habitual es alfa=0,05. Algunas calculadoras de potencia utilizan el alfa de una cola, lo cual es confuso, ya que el alfa de dos colas es mucho más común. Asegúrese de saber cuál está utilizando.
Beta o potencia
Beta, en un análisis de potencia, es la probabilidad de aceptar la hipótesis nula, aunque sea falsa (un falso negativo), cuando la diferencia real es igual al tamaño del efecto mínimo. La potencia de una prueba es la probabilidad de rechazar la hipótesis nula (obtener un resultado significativo) cuando la diferencia real es igual al tamaño mínimo del efecto. La potencia es 1-beta. No hay un consenso claro sobre el valor a utilizar, por lo que es otro número que se saca de la manga; una potencia del 80% (equivalente a una beta del 20%) es probablemente la más común, mientras que algunas personas utilizan el 50% o el 90%. El coste de un falso negativo debería influir en la elección de la potencia; si realmente quiere estar seguro de que detecta el tamaño del efecto, querrá utilizar un valor más alto de potencia (beta más bajo), lo que dará lugar a un tamaño de muestra mayor. Algunas calculadoras de potencia le piden que introduzca la beta, mientras que otras piden la potencia (1-beta); asegúrese de que entiende cuál debe utilizar.
Desviación estándar
Para las variables de medición, también necesita una estimación de la desviación estándar. A medida que la desviación estándar se hace más grande, se hace más difícil detectar una diferencia significativa, por lo que necesitará un tamaño de muestra más grande. Su estimación de la desviación estándar puede provenir de experimentos piloto o de experimentos similares en la literatura publicada. Es poco probable que su desviación estándar una vez que realice el experimento sea exactamente la misma, por lo que su experimento será en realidad algo más o menos potente de lo que había predicho.
Para las variables nominales, la desviación estándar es una función simple del tamaño de la muestra, por lo que no necesita estimarla por separado.
Cómo funciona
Los detalles de un análisis de potencia son diferentes para las diferentes pruebas estadísticas, pero los conceptos básicos son similares; aquí utilizaré la prueba binomial exacta como ejemplo. Imagínese que está estudiando las fracturas de muñeca y su hipótesis nula es que la mitad de las personas que se rompen una muñeca se rompen la derecha y la otra mitad se rompen la izquierda. Usted decide que el tamaño mínimo del efecto es del 10%; si el porcentaje de personas que se rompen la muñeca derecha es del 60% o más, o del 40% o menos, quiere tener un resultado significativo de la prueba binomial exacta. No tengo ni idea de por qué has elegido el 10%, pero eso es lo que usarás. El alfa es el 5%, como siempre. Quieres que la potencia sea del 90%, lo que significa que si el porcentaje de muñecas derechas rotas es realmente del 40% o del 60%, quieres un tamaño de muestra que dé un resultado significativo (P<0,05) el 90% de las veces, y un resultado no significativo (que sería un falso negativo en este caso) sólo el 10% de las veces.
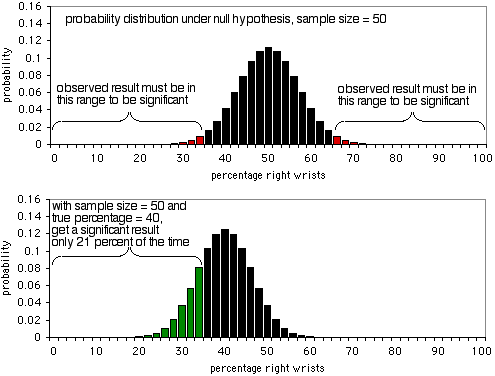

La primera gráfica muestra la distribución de probabilidad bajo la hipótesis nula con un tamaño de muestra de 50 individuos. Si la hipótesis nula es verdadera, se verá que menos del 36% o más del 64% de las personas se rompen la muñeca derecha (un falso positivo) aproximadamente el 5% de las veces. Como muestra el segundo gráfico, si el porcentaje verdadero es del 40%, los datos de la muestra serán inferiores al 36 o superiores al 64% sólo el 21% de las veces; obtendrá un verdadero positivo sólo el 21% de las veces, y un falso negativo el 79% de las veces. Obviamente, un tamaño de muestra de 50 es demasiado pequeño para este experimento; sólo daría un resultado significativo el 21% de las veces, incluso si hay una proporción de 40:60 de muñecas derechas rotas con respecto a las izquierdas.
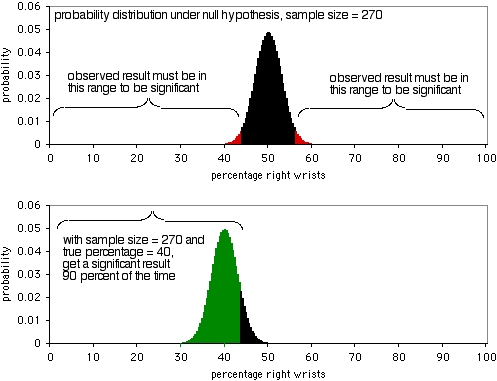

La siguiente gráfica muestra la distribución de probabilidad bajo la hipótesis nula con un tamaño de muestra de 270 individuos. Para que sea significativa al nivel P<0,05, el resultado observado tendría que ser inferior al 43,7% o superior al 56,3% de las personas que se rompen la muñeca derecha. Como muestra el segundo gráfico, si el porcentaje real es del 40%, los datos de la muestra serán así de extremos el 90% de las veces. Un tamaño de muestra de 270 es bastante bueno para este experimento; daría un resultado significativo el 90% de las veces si hay una proporción de 40:60 de muñecas derechas rotas respecto a las izquierdas. Si la proporción de muñecas derechas e izquierdas rotas se aleja más de 50:50, tendrá una probabilidad aún mayor de obtener un resultado significativo.
Ejemplos
Usted planea cruzar guisantes que son heterocigotos para el color amarillo/verde de los guisantes, donde el amarillo es dominante. La proporción esperada en la descendencia es 3 Amarillo: 1 verde. Usted quiere saber si los guisantes amarillos son realmente más o menos aptos, lo que podría manifestarse como una proporción de guisantes amarillos diferente a la esperada. Decide arbitrariamente que quiere un tamaño de muestra que detecte una diferencia significativa (P<0,05) si hay un 3% más o menos de guisantes amarillos de lo esperado, con una potencia del 90%. Usted probará los datos utilizando la prueba binomial exacta de bondad de ajuste si el tamaño de la muestra es lo suficientemente pequeño, o una prueba G de bondad de ajuste si el tamaño de la muestra es mayor. El análisis de potencia es el mismo para ambas pruebas.
Usando G*Power como se describe para la prueba exacta de bondad de ajuste, el resultado es que se necesitarían 2109 plantas de guisantes si se quiere obtener un resultado significativo (P<0,05) el 90% de las veces, si la verdadera proporción de guisantes amarillos es del 78%, y 2271 guisantes si la verdadera proporción es del 72% de amarillos. Como te interesa una desviación en cualquier dirección, utilizas el número mayor, 2271. Son muchos guisantes, pero te tranquiliza ver que no es un número ridículo. Si quieres detectar una diferencia del 0,1% entre el número esperado y el observado de guisantes amarillos, puedes calcular que necesitarás 1.970.142 guisantes; si eso es lo que necesitas detectar, el análisis del tamaño de la muestra te dice que vas a tener que incluir un robot clasificador de guisantes en tu presupuesto.
Los datos de ejemplo para la prueba t de dos muestras muestran que la altura media en la sección de las 14 horas de Análisis de Datos Biológicos fue de 66,6 pulgadas y la altura media en la sección de las 17 horas fue de 64,6 pulgadas, pero la diferencia no es significativa (P=0,207). Usted quiere saber cuántos estudiantes tendría que muestrear para tener un 80% de posibilidades de que una diferencia tan grande sea significativa. Utilizando G*Power como se describe en la página de la prueba t de dos muestras, introduce 2,0 para la diferencia de medias. Utilizando la función STDEV en Excel, calcule la desviación estándar para cada muestra en los datos originales; es 4,8 para la muestra 1 y 3,6 para la muestra 2. Introduzca 0,05 para alfa y 0,80 para potencia. El resultado es 72, lo que significa que si los estudiantes de las 5 p.m. fueran realmente 5 centímetros más bajos que los de las 2 p.m., necesitarías 72 estudiantes en cada clase para detectar una diferencia significativa el 80% de las veces, si la diferencia real es de 5 centímetros.
Cómo hacer análisis de potencia
G*Power
G*Power es un excelente programa gratuito, disponible para Mac y Windows, que hará análisis de potencia para una gran variedad de pruebas. Explicaré cómo utilizar G*Power para los análisis de potencia para la mayoría de las pruebas en este manual.
R
Salvatore Mangiafico’s R Companion tiene programas R de ejemplo para hacer análisis de potencia para muchas de las pruebas en este manual; vaya a la página de la prueba individual y desplácese hasta la parte inferior para el programa de análisis de potencia.
SAS
SAS tiene un PROC POWER que se puede utilizar para los análisis de potencia. Se introducen los parámetros necesarios (que varían dependiendo de la prueba) y se introduce un período (que simboliza los datos que faltan en SAS) para el parámetro que se está resolviendo (normalmente ntotal, el tamaño total de la muestra, o npergroup, el número de muestras en cada grupo). Me parece que G*Power es más fácil de usar que SAS para este propósito, por lo que no recomiendo el uso de SAS para sus análisis de potencia.
⇐ Tema anterior|Tema siguiente ⇒ Tabla de contenidos
Esta página fue revisada por última vez el 20 de julio de 2015. Su dirección es http://www.biostathandbook.com/power.html. Puede citarse como:
McDonald, J.H. 2014. Manual de estadística biológica (3ª ed.). Sparky House Publishing, Baltimore, Maryland. Esta página web contiene el contenido de las páginas 40-44 de la versión impresa.
©2014 por John H. McDonald. Probablemente pueda hacer lo que quiera con este contenido; consulte la página de permisos para más detalles.