

En el año 1072 d.C., Omar Khayyam documentó la duración del año más exacta jamás calculada, una cifra que sigue siendo lo suficientemente precisa para la mayoría de los propósitos del mundo moderno. Khayyam fue astrónomo, astrólogo, médico, filósofo y matemático: realizó destacadas contribuciones en álgebra. Su poesía es más conocida en Occidente que la de cualquier otro poeta no occidental.
El hombre en sí mismo sigue siendo una especie de enigma. Diferentes biógrafos lo han documentado como un agnóstico amante de la diversión y bebedor de vino; un zoroastriano oculto; un musulmán sufí; un musulmán suní ortodoxo; y un seguidor de la filosofía de la antigua Grecia. Todos coinciden en que fue un intelectual excepcional.
Inicios
Omar Khayyam nació el 18 de mayo de 1048 en la gran ciudad comercial de Nishapur, en el norte de Persia. Hoy la ciudad se encuentra en Irán. El padre de Omar era Ebrahim Khayyami, un médico rico. No se conoce el nombre de la madre de Omar. Algunos autores han escrito que el padre de Omar se ganaba la vida fabricando tiendas, ya que Khayyami significa fabricante de tiendas. Sin embargo, aunque muchos anglosajones se apelliden Smith, no significa que sus padres se pasaran el día martilleando metal caliente en un yunque.
La familia de Omar era musulmana. Su padre parece haberse relajado con respecto a la religión, empleando a un matemático llamado Bahmanyar bin Marzban, un devoto de la antigua religión persa del zoroastrismo, como tutor de Omar. Bahmanyar había sido alumno del gran médico, científico y filósofo Avicena, y le dio a Omar una educación completa en ciencia, filosofía y matemáticas. Khawjah al-Anbari enseñó a Omar astronomía, guiándolo a través del Almagesto de Ptolomeo.
En su temprana adolescencia Omar trabajó en el consultorio de su padre aprendiendo sobre medicina.
Omar Khayyam celebró su decimoctavo cumpleaños en 1066. Ese mismo año, el cometa Halley apareció en los cielos, el ejército normando de Guillermo el Conquistador invadió Inglaterra y el padre de Omar, Ebrahim, murió. Unos meses después de la muerte de Ebrahim, el tutor de Omar, Bahmanyar, también murió.
Era el fin de una era en la vida de Omar Khayyam. Era el momento de poner en orden los asuntos de su familia y seguir adelante.
Samarkanda
Omar Khayyam se unió a una de las caravanas regulares que hacían un viaje de tres meses desde Nishapur a la gran ciudad de Samarkanda, que ahora está en Uzbekistán. Samarcanda era un centro de erudición, y Khayyam llegó allí probablemente en 1068, con 20 años de edad.
En Samarcanda entró en contacto con el viejo amigo de su padre, Abu Tahir, que era gobernador y juez principal de la ciudad. Tahir, al observar el extraordinario talento de Khayyam con los números, le dio trabajo en su oficina. Pronto Khayyam recibió un trabajo en la tesorería del rey.
Mientras vivía en Samarcanda, Khayyam hizo un gran avance en el álgebra.
Contribuciones de Omar Khayyam a la ciencia
Álgebra
En la escuela secundaria aprendemos sobre ecuaciones de la forma ax2 + bx + c = 0; éstas se llaman ecuaciones cuadráticas. Las ecuaciones cúbicas son de la forma ax3 + bx2 + cx + d = 0. Naturalmente, las ecuaciones cúbicas son más difíciles de resolver que las cuadráticas.
Khayyam conjeturó correctamente que no es posible resolver las ecuaciones cúbicas utilizando las herramientas geométricas tradicionales de la Antigua Grecia, la regla y el compás. Se necesitan otros métodos.
A la edad de 22 años, en 1070, Khayyam publicó una de sus mayores obras: Tratado sobre la Demostración de Problemas de Álgebra y Equilibrio. En él demostró que una ecuación cúbica puede tener más de una solución. También demostró que las intersecciones de las secciones cónicas, como las parábolas y los círculos, pueden utilizarse para obtener soluciones geométricas de las ecuaciones cúbicas. En realidad, Arquímedes había empezado a trabajar en este campo más de mil años antes, cuando consideró el problema específico de encontrar la relación entre el volumen de una parte de una esfera y otra. Khayyam consideró el problema de una manera más general y metódica.
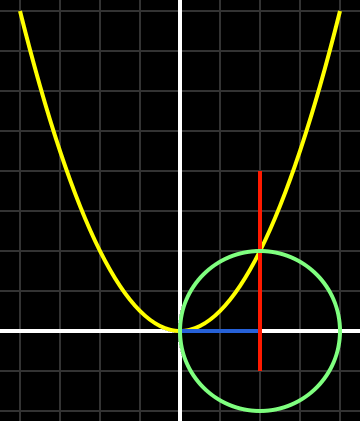
En el lenguaje de la matemática moderna, la solución de Khayyam a la ecuación x3 + a2x = b presenta una parábola de ecuación x2 = ay, un círculo de diámetro b/a2 y una línea vertical que pasa por el punto de intersección. La solución viene dada por la distancia en el eje x entre el origen y la línea vertical (roja). Imagen de Pieter Kuiper.
Las soluciones de Khayyam evitaban los coeficientes negativos y las raíces negativas porque los números negativos no estaban reconocidos en las matemáticas islámicas. (Sin embargo, algunas culturas habían incorporado los números negativos a las matemáticas; por ejemplo, Brahmagupta había introducido los números negativos en las matemáticas indias 400 años antes.)
Aunque el logro de Khayyam fue magnífico, se sintió personalmente decepcionado por tener que utilizar la geometría para resolver las ecuaciones cúbicas; había esperado descubrir un algoritmo utilizando sólo el álgebra.
El Tratado sobre la Demostración de Problemas de Álgebra y Equilibrio estableció a Khayyam como un matemático de primer rango, y su reputación se extendió rápidamente por toda Persia.
Después del avance de Khayyam hubo pocos progresos significativos en las ecuaciones cúbicas hasta 1535, cuando Niccolo Tartaglia encontró soluciones generales para todas las ecuaciones cúbicas.
El álgebra de Khayyam no era el sistema de letras y signos que usamos hoy en día. Su álgebra se expresaba en palabras. Así, donde hoy escribimos:
Resolver para x:
x2 + 6 = 5x
Khayyam escribió: ¿Cuál es la cantidad de un cuadrado para que al sumarle 6 dirhams se haga igual a cinco raíces de ese cuadrado?
Enlazando Álgebra y Geometría
El Álgebra y la Geometría fueron enlazadas con éxito por Pierre de Fermat y René Descartes en la década de 1600, dando lugar al moderno sistema de coordenadas x-y.
El trabajo de Khayyam con los cúbicos le hizo estar seguro de que el álgebra y la geometría estaban vinculadas, y citó los Elementos de Euclides para apoyar la idea:
Quien piense que el álgebra es un truco para obtener incógnitas ha pensado en vano. No hay que prestar atención al hecho de que el álgebra y la geometría son diferentes en apariencia. Las álgebras son hechos geométricos que se demuestran en las proposiciones 5 y 6 del libro 2 de los Elementos de Euclides.
Longitud del año
En 1073, Khayyam recibió una invitación a la ciudad persa de Isfahan, capital del Imperio Selyúcida, para que preparara un calendario que funcionara de forma ordenada y fuera preciso para siempre -esta era una época en la que las longitudes de los años cambiaban regularmente-.
La invitación de Khayyam provino de los dos hombres más poderosos del Imperio Selyúcida, del que formaba parte Persia: se trataba de Malik Shah, sultán del imperio, y Nizam al-Mulk, su visir.
Khayyam reclutó a otros científicos de talento para que le acompañaran a Isfahan en 1074. Allí recibió un salario extraordinariamente alto y disfrutó de un estilo de vida privilegiado. Malik Shah pagó a Khayyam para que fundara un observatorio con el objetivo inicial de realizar observaciones de los cielos durante 30 años, tiempo en el que Saturno, el planeta más lejano entonces conocido, completaría una órbita.
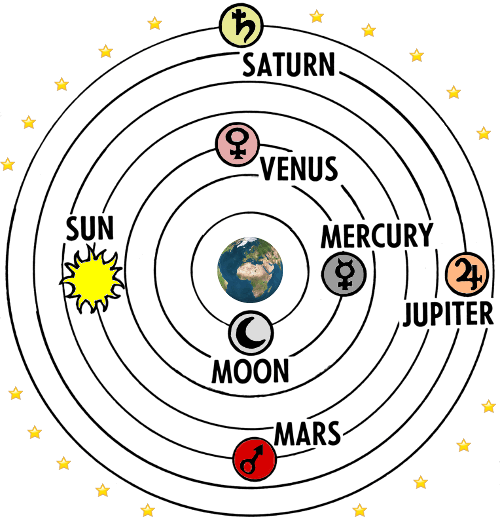
El universo de Ptolomeo: el modelo aceptado por Omar Khayyam.
Durante su estancia en Isfahan, Khayyam midió la duración de un año -en concreto, la duración del año tropical- con notable exactitud y precisión.
Khayyam descubrió que 1.029.983 días hacían 2.820 años. Esto da una duración del año tropical de 365,2422 días con siete cifras significativas. Aunque se ha puesto de moda citar más decimales que esto, la entrada de Khayyam de 1.029.983 días contiene siete cifras significativas, por lo que no es razonable citar más de este número de cifras significativas en la longitud del año calculado.
Hoy sabemos que la longitud de un año tropical en realidad cambia hasta 30 minutos de un año a otro. La duración media del año tropical citada hoy es de 365,242189 días, que con siete cifras significativas es de 365,2422 días, exactamente la cifra a la que llegó Khayyam hace casi mil años. La duración de un año tropical también aumenta muy ligeramente con el paso del tiempo, aunque no lo suficiente entre la época de Khayyam y la nuestra como para que se note en una escala de siete cifras significativas.
Malik Shah introdujo el nuevo calendario de Khayyam en el Imperio Selyúcida el 15 de marzo de 1079. Se utilizó hasta el siglo XX.
El Postulado Paralelo
Los 13 libros de los Elementos de Euclides publicados en torno al año 300 a.C. fueron probablemente los libros más influyentes de toda la historia de las matemáticas. Los Elementos se habían construido sobre cinco postulados geométricos, es decir, cinco cosas que se suponían ciertas sobre la geometría: por ejemplo, todos los ángulos rectos son iguales entre sí.
El quinto de los cinco postulados de Euclides era el postulado del paralelo. El postulado de las paralelas resultó ser una fuente de desconcierto, irritación y alegría para los matemáticos durante milenios. La alegría solía durar poco, ya que pertenecía a los matemáticos que creían haber demostrado el postulado sólo para decepcionarse cuando se identificaba un error en su «prueba».
Euclides había considerado una línea recta que cruzaba otras dos líneas rectas. Se fijó en la situación en la que los ángulos interiores (mostrados en la imagen inferior) suman menos de 180 grados. En estas circunstancias, dijo que las dos rectas acabarán encontrándose en el lado de los dos ángulos que suman menos de 180 grados.
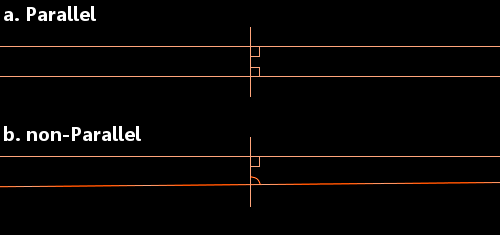
a. Cuando cada ángulo es de 90 grados, las líneas son paralelas.
b. Si uno o ambos ángulos son menores de 90 grados, las rectas se encontrarán.
Desde que se publicaron por primera vez los Elementos, los matemáticos habían intentado utilizar los cuatro primeros postulados de Euclides para demostrar el postulado de las paralelas. Estaban condenados a fracasar. Ahora sabemos que es imposible demostrar el postulado del paralelo utilizando los otros postulados de Euclides.
El intento de Omar Khayyam fue interesante. En su Explicación de las dificultades de los postulados de los elementos de Euclides pide a sus lectores que consideren una línea recta AB:


Pide a sus lectores que consideren dos líneas iguales que son perpendiculares a AB y ve tres posibles disposiciones, que pueden producir figuras de cuatro lados:


A continuación refuta la posibilidad de que los ángulos C y/o D puedan ser otra cosa que ángulos rectos y en la imagen de arriba sólo es posible la opción central. Así, cree haber demostrado el postulado de las paralelas. En realidad, no lo ha hecho, lo único que ha hecho es enunciarlo de una manera diferente.
Lo interesante para los historiadores de las matemáticas es que en las ideas de Khayyam -que se muestran a grandes rasgos en las imágenes de arriba- pueden ver los primeros destellos de la geometría no euclidiana.
Algunos detalles personales y el final
No se conocen detalles completos de la vida personal de Khayyam. Se cree que se casó y que tuvo al menos un hijo y una hija.
En 1092, Malik Shah y su visir murieron, el primero probablemente por envenenamiento y el segundo por asesinato. Khayyam se escondió durante la consiguiente lucha por el poder. Su supervivencia dependía de pasar desapercibido. Había sido el médico personal de Malik Shah y se había convertido en su amigo personal, lo que le había granjeado enemigos, y la poesía de Khayyam sugiere que su comportamiento podría no haber sido devotamente religioso, lo que también le había granjeado enemigos. En realidad, Khayyam no publicó ninguna poesía en vida. Algunas de sus cavilaciones habrían puesto potencialmente en peligro su vida.
Después de la lucha por el poder, Khayyam tardó unos 20 años en rehabilitarse por completo y en volver a surgir, a los 64 años, en compañía de gente poderosa. Sin embargo, se negó a enseñar. Uno de sus poemas sugiere el por qué de esto:
No pueden ser contados por miedo a perder la cabeza;
Ya que nadie es apto para aprender, o se preocupa por saber,
Es mejor que todos mis pensamientos permanezcan sin decir.
Omar Khayyam murió a la edad de 83 años en su ciudad natal de Nishapur el 4 de diciembre de 1131. Fue enterrado en una tumba cuyo emplazamiento había elegido en un huerto en el que florecía dos veces al año.
La poesía de Khayyam se popularizó en el siglo XIX gracias a las traducciones de Edward FitzGerald en las Rubaiyat de Omar Khayyam. Khayyam llegó a ser tan admirado en Occidente que en 1963 el Sha de Irán hizo exhumar su tumba y trasladar los restos de Khayyam a un enorme mausoleo construido a tal efecto en Nishapur, donde los turistas podían rendir homenaje al gran poeta.
Terminaremos con una de las cuartetas más famosas y evocadoras de Khayyam:
Una jarra de vino, una hogaza de pan-y tú
A mi lado cantando en el desierto-
Y el desierto es el paraíso.»
Autor de esta página: The Doc
Imágenes mejoradas digitalmente y coloreadas por esta web. © Todos los derechos reservados.
Cite esta página
Por favor, utilice la siguiente cita conforme a MLA:
"Omar Khayyam." Famous Scientists. famousscientists.org. 5 Nov. 2016. Web. <www.famousscientists.org/omar-khayyam/>.
Publicado por FamousScientists.org
Más lecturas
Edward FitzGerald (traductor)
El Rubaiyat de Omar Khayyam
Howard Willford Bell, 1901
Victor J. Katz
Una historia de las matemáticas: An Introduction
HarperCollins College Publishers, New York, 1993
Roshdi Rashed (Editor)
Enciclopedia de la Historia de la ciencia árabe
Routledge, 1996
Historia de la Astronomía – Oriente Medio
ephemeris.com, 2003
Hazhir Teimourian
Omar Khayyam: Poeta, rebelde, astrónomo
The History Press, 2008
Mehdi Aminrazavi
El vino de la sabiduría: La vida, la poesía y la filosofía de Omar Khayyam
Oneworld Publications, 2013