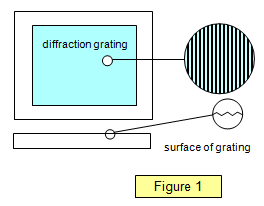
Si el número de rendijas de un obstáculo es grande, la nitidez del patrón mejora, estrechándose los máximos. Los obstáculos con un gran número de rendijas (más de 20 al milímetro, por ejemplo) se denominan rejillas de difracción. Estas fueron desarrolladas por primera vez por Fraunhofer a finales del siglo XVIII y consistían en un fino hilo de plata enrollado en dos tornillos paralelos que daban unos 30 obstáculos al milímetro. n 1882, Rowland utilizó un diamante para trazar finas líneas en el cristal, con las crestas actuando como rendijas y las reglas como obstáculos (véase la figura 1). Utilizando este método es posible obtener rejillas de difracción con hasta 3000 líneas por milímetro, aunque las rejillas «gruesas» con unas 500 líneas por milímetro son mejores para el uso general.
En muchas escuelas se utilizan habitualmente dos tipos, uno con 300 líneas por mm y otro con 80 líneas por mm.
También se utilizan rejillas de reflexión, en las que la imagen difractada se ve después de la reflexión desde una superficie reglada. Un muy buen ejemplo de rejilla de difracción por reflexión es un CD. Un DVD con reglas más finas da un patrón de difracción mucho más amplio.
La teoría de ondas y la rejilla de difracción
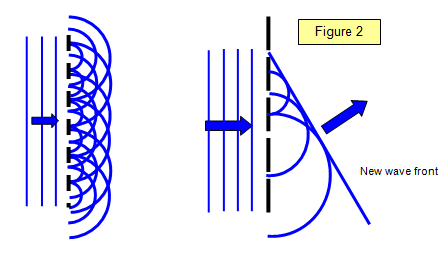
La figura 2 muestra la construcción de Huygens para una rejilla. Se puede ver cómo las ondas circulares difractadas de cada rendija se suman en ciertas direcciones para dar una onda difractada que tiene un frente de onda plano al igual que las ondas que golpean la rejilla desde la izquierda. Esta onda plana se forma dibujando la línea que se encuentra con todas las pequeñas ondas circulares y se denomina envolvente de todas estas pequeñas ondas secundarias.
La fórmula de la rejilla de difracción
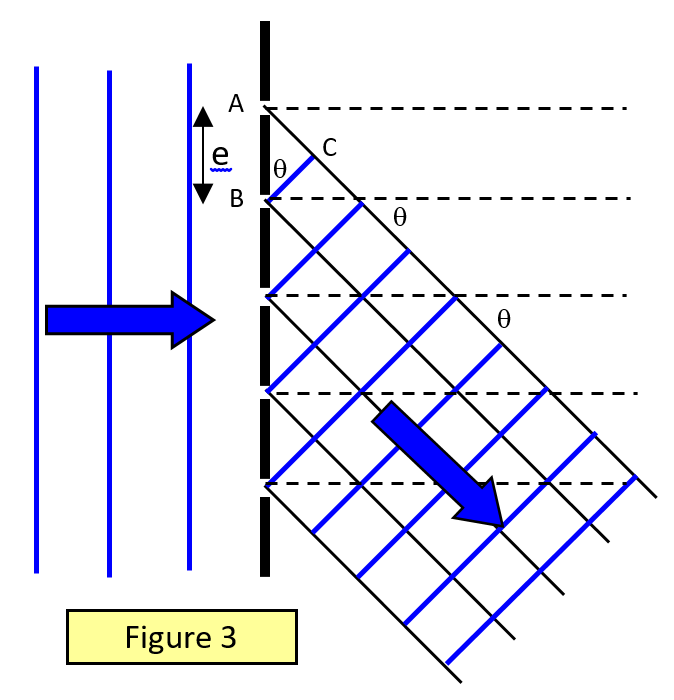
Consideremos un haz de luz paralelo que incide normalmente sobre una rejilla de difracción con una separación de rejilla e (la separación de rejilla es la inversa del número de líneas por unidad de longitud). Consideremos la luz que se difracta con un ángulo q respecto a la normal y que procede de puntos correspondientes de rendijas adyacentes (figura 3).
Para un máximo la diferencia de trayectoria = AC = mλ
Pero AC = e sinθ. Por tanto, para un máximo:
mλ = e sinθ
donde m = 0, 1, 2,3…
El número m se conoce como el orden del espectro, es decir, se forma un espectro de primer orden para m = 1, y así sucesivamente.
Si se utiliza luz de una sola longitud de onda, como la de un láser, entonces se produce una serie de líneas nítidas, una línea para cada orden del espectro. Con una fuente de luz blanca se forma una serie de espectros en los que la luz de menor longitud de onda tiene el menor ángulo de difracción.
Al derivar la fórmula anterior, hemos supuesto que el haz incidente está en ángulo recto con la cara de la rejilla. Hay que tener en cuenta si no es así. La forma más sencilla es medir la posición del espectro de primer orden a cada lado del centro, registrar el ángulo entre estas posiciones y luego dividirlo a la mitad, como se muestra en la Figura 4.
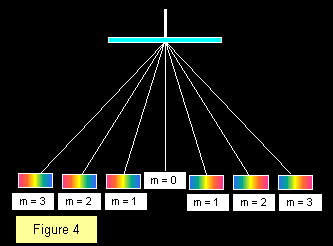
El número de órdenes de espectros visibles con una rejilla determinada depende de la separación de la rejilla, siendo visibles más espectros con rejillas más gruesas. La cara reglada de la rejilla debe apuntar siempre en dirección contraria a la luz incidente para evitar errores debidos a cambios de dirección por refracción en el vidrio. El diagrama muestra una franja blanca central con tres espectros a cada lado dando un total de siete imágenes.
1. Calcule la longitud de onda de la luz monocromática en la que se difracta la imagen de segundo orden a través de un ángulo de 25o utilizando una rejilla de difracción con 300 líneas por milímetro.
Espacio de la rejilla (e) = 10-3/300 m = 3.3×10-6 m
Longitud de onda (l) = esin25/2 = /2 = 6,97×10-7 m = 697 nm
2. Calcule el número máximo de órdenes visibles con una rejilla de difracción de 500 líneas por milímetro, utilizando luz de longitud de onda 600 nm.
Ángulo máximo de difracción = 90o e = 10-3/500 = 2×10-6 m
Por tanto, m = esinq/l = 2×10-6/600×10-9 = 3,33
Por tanto, el número máximo de órdenes = 3, y se pueden ver un total de siete imágenes de la fuente (tres a cada lado de una imagen central).
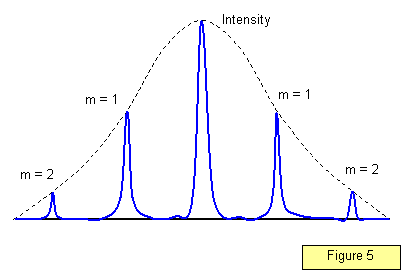
La distribución de la intensidad en el patrón de difracción para un gran número de rendijas se muestra en la figura 5. Obsérvese que los máximos se hacen mucho más nítidos; cuanto mayor es el número de rendijas por metro, mejor definidos están los máximos.
La difracción de la luz de cadmio o mercurio se utiliza para determinar la separación de dos líneas en un circuito integrado. Los siguientes resultados se obtuvieron para las imágenes difractadas de segundo orden para diferentes longitudes de onda. Utilízalos para trazar una gráfica lineal adecuada y, a partir de ahí, determinar la separación media de los hilos en el circuito.
| Longitud de onda/nm | Ángulo de difracción (o) | 468 | 28.0 | 480 | 28.7 |
| 509 | 31,0 |
| 546 | 33.0 | 577 | 35.5 | 644 | 40,0 |