¿Qué es un rango intercuartil?
El rango intercuartil es una medida de dónde está el «medio cincuenta» en un conjunto de datos. Mientras que un rango es una medida de dónde están el principio y el final en un conjunto, un rango intercuartil es una medida de dónde se encuentra la mayor parte de los valores. Por eso se prefiere sobre muchas otras medidas de dispersión cuando se informa de cosas como el rendimiento escolar o las puntuaciones del SAT.
La fórmula del rango intercuartil es el primer cuartil restado del tercer cuartil:
Contenidos (haga clic para saltar a la sección de la página):
Resolución a mano:
- Resolver la fórmula a mano (conjunto impar de números).
- ¿Qué pasa si tengo un conjunto par de números?
- Hallar un rango intercuartílico para un conjunto impar de números: Segundo método
- Rango intercuartílico de Box Plot: Cómo encontrarlo
Utilizando la tecnología:
- Rango intercuartil en Minitab
- Rango intercuartil en Excel
- Rango intercuartil en SPSS
- Rango intercuartil en el TI83
- Q1, Q3 y el IQR en el TI89
Información general:
- ¿Qué es un rango intercuartil?
- ¿Qué es la fórmula del rango intercuartílico?
- El IQR como prueba de la distribución normal
- ¿Para qué se utiliza un rango intercuartílico?
- Historia del rango intercuartílico.
Resuelve la fórmula a mano.
Mira el vídeo o lee los pasos a continuación. Si sigues teniendo dificultades, consulta los tutores de Chegg.com. Tus primeros 30 minutos son gratis!
Pasos:
- Paso 1: Pon los números en orden.
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27. - Paso 2: Encontrar la mediana.
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27. - Paso 3: Poner paréntesis alrededor de los números por encima y por debajo de la mediana.
No es necesario desde el punto de vista estadístico, pero hace que Q1 y Q3 sean más fáciles de detectar.
(1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27). - Paso 4: Encontrar Q1 y Q3
Piense en Q1 como una mediana en la mitad inferior de los datos y piense en Q3 como una mediana para la mitad superior de los datos.
(1, 2, 5, 6, 7), 9, ( 12, 15, 18, 19, 27). Q1 = 5 y Q3 = 18. - Paso 5: Resta Q1 de Q3 para encontrar el rango intercuartil.
18 – 5 = 13. - Paso 1: Poner los números en orden.
3, 5, 7, 8, 9, 11, 15, 16, 20, 21. - Paso 2: Hacer una marca en el centro de los datos:
3, 5, 7, 8, 9, | 11, 15, 16, 20, 21. - Paso 3: Poner paréntesis alrededor de los números por encima y por debajo de la marca que has hecho en el paso 2 hace que Q1 y Q3 sean más fáciles de ver.
(3, 5, 7, 8, 9), | (11, 15, 16, 20, 21). - Paso 4: Encuentra Q1 y Q3
Q1 es la mediana (el medio) de la mitad inferior de los datos, y Q3 es la mediana (el medio) de la mitad superior de los datos.
(3, 5, 7, 8, 9), | (11, 15, 16, 20, 21). Q1 = 7 y Q3 = 16. - Paso 5: Reste Q1 de Q3.
16 – 7 = 9.
Este es su IQR. - Paso 1: Encuentre Q1.Q1 está representado por el borde izquierdo de la «caja» (en el punto donde se detiene el bigote).
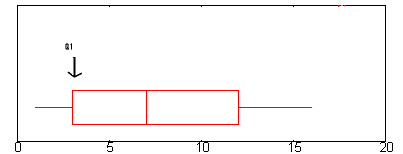
En el gráfico anterior, Q1 está aproximadamente en 2,6. (Una explicación completa de Q1 está aquí: El resumen de los cinco números.)
- Paso 2: Encontrar Q3.
Q3 está representado en un boxplot por el borde derecho de la «caja».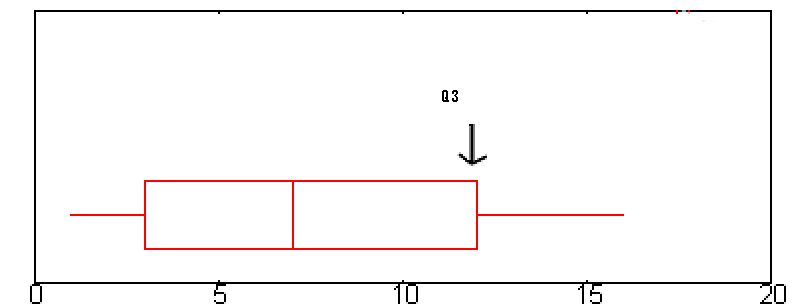
Q3 es aproximadamente 12 en este gráfico. - Paso 3: Reste el número que encontró en el paso 1 del número que encontró en el paso 3.
Esto le dará el rango intercuartil. 12 – 2,6 = 9,4. - Utilice las teclas de flecha para situar el cursor al principio del
texto que desea resaltar. - Utilizando el teclado TI, mantenga pulsada la tecla Shift y, a continuación, utilice las teclas de flecha para resaltar el texto.
- Suelte la tecla Shift y la tecla de flecha.
- Debería aparecer el menú de copiar y pegar, que le permitirá copiar y pegar los datos. Tendría que hacer esto dos veces (volviendo a la pantalla de INICIO cada vez), así que es mucho más rápido simplemente escribir los números.
Paso 7:Reste Q1 de Q3 para encontrar el IQR (strong>624 pies para este conjunto de números).
¡Eso es todo!
Volver al principioCómo encontrar Q1, Q3 y el rango intercuartílico TI 89
Mira el vídeo o lee los pasos siguientes:
Por favor, acepta las estadísticas, las cookies de marketing para ver este vídeo.Problema de ejemplo: Encuentra Q1, Q3 y el IQR para la siguiente lista de números: 1, 9, 2, 3, 7, 8, 9, 2.
Paso 1: Pulse APPS. Desplácese hasta Stats/List Editor (utilice las teclas de flecha del teclado para desplazarse). Pulse ENTER. Si no tiene el editor de estadísticas/listas puede descargarlo aquí.
Paso 2: Borre los datos del editor de listas: pulse F1 8.
Paso 3: Pulse ALPHA 9 ALPHA 1 ENTER. Esto nombra a su lista «IQ»
Paso 4: Introduzca sus números, uno a la vez. Siga cada entrada pulsando la tecla ENTER. Para nuestro grupo de números, introduzca
1,9,2,3,7,8,9,2Paso 5: Presione F4, luego ENTER (para la pantalla de estadísticas de 1 var).
Paso 6: Dígale a la calculadora que quiere estadísticas para la lista llamada «IQ» introduciendo ALPHA 9 ALPHA 1 en la casilla «Lista:». La calculadora debería poner automáticamente el cursor ahí por ti. Pulsa ENTER dos veces.
Paso 7:Lee los resultados. Q1 aparece como Q1X (en nuestro ejemplo, Q1X=2). Q3 aparece como Q3X (Q3X=8,5). Para encontrar el IQR, reste Q1 de Q3 en la pantalla de inicio. El IQR es 8,5-2=6,5.
¡Eso es todo!
Volver al principio
¿Qué es la fórmula del rango intercuartil?
La fórmula del IQR es:
IQR = Q3 – Q1Donde Q3 es el cuartil superior y Q1 es el cuartil inferior.
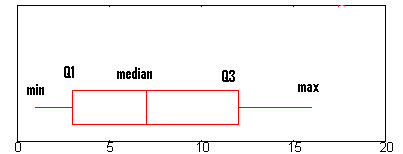
IQR como prueba de la distribución normal
Usa la fórmula del rango intercuartil con la media y la desviación estándar para probar si una población tiene o no una distribución normal. La fórmula para determinar si una población se distribuye normalmente o no son:
Q1 – (σ z1) + X
Q3 – (σ z3) + X
Donde Q1 es el primer cuartil, Q3 es el tercer cuartil, σ es la desviación estándar, z es la puntuación estándar («puntuación z») y X es la media. Para saber si una población está distribuida normalmente, resuelve ambas ecuaciones y luego compara los resultados. Si hay una diferencia significativa entre los resultados y el primer o tercer cuartil, entonces la población no está distribuida normalmente.Volver al principio
¿Para qué se utiliza el rango intercuartílico?
El IQR se utiliza para medir la dispersión de los puntos de datos de un conjunto con respecto a la media del mismo. Cuanto más alto sea el IQR, más separados estarán los puntos de datos; por el contrario, cuanto más pequeño sea el IQR, más agrupados estarán los puntos de datos alrededor de la media. El rango IQR es una de las muchas medidas utilizadas para medir la dispersión de los puntos de datos en un conjunto de datos. Se utiliza mejor con otras medidas como la mediana y el rango total para construir una imagen completa de la tendencia de un conjunto de datos a agruparse alrededor de su media.
Volver al principio¿De dónde viene el término Rango Intercuartil?
¿Quién inventó el término «Rango Intercuartil? Para averiguarlo, tenemos que remontarnos al siglo XIX.
Historia
El médico británico Sir Donald MacAlister utilizó los términos cuartil inferior y cuartil superior en la publicación de 1879, Law of the Geometric Mean. Proc. R. Soc. XXIX, p. 374: «Como estas dos medidas, con la media, dividen la curva de la facilidad en cuatro partes iguales, propongo llamarlas «cuartil superior» y «cuartil inferior» respectivamente.»

Aunque era médico de profesión, estaba dotado para las matemáticas y obtuvo la máxima puntuación en los exámenes finales de matemáticas de la Universidad de Cambridge en 1877. Hablaba diecinueve idiomas, entre ellos el inglés, el checo y el sueco.El artículo de Macalister, la Ley de la Media Geométrica fue en realidad una respuesta a una pregunta planteada por Francis Galton (inventor del tablero de Galton). Sin embargo, no fue hasta 1882 cuando Galton («Informe del Comité Antropométrico») utilizó los valores del cuartil superior y del cuartil inferior y el término «rango intercuartil» -definido como el doble del error probable. Galton no era sólo un estadístico, sino también un antropólogo, geógrafo, protogenético y psicometrista que produjo más de 340 libros. También acuñó los términos estadísticos «correlación» y «regresión a la media».
Gonick, L. y Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, pp. 20-21, 1993.
CITE THIS AS:
Stephanie Glen. «Interquartile Range (IQR): What it is and How to Find it» De StatisticsHowTo.com: ¡Estadística elemental para el resto de nosotros! https://www.statisticshowto.com/probability-and-statistics/interquartile-range/——————————————————————————
¿Necesitas ayuda con los deberes o con un examen? Con Chegg Study, puedes obtener soluciones paso a paso a tus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!
¿Te gusta la explicación? Echa un vistazo al Manual de Estadística Prácticamente Tramposa, que tiene cientos de explicaciones más paso a paso, ¡como ésta!
¿Qué pasa si tengo un conjunto par de números?
Pregunta de ejemplo: Encuentra el IQR para el siguiente conjunto de datos: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
Volver al principio
Hallar un rango intercuartílico para un conjunto de números impares: Método alternativo
Como ya sabrá, nada está «grabado en piedra» en estadística: cuando algunos estadísticos encuentran un rango intercuartil para un conjunto de números impares, incluyen la mediana en ambos cuartiles. Por ejemplo, en el siguiente conjunto de números 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27 algunos estadísticos lo dividirían en dos mitades, incluyendo la mediana (9) en ambas mitades:
(1, 2, 5, 6, 7, 9), (9, 12, 15, 18, 19, 27)
Esto lleva a dos mitades con un conjunto de números pares, por lo que se pueden seguir los pasos anteriores para encontrar el IQR.
Volver al principio
Rango intercuartílico de las gráficas de caja: Cómo encontrarlo
Mira el vídeo o lee los pasos que se indican a continuación:
Rango intercuartílico de Box Plot: Cómo encontrarlo
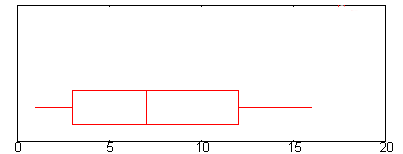

Pregunta de ejemplo: Encuentre el rango intercuartil para el gráfico de caja anterior.
¡Eso es todo!
Volver al principio
Rango intercuartil en Minitab
Siga leyendo para ver las instrucciones paso a paso, o vea la versión en vídeo a continuación.
Rango Intercuartil en Minitab: Pasos
Pregunta de ejemplo: Encuentre un rango intercuartil en Minitab para el promedio de calificaciones (GPA) en el siguiente conjunto de datos:
Promedio de calificaciones (GPA): 1(3,2), 1(3,1), 2(3,5), 2(2,0), 3(1.9), 3(4.0), 3(3.9), 4(3.8), 4(2.9), 5(3.9), 5(3.2), 5(3.3), 6(3.4), 6(2.6), 6(2.5), 7(2.0), 7(1.5), 8(4.0), 8(2.0).
Paso 1: Escriba sus datos en una hoja de trabajo de Minitab. Introduzca sus datos en una o dos columnas.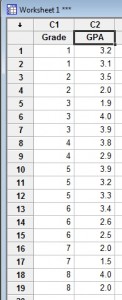
Paso 2: Haga clic en «Stat», luego haga clic en «Basic Statistics», luego haga clic en «Display Descriptive Statistics» para abrir el menú Descriptive Statistics.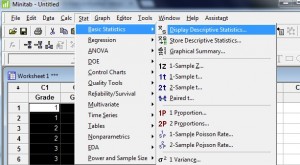
Paso 3: Haga clic en el nombre de una variable en la ventana de la izquierda y luego haga clic en el botón «Seleccionar» para transferir el nombre de la variable a la ventana de la derecha.
Paso 4: Haga clic en el botón «Estadísticas».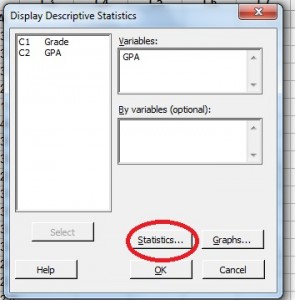
Paso 5: Marque «Rango intercuartil.»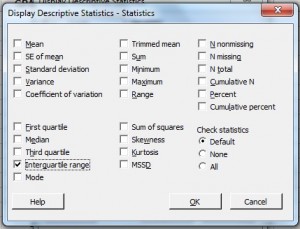 .
.
Paso 6: Haga clic en el botón «Aceptar» (se abrirá una nueva ventana con el resultado). El IQR para el GPA en este conjunto de datos en particular es 1.8.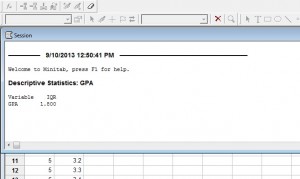
¡Eso es todo!
Consejo: Si no ves que las estadísticas descriptivas se muestran en una ventana, haz clic en «Ventana» en la barra de herramientas y luego en «Mosaico». Haga clic en la ventana Sesión (aquí es donde aparecen las estadísticas descriptivas) y luego desplácese hacia arriba para ver sus resultados.
Volver al principio
Cómo encontrar un rango intercuartil Excel 2007
Vea el vídeo o lea los pasos siguientes para encontrar un rango intercuartil en Excel 2007:
Pasos:
Paso 1: Introduzca sus datos en una sola columna de Excel en una hoja de cálculo. Por ejemplo, escriba sus datos en las celdas A2 a A10. No deje ningún hueco en sus datos.
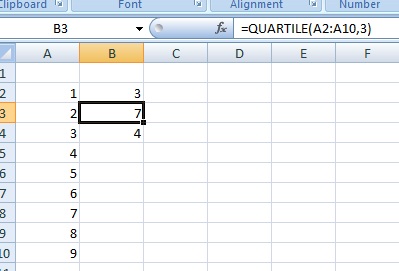
Paso 2: Haga clic en una celda en blanco (por ejemplo, haga clic en la celda B2) y luego escriba =QUARTILE(A2:A10,1). Tendrá que sustituir A2:A10 por los valores reales de su conjunto de datos. Por ejemplo, si escribiste tus datos en B2 a B50, la ecuación es =CUÁRTILA(B2:B50,1). El «1» en esta fórmula de Excel(A2:A10,1) representa el primer cuartil (es decir, el punto situado en el 25% del conjunto de datos).
Paso 3: Haga clic en una segunda celda en blanco (por ejemplo, haga clic en la celda B3) y, a continuación, escriba =CUÁRTILA(A2:A10,3). Sustituya A2:A10 por los valores reales de su conjunto de datos. El «3» en esta fórmula de Excel (A2:A10,3) representa el tercer cuartil (es decir, el punto que se encuentra en el 75% del conjunto de datos).
Paso 4: Haga clic en una tercera celda en blanco (por ejemplo, haga clic en la celda B4) y luego escriba =B3-B2. Si sus funciones de cuartil de los pasos 2 y 3 están en lugares diferentes, cambie las referencias de las celdas.
Paso 5: Pulse la tecla «Intro». Excel devolverá el IQR en la celda en la que hizo clic en el Paso 4
¡Eso es todo!
Volver al principio
Cómo encontrar un rango intercuartil en SPSS
Como la mayoría de la tecnología, SPSS tiene varias formas en las que puede calcular el IQR. Sin embargo, si hace clic en la forma más intuitiva que esperaría encontrar («Estadísticas Descriptivas > Frecuencias»), la sorpresa es que no listará el IQR (aunque sí el primer, segundo y tercer cuartil). Podría seguir este camino y luego restar el tercer cuartil del primero para obtener el IQR. Sin embargo, la forma más fácil de encontrar el rango intercuartil en SPSS es utilizando el comando «Explorar». Si ya ha introducido los datos en su hoja de trabajo, salte al Paso 3.
Vea el vídeo o lea los pasos que se indican a continuación:
Pasos
Paso 1: Abra un nuevo archivo de datos en SPSS. Haga clic en «Archivo», pase el ratón por encima de «Nuevo» y luego haga clic en «Datos».
Paso 2: Escriba sus datos en columnas en la hoja de trabajo. Puede utilizar tantas columnas como necesite, pero no deje filas en blanco ni espacios entre sus datos. Ver: Cómo introducir datos en el SPSS.
Paso 3: Haga clic en «Analizar» y luego pase el ratón por encima de «Estadísticas descriptivas». Haga clic en «Explorar» para abrir el cuadro de diálogo «Explorar».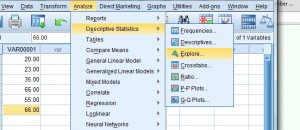
Paso 4: Haga clic en el nombre de la variable (que es sólo un nombre elegante para el encabezado de la columna), luego haga clic en la flecha superior para mover la variable en el cuadro «Lista dependiente».
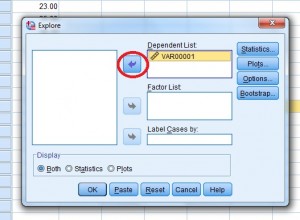
El cuadro de diálogo «Explorar» variables.
Paso 5: Haga clic en «Aceptar». El rango intercuartil aparece en el cuadro Descriptivos.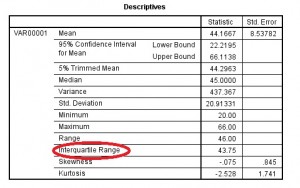
Consejo: Este ejemplo sólo tiene una lista escrita en la hoja de datos, pero puede tener varias para elegir dependiendo de cómo haya introducido sus datos. Asegúrese de seleccionar la variable correcta (nombres de columnas) antes de continuar. Si desea nombres de variables más memorables, cambie el título de la columna haciendo clic en el botón «vista de la variable» situado en la parte inferior izquierda de la hoja de cálculo. Escriba el nuevo nombre de la variable y vuelva a la vista de datos haciendo clic en el botón «vista de datos».
Volver al principio
¿Qué es un rango intercuartílico?
Imagine todos los datos de un conjunto como puntos en una recta numérica. Por ejemplo, si tiene 3, 7 y 28 en su conjunto de datos, imagínelos como puntos en una línea numérica centrada en el 0 pero que se extiende infinitamente por debajo del cero y por encima del cero. Una vez trazados en esa recta numérica, el punto de datos más pequeño y el punto de datos más grande del conjunto de datos crean los límites (es decir, un límite inferior y un límite superior) de un intervalo de espacio en la recta numérica que contiene todos los puntos de datos del conjunto. El rango intercuartil (IQR) es la longitud del 50% medio de ese intervalo de espacio.
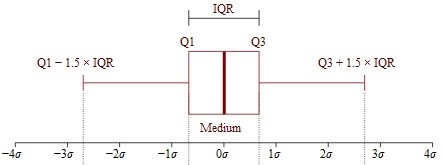
El rango intercuartil es el 50% medio de un conjunto de datos. Box and whiskers image by Jhguch at es.wikipedia
Si quieres saber que es el IQR en términos formales, el IQR se calcula como: La diferencia entre el tercer cuartil o superior y el primer cuartil o inferior. El cuartil es un término utilizado para describir la forma de dividir el conjunto de datos en cuatro porciones iguales (piense en un cuarto).
Ejemplo de IQR
Si tienes un conjunto que contiene los puntos de datos 1, 3, 5, 7, 8, 10, 11 y 13, el primer cuartil es 4, el segundo cuartil es 7,5 y el tercer cuartil es 10,5. Dibuja estos puntos en una recta numérica y verás que esos tres números dividen la recta numérica en cuartos del 1 al 13. Por tanto, el IQR de ese conjunto de datos es 6,5, calculado como 10,5 menos 4. Los cuartiles primero y tercero también se denominan a veces percentiles 25 y 75 porque esas son las cifras equivalentes cuando el conjunto de datos se divide en porcentajes en lugar de en trimestres.
Volver al principio
Rango intercuartílico con la TI83
Mira el vídeo o lee los pasos que se indican a continuación:
Aunque puedes utilizar la ingeniosa calculadora de rango intercuartílico en línea de este sitio web, puede que no sea una opción en un examen o prueba. La mayoría de los instructores permiten el uso de una TI-83 en los exámenes, e incluso es una de las pocas calculadoras permitidas en el examen de Estadística AP. Encontrar el rango intercuartil de la TI 83 no implica nada más que introducir su lista de datos y pulsar un par de botones.
Problema de ejemplo: Encuentre el rango intercuartil de la TI 83 para las alturas de los 10 edificios más importantes del mundo (en 2009). Las alturas, (en pies) son: 2717, 2063, 2001, 1815, 1516, 1503, 1482, 1377, 1312, 1272.
Pasos
Paso 1: Introduzca los datos anteriores en una lista de la calculadora TI 83. Pulse el botón STAT y luego pulse ENTER. Introduzca el primer número (2717), y luego pulse ENTER. Continúe introduciendo números, pulsando ENTER después de cada entrada.
Paso 2: Pulse el botón STAT.
Paso 3: Pulse el botón de flecha derecha (las teclas de flecha se encuentran en la parte superior derecha del teclado) para seleccionar «Calc.»
Paso 4: Pulse ENTER para resaltar «1-Var Stats.»
Paso 5: Pulse ENTER de nuevo para que aparezca una lista de estadísticas.
Paso 6:Desplácese por la lista con las teclas de flecha para encontrar Q1 y Q3. Escriba esos números. Podría copiar y pegar los números, pero desgraciadamente, Texas Instruments no se lo pone fácil: