El modelo de espacio de estados del sistema lineal invariante en el tiempo (LTI) puede representarse como,
$\dot{X}=AX+BU$
$Y=CX+DU$
La primera y la segunda ecuación se conocen como ecuación de estado y ecuación de salida respectivamente.
Donde,
-
X y $\dot{X}$ son el vector de estado y el vector de estado diferencial respectivamente.
-
U e Y son el vector de entrada y el vector de salida respectivamente.
-
A es la matriz del sistema.
-
B y C son las matrices de entrada y de salida.
-
D es la matriz feed-forward.
Conceptos básicos del modelo de espacio de estados
La siguiente terminología básica involucrada en este capítulo.
Estado
Es un grupo de variables, que resume la historia del sistema con el fin de predecir los valores futuros (salidas).
Variable de estado
El número de variables de estado requeridas es igual al número de elementos de almacenamiento presentes en el sistema.
Ejemplos – la corriente que fluye a través del inductor, el voltaje a través del condensador
Vector de estado
Es un vector, que contiene las variables de estado como elementos.
En los capítulos anteriores, hemos discutido dos modelos matemáticos de los sistemas de control. Estos son el modelo de ecuaciones diferenciales y el modelo de funciones de transferencia. El modelo de espacio de estado puede ser obtenido a partir de cualquiera de estos dos modelos matemáticos. Ahora vamos a discutir estos dos métodos uno por uno.
Modelo de espacio de estado a partir de la ecuación diferencial
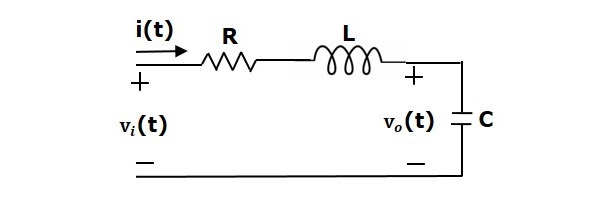
Hay dos elementos de almacenamiento (inductor y condensador) en este circuito. Por lo tanto, el número de las variables de estado es igual a dos y estas variables de estado son la corriente que fluye a través del inductor, $i(t)$ y la tensión a través del condensador, $v_c(t)$.
Del circuito, la tensión de salida, $v_0(t)$ es igual a la tensión a través del condensador, $v_c(t)$.
$v_0(t)=v_c(t)$
Aplica el KVL alrededor de la espira.
$v_i(t)=Ri(t)+L\frac{text{d}i(t)}{text{d}t}+v_c(t)$
$ Flecha derecha \frac{text{d}i(t)}=-\frac{Ri(t)}{L}-\frac{v_c(t)}{L}+\frac{v_i(t)}{L}$
La tensión en el condensador es –
$v_c(t)=\frac{1}{C} \int i(t) dt$
Diferencie la ecuación anterior con respecto al tiempo.
$frac{{text{d}v_c(t)}{text{d}t}={frac{i(t)}{C}$
Vector de estado, $X=\begin{bmatrix}i(t) \v_c(t) \bmatrix}$
Vector de estado diferencial, $\dot{X}=\begin{bmatrix}\frac{text{d}i(t)}{text{d}t} \\\frac{\text{d}v_c(t)}{\text{d}t} \nd{bmatrix}$
Podemos ordenar las ecuaciones diferenciales y la ecuación de salida en la forma estándar del modelo de espacio de estados como,
$Y={begin{bmatrix}0 & 1 \end{bmatrix}{begin{bmatrix}i(t) \v_c(t) \end{bmatrix}$
Donde,
Modelo de espacio de estados a partir de la función de transferencia
Considera los dos tipos de funciones de transferencia en función del tipo de términos presentes en el numerador.
- Función de transferencia que tiene un término constante en el numerador.
- Función de transferencia que tiene una función polinómica de ‘s’ en el numerador.
Función de transferencia que tiene un término constante en el Numerador
Considere la siguiente función de transferencia de un sistema
$\frac{Y(s)}{U(s)}=\frac{b_0}{s^n+a_{n-1}s^{n-1}+…+a_1s+a_0}$
Regular, la ecuación anterior como
$(s^n+a_{n-1}s^{n-1}+…+a_0)Y(s)=b_0 U(s)$
Aplicar la transformada inversa de Laplace en ambos lados.
$\frac{\text{d}^ny(t)}{\text{d}t^n}+a_{n-1}\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}+…+a_1\frac{text{d}y(t)}{text{d}t}+a_0y(t)=b_0 u(t)$
Dejemos
$y(t)=x_1$
$\frac{\text{d}y(t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2y(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^ny(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then,
$\dot{x}_n+a_{n-1}x_n+…+a_1x_2+a_0x_1=b_0 u$
A partir de la ecuación anterior, podemos escribir la siguiente ecuación de estado.
$\dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+b_0 u$
La ecuación de salida es –
$y(t)=y=x_1$
El modelo del espacio de estados es –
${dot{X}={bmatrix}{dot{x}_1}{dot{x}_2}{dot{x}}1} \\N – fin{bmatrix}$
$Y={begin{bmatrix}1 && \dotso && 0 \end{bmatrix}\begin{bmatrix}x_1 \x_2 \\vdots \x_{n-1} \x_n \N – fin{bmatrix}$
Aquí, $D=\\NIzquierda .$
Ejemplo
Encuentra el modelo de espacio de estados para el sistema que tiene función de transferencia.
$frac{Y(s)}{U(s)}=\frac{1}{s^2+s+1}$
Reordenar, la ecuación anterior como,
$(s^2+s+1)Y(s)=U(s)$
Aplicar la transformada inversa de Laplace en ambos lados.
$frac{{text{d}^2y(t)}{text{d}t^2}+frac{text{d}y(t)}{text{d}t}+y(t)=u(t)$
Dejemos
$y(t)=x_1$
$frac{text{d}y(t)}{text{d}t}=x_2={dot{x}_1$
y $u(t)=u$
Entonces, la ecuación de estado es
$\dot{x}_2=-x_1-x_2+u$
La ecuación de salida es
$y(t)=y=x_1$
El modelo del espacio de estado es
$Y=\begin{bmatrix}1 & 0 \end{bmatrix}\begin{bmatrix}x_1 \x_2 \end{bmatrix}$
Función de transferencia que tiene una función polinómica de ‘s’ en el numerador
Consideremos la siguiente función de transferencia de un sistema
$frac{Y(s)}{U(s)}=\frac{b_n s^n+b_{n-1}s^{n-1}+….+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$
$ Flecha derecha \frac{Y(s)}{U(s)}=left( \frac{1}s^n+a_{n-1}+…+a_1 s+a_0} \N-derecha )(b_n s^n+b_{n-1}s^{n-1}+…+b_1s+b_0)$
La ecuación anterior está en forma de producto de funciones de transferencia de dos bloques, que están en cascada.
$frac{Y(s)}{U(s)}=left(\frac{V(s)}{U(s)} \right ) \left(\frac{Y(s)}{V(s)} \a derecha )$
Aquí,
$frac{V(s)}{U(s)}=\frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$
Recolocar, la ecuación anterior como
$(s^n+a_{n-1}s^{n-1}+…+a_0)V(s)=U(s)$
Aplique la transformada inversa de Laplace en ambos lados.
$frac{text{d}^nv(t)}{text{d}t^n}+a_{n-1}{frac{text{d}^{n-1}v(t)}{text{d}t^{n-1}+…+a_1 \frac{text{d}v(t)}{text{d}t}+a_0v(t)=u(t)$
Dejemos
$v(t)=x_1$
$\frac{\text{d}v((t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2v(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^nv(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then, la ecuación de estado es
$\dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+u$
Consider,
$\frac{Y(s)}{V(s)}=b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0$
Reordenar, la ecuación anterior como
$Y(s)=(b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0)V(s)$
Aplicar la transformada inversa de Laplace en ambos lados.
$y(t)=b_n\frac{\text{d}^nv(t)}{\text{d}t^n}+b_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+…+b_1\frac{text{d}v(t)}{text{d}t}+b_0v(t)$
Sustituyendo las variables de estado y $y(t)=y$ en la ecuación anterior, obtendremos la ecuación de salida como,
$y=b_n{dot{x}_n+b_{n-1}x_n+…+b_1x_2+b_0x_1$
Sustituir, $\dot{x}_n$ valor en la ecuación anterior.
$y=b_n(-a_0x_1-a_1x_2-…-a_{n-1}x_n+u)+b_{n-1}x_n+…+b_1x_2+b_0x_1$
$y=(b_0-b_na_0)x_1+(b_1-b_na_1)x_2+…+(b_{n-1}-b_na_{n-1})x_n+b_n u$
El modelo del espacio de estados es
$\dot{X}=\begin{bmatrix}{dot{x}_1 \\\dot{x}_2 \\vdots \dot{x}_{n-1} \\\N-fin{bmatrix}$
$Y={bmatrix}x_1 \\N-\N-\N-\N-\N-\N-\N-\N-fin{bmatrix}$
Si $b_n = 0$, entonces,
$Y=\begin{bmatrix}x_1 \\x_2 \\\\vdots \x_{n-1} \x_n \nd{bmatrix}$