El método de los multiplicadores de Lagrange es el caballo de batalla de los economistas para resolver problemas de optimización. La técnica es una pieza central de la teoría económica, pero, por desgracia, suele enseñarse mal.
La mayoría de los libros de texto se centran en la elaboración mecánica de fórmulas, dejando a los estudiantes desconcertados sobre por qué funciona realmente, para empezar. En este post, explicaré una forma sencilla de ver por qué los multiplicadores de Lagrange realmente hacen lo que hacen, es decir, resolver problemas de optimización con restricciones mediante el uso de una función lagrangiana semimisteriosa.
Algunos antecedentes
Antes de que puedas ver por qué el método funciona, tienes que saber algo sobre gradientes. Para funciones de una variable hay – normalmente – una primera derivada. Para funciones de n variables, hay n primeras derivadas. Un gradiente es sólo un vector que recoge todas las primeras derivadas parciales de la función en un solo lugar.
Cada elemento del gradiente es una de las primeras derivadas parciales de la función. Una forma fácil de pensar en un gradiente es que si elegimos un punto en alguna función, nos da la «dirección» hacia la que se dirige la función. Si nuestra función está etiquetada
la notación para el gradiente de f es
Lo más importante que hay que saber sobre los gradientes es que siempre apuntan en la dirección de la mayor pendiente de una función en un punto determinado. Para ayudar a ilustrar esto, echa un vistazo al dibujo de abajo. Ilustra cómo funcionan los gradientes para una función de dos variables de x1 y x2.
La función f en el dibujo forma una colina. Hacia la cima he dibujado dos regiones en las que mantenemos la altura de f constante en algún nivel a. Estas se llaman curvas de nivel de f, y están marcadas como f = a1, y f = a2.
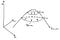
Imagínate de pie en una de esas curvas de nivel. Piensa en una ruta de senderismo en la ladera de una montaña. De pie en el sendero, ¿en qué dirección es más empinada la montaña? Está claro que la dirección más empinada es la recta hacia arriba de la colina, perpendicular al sendero. En el dibujo, estos caminos de subida más pronunciada están marcados con flechas. Estas son las pendientes
en varios puntos de las curvas de nivel. Al igual que la subida más pronunciada es siempre perpendicular a nuestro camino, las pendientes de f son siempre perpendiculares a sus curvas de nivel.
Esa es la idea clave aquí: las curvas de nivel son donde
Y
Cómo funciona el método
Para ver cómo funcionan los multiplicadores de Lagrange, echa un vistazo al dibujo de abajo. He redibujado la función f de arriba, junto con una restricción g = c. En el dibujo, la restricción es un plano que corta nuestra ladera. También he dibujado un par de curvas de nivel de f.

Nuestro objetivo aquí es subir tan alto en la colina como podamos, dado que no podemos movernos más alto que donde la restricción g = c corta la colina.
En el dibujo, la frontera donde la restricción corta la función está marcada con una línea gruesa. A lo largo de esa línea están los puntos más altos que podemos alcanzar sin pisar nuestra restricción. Ese es un lugar obvio para empezar a buscar un máximo restringido.
Imagina que caminas de izquierda a derecha sobre la línea de la restricción. A medida que ganamos altura, recorremos varias curvas de nivel de f. He marcado dos en la imagen. En cada curva de nivel, imagina que compruebas su pendiente -es decir, la pendiente de una recta tangente a ella- y la comparas con la pendiente de la restricción donde estamos parados.
Si nuestra pendiente es mayor que la curva de nivel, podemos llegar a un punto más alto de la colina si seguimos avanzando hacia la derecha. Si nuestra pendiente es menor que la curva de nivel -digamos, hacia la derecha donde nuestra línea de restricción está disminuyendo- tenemos que retroceder hacia la izquierda para alcanzar un punto más alto.
Cuando alcanzamos un punto en el que la pendiente de la línea de restricción justo es igual a la pendiente de la curva de nivel, nos hemos movido lo más alto posible. Es decir, hemos alcanzado nuestro máximo restringido. Cualquier movimiento a partir de ese punto nos llevará hacia abajo. En la figura, este punto está marcado con una gran flecha que apunta hacia el pico.
En ese punto, la curva de nivel f = a2 y la restricción tienen la misma pendiente. Eso significa que son paralelas y apuntan en la misma dirección. Pero como vimos anteriormente, los gradientes son siempre perpendiculares a las curvas de nivel. Así que si estas dos curvas son paralelas, sus gradientes también deben ser paralelos.
Eso significa que los gradientes de f y g apuntan a la misma dirección, y difieren como mucho en un escalar. Llamemos a ese escalar «lambda». Entonces tenemos,
Resolviendo para cero, obtenemos
Esta es la condición que debe cumplirse cuando hemos alcanzado el máximo de f sujeto a la restricción g = c. Ahora, si somos inteligentes podemos escribir una única ecuación que capture esta idea. Aquí es donde entra la conocida ecuación lagrangiana:
o más explícitamente,
Para ver cómo funciona esta ecuación, observemos lo que ocurre cuando seguimos el procedimiento lagrangiano habitual. Primero, encontramos las tres primeras derivadas parciales de L,
y ponerlos a cero. Es decir, necesitamos establecer el gradiente de L igual a cero. Para encontrar el gradiente de L, tomamos las tres derivadas parciales de L con respecto a x1, x2 y lambda. Luego colocamos cada una como un elemento en un vector de 3 x 1. Eso nos da lo siguiente:
Recuerda que tenemos dos «reglas» que seguir aquí. Primero, los gradientes de f y g deben apuntar en la misma dirección, o
Y segundo, tenemos que satisfacer nuestra restricción, o
El primer y segundo elemento del gradiente de L se encargan de que se cumpla la primera regla. Es decir, obligan
asegurando que los gradientes de f y g apuntan ambos en la misma dirección. El tercer elemento del gradiente de L es simplemente un truco para asegurar que g = c, que es nuestra restricción. En la función lagrangiana, cuando tomamos la derivada parcial con respecto a lambda, simplemente nos devuelve nuestra ecuación de restricción original.
En este punto, tenemos tres ecuaciones en tres incógnitas. Así que podemos resolver esto para los valores óptimos de x1 y x2 que maximizan f sujeto a nuestra restricción. Y ya hemos terminado.
Así que la conclusión es que los multiplicadores de Lagrange son realmente un algoritmo que encuentra donde el gradiente de una función apunta en la misma dirección que los gradientes de sus restricciones, mientras que también satisface esas restricciones.
Como con la mayoría de las áreas de las matemáticas, una vez que ves el fondo de las cosas – en este caso, que la optimización es realmente sólo la escalada de colinas, que todo el mundo entiende – las cosas son mucho más simples que la mayoría de los economistas hacen que sean.