Ritorna all’indice delle lezioni | Fai le lezioni in ordine | Stampa la pagina
Fattoriali
I fattoriali sono cose molto semplici. Sono solo prodotti, indicati da un punto esclamativo. Per esempio, “quattro fattoriali” è scritto come “4!” e significa 1×2×3×4 = 24. In generale, n! (“enn factorial”) significa il prodotto di tutti i numeri interi da 1 a n; cioè, n! = 1×2×3×…×n.
(Per varie ragioni, 0! è definito uguale a 1, non 0. Memorizzate questo ora: 0! = 1.)
- Valuta 6!
1×2×3×4×5×6 = 720
Molte (la maggior parte?) calcolatrici possono valutare i fattoriali per voi. Per esempio, il comando fattoriale è disponibile nel menu “probabilità” di una delle mie calcolatrici:

Cercare un pulsante ” ! “
- Semplificare 12! Copyright © Elizabeth Stapel 2004-2011 Tutti i diritti riservati
12! = 1×2×3×4×… Oh, al diavolo questo. Dov’è la mia calcolatrice…?

12! = 479001600
Avviso
Quando inizierai a fare combinazioni, permutazioni e probabilità, dovrai semplificare espressioni che hanno fattoriali nei numeratori e nei denominatori. Per esempio:
- Semplifica quanto segue:
![]()
Posso fare questo nella mia calcolatrice:

Posso anche lavorare dalla definizione di un fattoriale:
![]()
In entrambi i casi, 6! ÷ 4! = 30
Nota come sono stato in grado di cancellare un sacco di numeri nel problema precedente. Questo è dovuto a come sono definiti i fattoriali, e questa proprietà può semplificare molto il tuo lavoro.
- Semplifica quanto segue:
![]()
Subito, posso cancellare i fattori da 1 a 14 che saranno comuni a 17! e 14!. Poi posso semplificare ciò che rimane per ottenere:
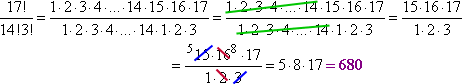
Nota come ho accorciato quello che dovevo scrivere lasciando uno spazio (l'”ellissi”, o triplo punto) nel mezzo. Questo processo di interruzione e cancellazione diventerà utile in seguito (come nel calcolo, dove userete questa tecnica molto spesso), specialmente quando avrete a che fare con espressioni che la vostra calcolatrice non può gestire. Per esempio:
- Semplificate il seguente:
![]()
La mia calcolatrice non può valutare questo per me, poiché ho a che fare con variabili piuttosto che con numeri. Dovrò semplificare questo a mano. Per fare questo, scriverò i fattoriali, usando abbastanza fattori per avere cose che possono annullarsi. Ripensando ai problemi di parole “numerici”, i numeri interi consecutivi sono distanti un’unità, quindi i fattori nel prodotto (n + 2)! sono della forma:
1×2×3×4×…×(n – 1)×(n)×(n + 1)×(n + 2)
Scendendo la lista dei fattori fino a “n – 1”, ho creato una lista di fattori che possono annullarsi:
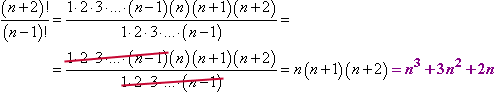
Fate attenzione al modo in cui ho gestito questa cancellazione. Ho espanso le espressioni fattoriali abbastanza da poter vedere dove potevo cancellare i fattori duplicati. Anche se non avevo idea di quale potesse essere n, potevo comunque annullare. Archiviate questa tecnica nel vostro cervello, perché anche se non ne avete bisogno ora, quasi certamente ne avrete bisogno più tardi.
Per informazioni su come trovare il numero di zeri alla fine di un fattoriale (come “Quanti zeri ci sono alla fine di 23! dopo averlo moltiplicato?”), guarda questa nota.
Top | Return to Index
|
Cita questo articolo come: |
Stapel, Elizabeth. “Fattoriali”. Purplemath. Disponibile da 2016
|