Heading

Forse non conservative e attrito

Le forze possono essere conservative o non conservative. Le forze conservative sono state discusse in Forze conservative ed energia potenziale. Una forza non conservativa è una forza per la quale il lavoro dipende dal percorso intrapreso. L’attrito è un buon esempio di forza non conservativa. Come illustrato nella Figura 1, il lavoro fatto contro l’attrito dipende dalla lunghezza del percorso tra i punti di partenza e di arrivo. A causa di questa dipendenza dal percorso, non c’è energia potenziale associata alle forze non conservative. Una caratteristica importante è che il lavoro fatto da una forza non conservativa aggiunge o toglie energia meccanica da un sistema. L’attrito, per esempio, crea energia termica che si dissipa, rimuovendo energia dal sistema. Inoltre, anche se l’energia termica viene trattenuta o catturata, non può essere completamente riconvertita in lavoro, quindi è persa o non recuperabile anche in questo senso.

Figura 1. La quantità della faccia felice cancellata dipende dal percorso fatto dalla gomma tra i punti A e B, così come il lavoro fatto contro l’attrito. Viene fatto meno lavoro e viene cancellata meno faccia per il percorso in (a) che per il percorso in (b). La forza qui è l’attrito, e la maggior parte del lavoro va in energia termica che successivamente lascia il sistema (la faccia felice più la gomma). L’energia spesa non può essere completamente recuperata.

Come le forze non conservative influenzano l’energia meccanica

L’energia meccanica può non essere conservata quando agiscono forze non conservative. Per esempio, quando un’auto viene portata a fermarsi per attrito su un terreno piano, perde energia cinetica, che viene dissipata come energia termica, riducendo la sua energia meccanica. La figura 2 confronta gli effetti delle forze conservative e non conservative. Spesso scegliamo di capire prima sistemi più semplici come quello descritto nella figura 2a prima di studiare sistemi più complicati come quello della figura 2b.

Figura 2. Confronto degli effetti delle forze conservative e non conservative sull’energia meccanica di un sistema. (a) Un sistema con solo forze conservative. Quando un sasso viene lasciato cadere su una molla, la sua energia meccanica rimane costante (trascurando la resistenza dell’aria) perché la forza nella molla è conservativa. La molla può spingere il sasso indietro alla sua altezza originale, dove ancora una volta ha solo energia potenziale dovuta alla gravità. (b) Un sistema con forze non conservative. Quando la stessa roccia viene lasciata cadere sul terreno, viene fermata da forze non conservative che dissipano la sua energia meccanica come energia termica, suono e distorsione della superficie. La roccia ha perso energia meccanica.

Come si applica il teorema lavoro-energia

Ora consideriamo quale forma assume il teorema lavoro-energia quando agiscono sia forze conservative che non conservative. Vedremo che il lavoro fatto dalle forze non conservative è uguale al cambiamento dell’energia meccanica di un sistema. Come notato in Energia cinetica e il teorema lavoro-energia, il teorema lavoro-energia afferma che il lavoro netto su un sistema è uguale al cambiamento della sua energia cinetica, o Wnet = ΔKE. Il lavoro netto è la somma del lavoro delle forze non conservative più il lavoro delle forze conservative. Cioè,

Wnet = Wnc + Wc,

così che

Wnc + Wc = ΔKE,

dove Wnc è il lavoro totale fatto da tutte le forze non conservatrici e Wc è il lavoro totale fatto da tutte le forze conservatrici.

Figura 3. Una persona spinge una cassa su per una rampa, facendo lavoro sulla cassa. Anche l’attrito e la forza gravitazionale (non mostrata) fanno lavoro sulla cassa; entrambe le forze si oppongono alla spinta della persona. Mentre la cassa viene spinta su per la rampa, guadagna energia meccanica, il che implica che il lavoro fatto dalla persona è maggiore del lavoro fatto dall’attrito.

Consideriamo la figura 3, in cui una persona spinge una cassa su per una rampa ed è contrastata dall’attrito. Come nella sezione precedente, notiamo che il lavoro fatto da una forza conservativa deriva da una perdita di energia potenziale gravitazionale, così che Wc = -ΔPE. Sostituendo questa equazione nella precedente e risolvendo per Wnc si ottiene

Wnc = ΔKE + ΔPE.

Questa equazione significa che l’energia meccanica totale (KE + PE) cambia esattamente della quantità di lavoro fatto dalle forze non conservative. Nella figura 3, questo è il lavoro fatto dalla persona meno il lavoro fatto dall’attrito. Quindi, anche se l’energia non si conserva per il sistema di interesse (come la cassa), sappiamo che è stata fatta una quantità uguale di lavoro per causare il cambiamento dell’energia meccanica totale.

Riorganizziamo Wnc = ΔKE + ΔPE per ottenere

KEi + PEi + Wnc = KEf + PEf.

Questo significa che la quantità di lavoro fatto da forze non conservative si aggiunge all’energia meccanica di un sistema. Se Wnc è positivo, allora l’energia meccanica aumenta, come quando la persona spinge la cassa su per la rampa nella figura 3. Se Wnc è negativo, allora l’energia meccanica è diminuita, come quando la roccia colpisce il terreno nella Figura 2b. Se Wnc è zero, allora l’energia meccanica si conserva e le forze non conservative sono bilanciate. Per esempio, quando si spinge un tosaerba a velocità costante su un terreno piano, il lavoro fatto viene rimosso dal lavoro di attrito, e il tosaerba ha un’energia costante.

Applicare la conservazione dell’energia con forze non conservative

Quando non si verifica alcun cambiamento nell’energia potenziale, applicare KEi + PEi + Wnc = KEf + PEf equivale ad applicare il teorema lavoro-energia impostando il cambiamento nell’energia cinetica per essere uguale al lavoro netto fatto sul sistema, che nel caso più generale include sia forze conservative che non conservative. Ma quando si cerca invece di trovare un cambiamento nell’energia meccanica totale in situazioni che coinvolgono cambiamenti sia nell’energia potenziale che in quella cinetica, l’equazione precedente KE i + PEi + Wnc = KEf + PEf dice che si può iniziare trovando il cambiamento nell’energia meccanica che sarebbe risultato dalle sole forze conservative, incluse le variazioni di energia potenziale, e aggiungere ad esso il lavoro fatto, con il segno appropriato, da qualsiasi forza non conservativa coinvolta.

Esempio 1. Calcolo della distanza percorsa: Quanto lontano scivola un giocatore di baseball

Considera la situazione mostrata nella Figura 4, dove un giocatore di baseball scivola fino a fermarsi su un terreno piano. Utilizzando le considerazioni sull’energia, calcolare la distanza che il giocatore di baseball di 65,0 kg scivola, dato che la sua velocità iniziale è di 6,00 m/s e la forza di attrito contro di lui è costante 450 N.

Figura 4. Il giocatore di baseball scivola fino a fermarsi in una distanza d. Nel processo, l’attrito rimuove l’energia cinetica del giocatore facendo una quantità di lavoro pari all’energia cinetica iniziale.

Strategia

L’attrito ferma il giocatore convertendo la sua energia cinetica in altre forme, compresa quella termica. In termini di teorema lavoro-energia, il lavoro fatto dall’attrito, che è negativo, si aggiunge all’energia cinetica iniziale per ridurla a zero. Il lavoro fatto dall’attrito è negativo, perché f è nella direzione opposta al moto (cioè, θ = 180º, e quindi cos θ = -1). Quindi Wnc = -fd. L’equazione si semplifica in

frac{1}{2}{mv_{\testo{i}}}^2-fd=0\\}

o

fd=\frac{1}{2}{mv_{\testo{i}}^2\.

Questa equazione può ora essere risolta per la distanza d.

Soluzione

Solvendo l’equazione precedente per d e sostituendo i valori noti si ottiene

egin{array}{lll}d&&\frac{mv_{\text{i}}^2}{2f}\\\text{ }&&\frac{(65.0{ kg})(6,00{ m/s})^2}{(2)(450{text{ N})}{&&2.60\testo{ m}{array}\fine

Discussione

Il punto più importante di questo esempio è che la quantità di lavoro non conservativo è uguale alla variazione di energia meccanica. Per esempio, bisogna lavorare di più per fermare un camion, con la sua grande energia meccanica, che per fermare una zanzara.

Esempio 2. Calcolo della distanza percorsa: Scivolamento su una pendenza

Supponiamo che il giocatore dell’esempio 1 stia correndo su una collina con una pendenza di 5,00º verso l’alto con una superficie simile a quella dello stadio di baseball. Il giocatore scivola con la stessa velocità iniziale. Determinare quanto lontano scivola.

Figura 5. Lo stesso giocatore di baseball scivola fino a fermarsi su una pendenza di 5,00º.

Strategia

In questo caso, il lavoro fatto dalla forza d’attrito non conservativa sul giocatore riduce l’energia meccanica che ha dalla sua energia cinetica ad altezza zero, all’energia meccanica finale che ha spostandosi per la distanza d per raggiungere l’altezza h lungo la collina, con h = d sin 5,00º. Questo è espresso dall’equazione KE + PEi + Wnc = KE f + PEf.

Soluzione

Il lavoro fatto dall’attrito è di nuovo Wnc = -fd; inizialmente l’energia potenziale è PEi = mg – 0 = 0 e l’energia cinetica è \text{KE}_{\text{i}}=frac{1}{2}mv_{\text{i}}^2\; i contributi energetici finali sono KEf = 0 per l’energia cinetica e PEf = mgh = mgd sin θ per l’energia potenziale.

Sostituendo questi valori si ottiene

frac{1}{2}{mv_{\testo{i}}}^2+0+\sinistra(-fd-destra)=0+mgd\sin\the\ta\

Solvere questo per d per ottenere

begin{array}{lll}d&&\frac{\left(\frac{1}{2}\right)mv_{\text{i}}^2}{f+mg\sin\theta}\\&&\frac{(0.5)(65,0{ kg})(6,00{ m/s})^2}{450{text{ N}+(65,0{ kg})\sinistra(9,80{ m/s}^2{destra)\sin(5,00^{circa})}&&2.31\testo{ m}{array}\fine

Discussione

Come ci si poteva aspettare, il giocatore scivola per una distanza più breve scivolando in salita. Si noti che il problema avrebbe potuto essere risolto anche in termini di forze direttamente e con il teorema dell’energia di lavoro, invece di usare l’energia potenziale. Questo metodo avrebbe richiesto la combinazione dei vettori forza normale e forza di gravità, che non si annullano più a vicenda perché puntano in direzioni diverse, e l’attrito, per trovare la forza netta. Si potrebbe poi usare la forza netta e il lavoro netto per trovare la distanza d che riduce l’energia cinetica a zero. Applicando la conservazione dell’energia e usando invece l’energia potenziale, dobbiamo considerare solo l’energia potenziale gravitazionale mgh, senza combinare e risolvere i vettori di forza. Questo semplifica notevolmente la soluzione.

Collegare: Take-Home Investigation-Determination Friction from the Stopping Distance

Questo esperimento coinvolge la conversione dell’energia potenziale gravitazionale in energia termica. Usate il righello, il libro e la biglia della sezione “Making Connections” di Gravitational Potential Energy. Inoltre, avrete bisogno di una tazza di schiuma con un piccolo foro sul lato, come mostrato nella Figura 6. Dalla posizione di 10 cm sul righello, fate rotolare la biglia nella tazza posizionata alla base del righello. Misura la distanza d che la tazza si muove prima di fermarsi. Quali forze hanno causato l’arresto? Cosa è successo all’energia cinetica della biglia alla base del righello? Poi, metti la biglia nelle posizioni di 20 cm e 30 cm e misura di nuovo la distanza che la coppa si muove dopo che la biglia vi è entrata. Traccia la distanza che la coppa si muove rispetto alla posizione iniziale della biglia sul righello. Questa relazione è lineare?

Con alcune semplici ipotesi, puoi usare questi dati per trovare il coefficiente di attrito cinetico μk della tazza sul tavolo. La forza di attrito f sulla tazza è μkN, dove la forza normale N è solo il peso della tazza più la biglia. La forza normale e la forza di gravità non fanno lavoro perché sono perpendicolari allo spostamento della tazza, che si muove orizzontalmente. Il lavoro fatto dall’attrito è fd. Avrete bisogno anche della massa della biglia per calcolare la sua energia cinetica iniziale.

È interessante fare l’esperimento di cui sopra anche con una biglia di acciaio (o un cuscinetto a sfera). Rilasciandola dalle stesse posizioni sul righello come hai fatto con la biglia di vetro, la velocità di questa biglia d’acciaio è la stessa di quella della biglia in fondo al righello? La distanza della coppa è proporzionale alla massa delle biglie d’acciaio e di vetro?

Figura 6. Far rotolare una biglia lungo un righello in una tazza di schiuma.

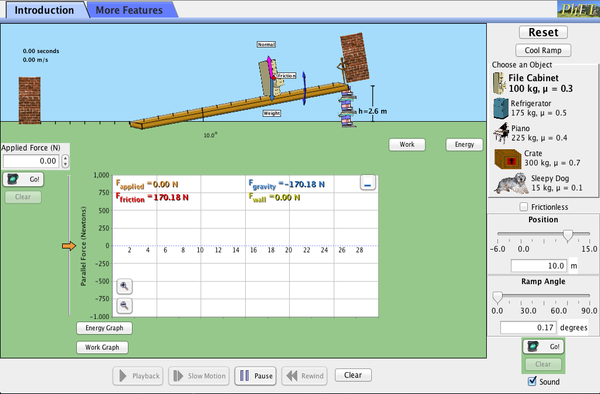
PhET Explorations: La rampa

Esplora forze, energia e lavoro mentre spingi oggetti domestici su e giù per una rampa. Abbassa e alza la rampa per vedere come l’angolo di inclinazione influenza le forze parallele che agiscono sullo schedario. I grafici mostrano forze, energia e lavoro.

Clicca per scaricare. Esegui usando Java.

Riassunto della sezione

• Una forza non conservativa è quella per cui il lavoro dipende dal percorso.
• L’attrito è un esempio di forza non conservativa che cambia l’energia meccanica in energia termica.
• Il lavoro Wnc fatto da una forza non conservativa cambia l’energia meccanica di un sistema. In forma di equazione, Wnc = ΔKE + ΔPE o, equivalentemente, KEi + PEi + Wnc = KEf + PEf.
• Quando agiscono sia forze conservative che non conservative, la conservazione dell’energia può essere applicata e usata per calcolare il moto in termini di energie potenziali note delle forze conservative e il lavoro fatto da forze non conservative, invece di trovare il lavoro netto dalla forza netta, o dover applicare direttamente le leggi di Newton.

Problemi & Esercizi

1. Uno sciatore di 60,0 kg con una velocità iniziale di 12,0 m/s risale un’altura alta 2,50 m come mostrato nella figura 7. Trova la sua velocità finale in cima, dato che il coefficiente di attrito tra i suoi sci e la neve è 0,0800. (Suggerimento: trovare la distanza percorsa lungo il pendio assumendo un percorso in linea retta come mostrato in figura.)
   

   Figura 7. L’energia cinetica iniziale dello sciatore è parzialmente utilizzata per raggiungere la cima di una salita.

2. (a) A che altezza può salire un’auto (motore disinnestato) se il lavoro fatto dall’attrito è trascurabile e la sua velocità iniziale è 110 km/h? (b) Se, nella realtà, un’auto di 750 kg con una velocità iniziale di 110 km/h viene osservata risalire una collina fino a un’altezza di 22,0 m sopra il suo punto di partenza, quanta energia termica è stata generata dall’attrito? (c) Qual è la forza media di attrito se la collina ha una pendenza di 2,5º sopra l’orizzontale?

Glossario

forza non conservativa: una forza il cui lavoro dipende dal percorso seguito tra la configurazione iniziale e quella finale date

attrito: la forza tra superfici che si oppone allo scorrimento di una sull’altra; l’attrito cambia l’energia meccanica in energia termica

Soluzioni selezionate ai problemi & Esercizi

1. 9,46 m/s