Les ordres du roi font un sacré casse-tête
(Difficulté : Facile)
Le roi Nupe du royaume Catan adore tellement ses deux filles qu’il décide que le royaume serait mieux avec plus de filles que de garçons, et il prend le décret suivant : Tous les couples en âge d’avoir des enfants devront continuer à en avoir jusqu’à ce qu’ils aient une fille !
Mais pour éviter la surpopulation, il fait un décret supplémentaire : Tous les couples en âge de procréer cesseront d’avoir des enfants dès qu’ils auront une fille ! Ses sujets commencent immédiatement à suivre ses ordres.
Après de nombreuses années, quelle est la proportion attendue de filles par rapport aux garçons à Catan ?
Introduction
La probabilité que chaque bébé qui naît soit une fille est, bien sûr, de 50 %.
Solution
Prête pour la solution ? Cliquez ici pour voir si vous avez raison.
Combien d’œufs cette poule pond-elle ?
(Difficulté : facile)
Ce problème est en l’honneur de mon père, Harold Feiveson. C’est grâce à lui que j’aime les énigmes mathématiques, et c’est l’un des premiers problèmes (parmi beaucoup d’autres) qu’il m’a donné en grandissant.
Une poule et demi pond un œuf et demi en un jour et demi. Combien d’œufs une poule pond-elle en un jour ?
Solution
Vous êtes prêt pour la solution ? Cliquez ici pour voir si vous avez raison.
Le problème mathématique de la chaîne en or est faussement simple
(Difficulté : modérée)
Vous fouillez dans le grenier de votre arrière-grand-mère quand vous trouvez cinq petites chaînes composées chacune de quatre maillons en or. Il vous vient à l’esprit que si vous les combiniez toutes en une grande boucle de 20 maillons, vous auriez un collier incroyable. Vous l’apportez donc chez une bijoutière, qui vous dit que le coût de fabrication du collier sera de 10 $ pour chaque maillon d’or qu’elle devra casser puis refermer.
Combien cela va-t-il coûter ?
Solution
Vous êtes prêt pour la solution ? Cliquez ici pour voir si vous avez raison.
Essayez de résoudre cette énigme de pickleball
(Difficulté : 🚨HARD🚨)
Kenny, Abby et Ned se sont réunis pour un tournoi de pickleball à la ronde, où, comme d’habitude, le gagnant reste après chaque partie pour jouer contre la personne qui s’est assise sur cette partie. À la fin de leur après-midi pickleball, Abby est épuisée, ayant joué les sept dernières parties consécutives. Kenny, qui est moins essoufflé, fait le décompte des parties jouées :
Kenny a joué huit parties
Abby a joué 12 parties
Ned a joué 14 parties
Qui a gagné la quatrième partie contre qui ?
Introduction
Combien de parties au total ont été jouées ?
Solution
Vous êtes prêts pour la solution ? Cliquez ici pour voir si vous avez raison.
Notre énigme du disjoncteur est purement diabolique. Désolé.
(Difficulté : 🚨HARD🚨)
Le boîtier de disjoncteurs de votre nouvelle maison se trouve dans un coin peu pratique de votre sous-sol. À votre grand dam, vous découvrez qu’aucun des 100 disjoncteurs n’est étiqueté, et vous êtes confronté à la perspective intimidante de faire correspondre chaque disjoncteur à sa lumière respective. (Supposons que chaque disjoncteur ne correspond qu’à une seule lumière.)
Pour commencer, vous allumez les 100 lumières de la maison, puis vous vous rendez dans votre sous-sol pour commencer le coûteux processus de cartographie. À chaque voyage dans votre sous-sol, vous pouvez allumer ou éteindre un nombre quelconque de disjoncteurs. Vous pouvez ensuite parcourir les couloirs de votre maison pour découvrir quelles lumières sont allumées et lesquelles sont éteintes.
Quel est le nombre minimum de voyages que vous devez faire au sous-sol pour cartographier chaque disjoncteur à chaque lumière ?
Introduction
La solution n’implique ni d’allumer ou d’éteindre les interrupteurs de votre maison, ni de sentir la chaleur des ampoules. Vous pourriez essayer de résoudre d’abord le cas de 10 disjoncteurs non étiquetés.
Solution
Préparé pour la solution ? Cliquez ici pour voir si vous avez raison.
Deux trains. Deux grands-mères. Pouvez-vous résoudre cette énigme mathématique difficile ?
(Difficulté : modérée)
Les deux grands-mères de Jesse veulent le voir tous les week-ends, mais elles vivent à l’opposé de la ville. En guise de compromis, il leur dit que tous les dimanches, il se rendra à la station de métro la plus proche de son appartement à une heure aléatoire de la journée et montera dans le prochain train qui arrivera.
Si c’est le train qui voyage vers le nord, il rendra visite à sa grand-mère Erica dans les quartiers chics, et si c’est le train qui voyage vers le sud, il rendra visite à sa grand-mère Cara dans le centre-ville. Ses deux grands-mères sont d’accord avec ce plan, car elles savent que les trains qui vont vers le nord et ceux qui vont vers le sud passent toutes les 20 minutes.
Mais après quelques mois à faire cela, Grand-mère Cara se plaint de ne le voir qu’un dimanche sur cinq. Jesse promet qu’il se rend effectivement à la gare à une heure aléatoire chaque jour. Comment est-ce possible ?
Introduction
Les trains arrivent toujours à l’heure prévue.
Solution
Prête pour la solution ? Cliquez ici pour voir si vous avez raison.
Voici un problème de mathématiques vraiment F@*#ing Hard sur les fourmis
(Difficulté : 🚨HARD🚨)
Max et Rose sont des frères et sœurs fourmis. Ils adorent faire la course l’un contre l’autre, mais sont toujours à égalité, car ils rampent en fait exactement à la même vitesse. Ils décident donc de créer une course où l’un d’entre eux (avec un peu de chance) gagnera.
Pour cette course, chacun d’entre eux commencera au coin inférieur d’un cuboïde, puis rampera aussi vite que possible pour atteindre une miette au coin opposé. Les mesures de leurs cuboïdes sont celles de l’image:
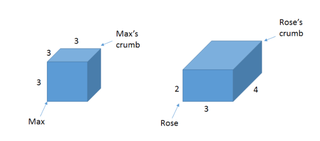
Si elles empruntent toutes deux le chemin le plus court possible pour atteindre leur miette, qui atteindra sa miette en premier ? (N’oubliez pas que ce sont des fourmis, donc elles peuvent bien sûr grimper n’importe où sur les bords ou la surface du cuboïde.)
Introduction
Rappellez-vous : Pensez en dehors de la boîte.
Solution
Préparé pour la solution ? Cliquez ici pour voir si vous avez raison.
Cette énigme de Peppermint Patty est pratiquement impossible
(Difficulté : 🚨HARD🚨)
Vous êtes face à votre amie, Caryn, dans un « candy-off », qui fonctionne comme suit : Il y a une pile de 100 caramels et une pastille de menthe poivrée. Vous et Caryn allez aller et venir en prenant au moins un et pas plus de cinq caramels de la pile de bonbons à chaque tour. La personne qui retire le dernier caramel recevra également la galette de menthe poivrée. Et vous adorez les galettes à la menthe poivrée.
Supposons que Caryn vous laisse décider qui commence. Qui devriez-vous choisir afin d’être sûr de gagner la galette à la menthe poivrée ?
Introduction
D’abord, résolvez le problème pour une pile de 10 caramels.
Solution
Préparé pour la solution ? Cliquez ici pour voir si vous avez raison.
Pouvez-vous résoudre l’énigme du Great American Rail-Trail ?
(Difficulté : modérée)
Ce problème a été suggéré par le physicien P. Jeffrey Ungar.
Enfin, le Great American Rail-Trail qui traverse tout le pays est terminé ! Allez-y, tapez-vous dans le dos : vous venez d’installer la plus longue main courante de l’histoire du monde, avec 4 000 miles de bout en bout. Mais juste après la cérémonie d’ouverture, votre assistant vous rappelle que le métal que vous avez utilisé pour la main courante se dilate légèrement en été, de sorte que sa longueur augmentera d’un pouce au total.
« Ha ! », dites-vous, « Un pouce sur une main courante de 4 000 miles ? Ce n’est rien ! » Mais… avez-vous raison ?
Supposons que lorsque la main courante se dilate, elle se déforme vers le haut à son point le plus faible, qui se trouve au centre. De combien de hauteur les piétons du milieu du pays devront-ils s’élever en été pour attraper la main courante ? Autrement dit, dans la figure ci-dessous, quelle est h ? (Pour les besoins de cette question, ignorez la courbure de la Terre et supposez que le sentier est une ligne droite.)
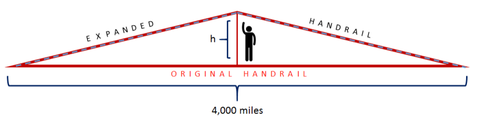
Introduction
Pythagore est un personnage historique fascinant.
Solution
Préparé pour la solution ? Cliquez ici pour voir si vous avez raison.
Cette énigme ressemble à un problème de SAT particulièrement cruel. Pouvez-vous trouver la réponse ?
(Difficulté : modérée)
Amanda vit avec son fils adolescent, Matt, à la campagne – à une distance en voiture de l’école de Matt. Chaque après-midi, Amanda quitte la maison à la même heure, se rend à l’école à une vitesse constante, récupère Matt exactement à l’heure où son club d’échecs se termine à 17 heures, puis ils rentrent immédiatement ensemble à la maison à la même vitesse constante. Mais un jour, Matt ne se sent pas bien, alors il quitte l’entraînement d’échecs plus tôt et commence à rentrer chez lui sur son scooter portable.
Après que Matt ait fait du scooter pendant une heure, Amanda le croise dans sa voiture (sur son trajet habituel pour le récupérer), et ils rentrent ensemble, arrivant chez eux 40 minutes plus tôt que d’habitude. Combien d’entraînement aux échecs Matt a-t-il manqué ?
Introduction
Envisagez le cas où Amanda rencontre Matt exactement au moment où elle quitte leur maison.
Solution
Prête pour la solution ? Cliquez ici pour voir si vous avez raison.
Pouvez-vous faire traverser la rivière à ces 3 stars du cinéma ?
(Difficulté : modérée)
Trois stars du cinéma, Chloé, Lexa et Jon, tournent un film en Amazonie. Ils sont très célèbres et très exigeants, donc leurs agents sont toujours avec eux. Un jour, après avoir tourné une scène au cœur de la forêt tropicale, les trois acteurs et leurs agents décident de rentrer à pied à la base. Soudain, ils arrivent à une grande rivière.
Sur la berge, ils trouvent une petite barque, mais elle est seulement assez grande pour contenir deux d’entre eux à la fois. Le piège ? Aucun des agents n’est à l’aise à l’idée de laisser sa star de cinéma à d’autres agents s’ils ne sont pas là aussi. Ils n’ont pas confiance dans le fait que les autres agents ne vont pas essayer de débaucher leur star.
Par exemple, l’agent de Chloé est d’accord si Chloé et Lexa sont seules dans le bateau ou sur l’une des rives, mais certainement pas d’accord si l’agent de Lexa est aussi avec elles. Alors comment peuvent-elles toutes traverser la rivière ?
Introduction
Il n’y a pas qu’une seule façon de résoudre ce problème.
Solution
Prête pour la solution ? Cliquez ici pour voir si vous avez raison.
Cette énigme ridiculement difficile est notre hommage à un génie des mathématiques décédé. Pouvez-vous la résoudre ?
(Difficulté : 🚨HARD🚨)
Le 11 avril, John Horton Conway, un brillant mathématicien qui avait un amour intense et ludique des énigmes et des jeux, est décédé des complications du COVID-19. Conway est l’inventeur de l’un de mes problèmes légendaires préférés (à ne pas prendre à la légère) et du célèbre jeu de la vie. J’ai créé ce problème en son honneur.
Carol créait un arbre généalogique, mais avait du mal à retrouver la date de naissance de sa mère. Le seul indice qu’elle a trouvé est une lettre écrite par son grand-père à sa grand-mère le jour de la naissance de sa mère. Malheureusement, certains caractères ont été effacés, représentés ici par un « ___ ». (La longueur de la ligne ne reflète pas le nombre de caractères maculés.)
« Chère Virginia,
J’étais loin de me douter, en me rendant au travail ce lundi matin, que le soir même, nous aurions une magnifique petite fille. Et le jour de notre anniversaire de mariage, pas moins ! Cela me fait penser à cette incroyable journée de week-end, le 27 J___ 19___, lorsque nous avons partagé pour la première fois notre vœu de créer une famille ensemble, et, eh bien, nous sommes là ! Joyeux huitième anniversaire, mon amour.
Amour, Edwin »
La question : Quand est née la mère de Carol ?
Introduction
Ce problème est inspiré de la règle du Jugement dernier de Conway.
Solution
Prête pour la solution ? Cliquez ici pour voir si vous avez raison.
Pour résoudre cette énigme mathématique tordue, il vous suffit d’une ceinture et d’une terre
(Difficulté : modérée)
Imaginez que vous avez une très longue ceinture. Eh bien, extrêmement longue, vraiment… en fait, elle est juste assez longue pour pouvoir s’enrouler confortablement autour de la circonférence de notre planète entière. (Pour simplifier, supposons que la Terre est parfaitement ronde, sans montagnes, océans ou autres obstacles sur le chemin de la ceinture.)
Naturellement, vous êtes très fier de votre ceinture. Mais voilà que votre frère, Pierre, se présente – et à votre grand dam, il produit une ceinture qui est juste un peu plus longue que la vôtre. Il se vante que sa ceinture est plus longue d’exactement sa taille : 1,80 m.
Si Peter devait également enrouler sa ceinture autour de la circonférence de la Terre, à quelle distance au-dessus de la surface pourrait-il suspendre la ceinture s’il la tirait de manière tendue et uniforme ?
Introduction
La circonférence de la Terre est d’environ 25 000 miles, soit 130 millions de pieds… mais vous n’avez pas besoin de le savoir pour résoudre ce problème.
Solution
Prêts pour la solution ? Cliquez ici pour voir si vous avez raison.
Cette énigme du tapotement du coude est diabolique. Bonne chance pour la résoudre.
(Difficulté : 🚨HARD🚨)
Dans un temps futur, lorsque les interdictions d’abri sur place sont levées, un couple marié, Florian et Julia, se rend dans un bar pour célébrer leur liberté retrouvée.
Ils y trouvent quatre autres couples qui ont eu la même idée.
Envie de contacts sociaux, chaque personne des cinq couples tape avec enthousiasme du coude (la nouvelle poignée de main) à chaque personne qu’elle n’a pas encore rencontrée.
Il s’avère en fait que beaucoup de personnes se connaissaient déjà auparavant, si bien que lorsque Julia demande à chacun combien de coudes il a tapé, elle obtient remarquablement neuf réponses différentes !
La question : Combien de coudes Florian a-t-il tapé ?
L’indice
Quelles sont les neuf réponses que Julia a entendues ?
Solution
Vous êtes prêts pour la solution ? Cliquez ici pour voir si vous avez raison.
Vous aurez besoin d’un verre après avoir essayé de résoudre cette énigme du whisky
(Difficulté : facile)
Alan et Claire vivent selon le vieux dicton écossais : « Ne jamais avoir de whisky sans eau, ni d’eau sans whisky ! » Ainsi, un jour, alors qu’Alan a devant lui un verre de whisky, et que Claire a devant elle un verre d’eau de même taille, Alan prend une cuillère de son whisky et la met dans l’eau de Claire.
Claire remue son eau teintée de whisky, puis remet une cuillère de ce mélange dans le whisky d’Alan pour s’assurer qu’ils ont exactement la même quantité à boire.
Alors : Y a-t-il plus d’eau dans le whisky d’Alan, ou plus de whisky dans l’eau de Claire ? Et est-ce important que Claire ait bien remué ?
Introduction
La taille de la cuillère n’a pas d’importance.
Solution
Prête pour la solution ? Cliquez ici pour voir si vous avez raison.
Le problème du gribouillage est beaucoup plus difficile qu’il n’y paraît. Pouvez-vous le résoudre ?
(Difficulté : modérée)
L’énigme de cette semaine est relativement simple – mais sinistre tout de même.
La question : Pouvez-vous faire 100 en intercalant un nombre quelconque de plus et de moins dans la chaîne de chiffres 9 8 7 6 5 4 3 2 1 ? Vous ne pouvez pas changer l’ordre des chiffres ! Alors quel est le plus petit nombre de plus et de moins nécessaire pour faire 100 ?
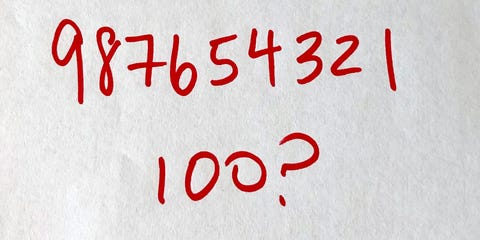
Par exemple, 98 – 7 – 6 + 54 – 32 montre une façon d’intercaler les plus et les moins, mais comme cela donne 107, ce n’est pas une solution.
J’appelle cela un » problème de gribouillage » : un problème sur lequel il est préférable de travailler pendant les réunions où vous pourriez gribouiller autrement.
Introduction
Vous pourriez commencer à chercher des solutions qui utilisent un total de sept plus et moins (bien qu’il existe des façons d’en utiliser moins).
Solution
Prête pour la solution ? Cliquez ici pour voir si vous avez raison.
Cette énigme mathématique a déconcerté tous les scientifiques sauf un. Pensez-vous pouvoir la résoudre ?
(Difficulté : HARD)
En l’honneur de Freeman Dyson, le célèbre physicien décédé le mois dernier, voici un récit légendaire démontrant sa vivacité d’esprit et son incroyable puissance cérébrale.
Un jour, lors d’une réunion de scientifiques de haut niveau, l’un d’entre eux s’est demandé à voix haute s’il existe un nombre entier que l’on peut exactement doubler en déplaçant son dernier chiffre vers l’avant. Par exemple, 265 y répondrait si 526 était son double exact – ce qui n’est pas le cas.
Après apparemment seulement cinq secondes, Dyson a répondu : « Bien sûr qu’il existe, mais le plus petit de ces nombres a 18 chiffres. »
Cela a laissé certains des scientifiques les plus intelligents du monde perplexes quant à la façon dont il a pu comprendre cela si rapidement.
Alors, étant donné l’indice de Dyson, quel est le plus petit de ces nombres ?
Introduction
Mon élève de CE1 a récemment appris à ajouter un nombre à 3 chiffres à lui-même en utilisant la méthode verticale classique :

Les nombres à 18 chiffres, bien sûr, peuvent être ajoutés de la même manière.
Solution
Prête pour la solution ? Cliquez ici pour voir si vous avez raison.
Découvrez ce qu’il y a sur son front
(Difficulté : modérée)
Cécilia adore tester la logique de ses amis très logiques Jaya, Julian et Levi, alors elle annonce :
« Je vais écrire un nombre positif sur chacun de vos fronts. Aucun des nombres n’est le même, et deux des nombres s’additionnent au troisième. »
Elle griffonne les nombres sur leurs têtes, puis se tourne vers Jaya et lui demande quel est son nombre. Jaya voit que Julian a 20 sur son front et que Levi a 30 sur le sien. Elle réfléchit un moment et dit : « Je ne sais pas quel est mon numéro ». Julian ajoute : « Je ne connais pas non plus mon numéro », puis Levi s’exclame : « Moi non plus ! ». Cecilia se réjouit : « Je vous ai enfin fait tomber les gars ! »
« Pas si vite ! » Jaya dit. « Maintenant, je connais mon numéro ! »
Quel est le numéro de Jaya ?
Introduction
Jaya pourrait être l’un de deux numéros, mais un seul de ces numéros conduirait à ce que Julian et Levi ne connaissent pas tous les deux leur numéro. Pourquoi ?
Solution
Préparé pour la solution ? Cliquez ici pour voir si vous avez raison.
Pouvez-vous faire élire Keanu Reeves comme président ?
(Difficulté : modérée)
Nous sommes en 2024, et cinq candidats se présentent aux primaires démocratiques : Taylor Swift, Oprah Winfrey, Mark Cuban, Keanu Reeves et Dwayne Johnson. (Hé, ça pourrait arriver.) Comme d’habitude, la première primaire a lieu dans l’Iowa.
Dans un effort pour surmonter son embarras après la débâcle des caucus de 2020, le parti démocrate de l’Iowa vient d’annoncer une nouvelle méthode infaillible pour trouver le meilleur candidat : il y aura quatre élections consécutives.
D’abord, le candidat 1 se présentera contre le candidat 2. Ensuite, le gagnant de cette élection se présentera contre le candidat 3, puis ce gagnant se présentera contre le candidat 4, et enfin le gagnant de cette élection se présentera contre le dernier candidat. Par la propriété transitive, le gagnant de cette dernière élection doit être le meilleur candidat… c’est ce que dit le parti démocrate de l’Iowa.
Le candidat Keanu se sent plutôt déprimé, car il sait qu’il est classé près du bas de l’échelle par la plupart des électeurs, et au sommet par aucun. En fait, il sait que la population de l’Iowa est divisée en cinq groupes égaux, et que leurs préférences sont les suivantes :

Keanu est ami d’enfance avec Bill S. Preston, Esq., le nouveau chef du parti démocrate de l’Iowa. Preston, persuadé que l’ordre des candidats n’a pas d’importance pour le résultat, dit à Keanu qu’il peut choisir l’ordre de vote des candidats.
Alors, quel ordre Keanu devrait-il choisir ?
Introduction
Comment Keanu s’en sortirait-il dans des courses en tête-à-tête contre chaque candidat ?
Solution
Prête pour la solution ? Cliquez ici pour voir si vous avez raison.
Qui a ouvert tous ces fichus casiers ?
(Difficulté : modérée)
Il y a 100 casiers qui bordent le couloir principal du lycée de Chelm. Chaque soir, le directeur de l’école s’assure que tous les casiers sont fermés afin qu’il y ait un début ordonné pour le lendemain. Un jour, 100 élèves malicieux décident de faire une farce.
Les élèves se retrouvent tous avant le début des cours et se mettent en rang. Le premier élève marche ensuite dans le couloir et ouvre tous les casiers. L’élève suivant suit en fermant tous les autres casiers (en commençant par le deuxième casier). L’élève 3 se rend ensuite à chaque troisième casier (en commençant par le troisième) et l’ouvre s’il est fermé, et le ferme s’il est ouvert. L’élève 4 suit en ouvrant chaque quatrième casier s’il est fermé et en le fermant s’il est ouvert. Et ainsi de suite jusqu’à ce que l’élève 100 se rende enfin au centième casier. Lorsque la directrice arrive plus tard dans la matinée, quels casiers trouve-t-elle ouverts ?
Introduction
Assurez-vous de prêter attention à tous les facteurs.
Solution
Vous êtes prêt pour la solution ? Cliquez ici pour voir si vous avez raison.
.