Darrell Henry, Université d’État de Louisiane
Nelson Eby, Université du Massachusetts – Lowell
John Goodge, Université du Minnesota – Duluth
David Mogk, Montana State University
Lorsqu’un cristal est bombardé de rayons X d’une longueur d’onde fixe (similaire à l’espacement des plans du réseau cristallin à l’échelle atomique) et sous certains angles d’incidence, des rayons X réfléchis intenses sont produits lorsque les longueurs d’onde des rayons X diffusés interfèrent de manière constructive. Pour que les ondes interfèrent de manière constructive, les différences dans le trajet de déplacement doivent être égales à des multiples entiers de la longueur d’onde. Lorsque cette interférence constructive se produit, un faisceau diffracté de rayons X quittera le cristal à un angle égal à celui du faisceau incident.
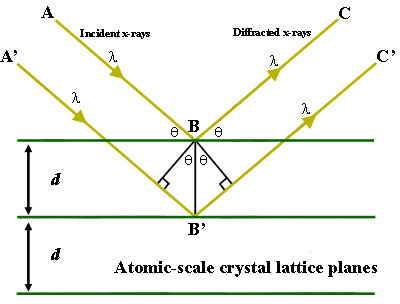
Figure 1. Réflexion selon la loi de Bragg. Les rayons X diffractés présentent une interférence constructive lorsque la distance entre les chemins ABC et A’B’C’ diffère d’un nombre entier de longueurs d’onde (λ).
Pour illustrer cette caractéristique, considérons un cristal dont les distances planes du réseau cristallin d (à droite). Lorsque la différence de longueur de trajet entre les trajets des rayons ABC et A’B’C’ est un multiple entier de la longueur d’onde, une interférence constructive se produira pour une combinaison de cette longueur d’onde spécifique, de l’espacement planaire du réseau cristallin et de l’angle d’incidence (Θ). Chaque plan rationnel d’atomes dans un cristal subira une réfraction à un seul et unique angle (pour des rayons X de longueur d’onde fixe).
La relation générale entre la longueur d’onde des rayons X incidents, l’angle d’incidence et l’espacement entre les plans du réseau cristallin des atomes est connue sous le nom de loi de Bragg, exprimée comme suit :
n λ = 2d sinΘ
où n (un nombre entier) est l' »ordre » de réflexion, λ est la longueur d’onde des rayons X incidents, d est l’espacement interplanaire du cristal et Θ est l’angle d’incidence.
Applications de la loi de Bragg.
- Dans la diffraction des rayons X (XRD), l’espacement interplanaire (espacement d) d’un cristal est utilisé à des fins d’identification et de caractérisation. Dans ce cas, la longueur d’onde du rayon X incident est connue et on mesure l’angle d’incidence (Θ) auquel se produit l’interférence constructive. La résolution de l’équation de Bragg donne l’espacement d entre les plans du réseau cristallin des atomes qui produisent l’interférence constructive. On s’attend à ce qu’un cristal inconnu donné ait de nombreux plans rationnels d’atomes dans sa structure ; par conséquent, la collection de » réflexions » de tous les plans peut être utilisée pour identifier de manière unique un cristal inconnu. En général, les cristaux à haute symétrie (par exemple, le système isométrique) ont tendance à avoir relativement peu de plans atomiques, tandis que les cristaux à faible symétrie (dans les systèmes triclinique ou monoclinique) ont tendance à avoir un grand nombre de plans atomiques possibles dans leurs structures.
- Dans le cas de la spectrométrie dispersive en longueur d’onde (WDS) ou de la spectroscopie de fluorescence X (XRF), des cristaux d’espacements d connus sont utilisés comme cristaux d’analyse dans le spectromètre. Comme la position de l’échantillon et du détecteur est fixe dans ces applications, la position angulaire du cristal réflecteur est modifiée conformément à la loi de Bragg de façon à ce qu’une longueur d’onde particulière puisse être dirigée vers un détecteur pour une analyse quantitative. Chaque élément du tableau périodique présente une différence d’énergie discrète entre les « coquilles » orbitales (par exemple K, L, M), de sorte que chaque élément produit des rayons X d’une longueur d’onde fixe. Par conséquent, en utilisant un cristal de spectromètre (avec un espacement d fixe du cristal) et en positionnant le cristal à un angle unique et fixe (Θ), il est possible de détecter et de quantifier les éléments d’intérêt en fonction des longueurs d’onde de rayons X caractéristiques produites par chaque élément.
Littérature
Eby, G.N., 2004, Principles of Environmental Geochemistry. Brooks/Cole-Thomson Learning, p. 212-214.