Se il numero di fessure in un ostacolo è grande la nitidezza del modello migliora, i massimi diventano più stretti. Gli ostacoli con un gran numero di fessure (più di, diciamo, 20 al millimetro) sono chiamati reticoli di diffrazione. Questi furono sviluppati per la prima volta da Fraunhofer alla fine del diciottesimo secolo e consistevano in un sottile filo d’argento avvolto su due viti parallele che davano circa 30 ostacoli al millimetro.
Da allora sono stati fatti molti miglioramenti, nel 1882 Rowland ha usato un diamante per regolare linee sottili sul vetro, le creste agendo come fessure e le righe come ostacoli (Vedi Figura 1). Usando questo metodo è possibile ottenere reticoli di diffrazione con fino a 3000 linee per millimetro, anche se reticoli ‘grossolani’ con circa 500 linee per millimetro sono migliori per l’uso generale.
In molte scuole due tipi sono di uso comune, uno con 300 linee per mm e l’altro con 80 linee per mm.
Si usano anche reticoli a riflessione, dove l’immagine diffratta viene vista dopo la riflessione da una superficie rigata. Un ottimo esempio di un reticolo di diffrazione a riflessione è un CD. Un DVD con righe più sottili dà un modello di diffrazione molto più ampio.
La teoria delle onde e il reticolo di diffrazione
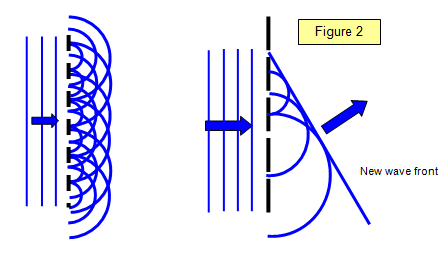
La figura 2 mostra la costruzione di Huygens per un reticolo. Si può vedere come le onde diffratte circolari da ogni fenditura si sommano in certe direzioni per dare un’onda diffratta che ha un fronte d’onda piano proprio come le onde che colpiscono il reticolo da sinistra. Questa onda piana si forma tracciando la linea che incontra tutte le piccole onde circolari e si chiama inviluppo di tutte queste piccole onde secondarie.
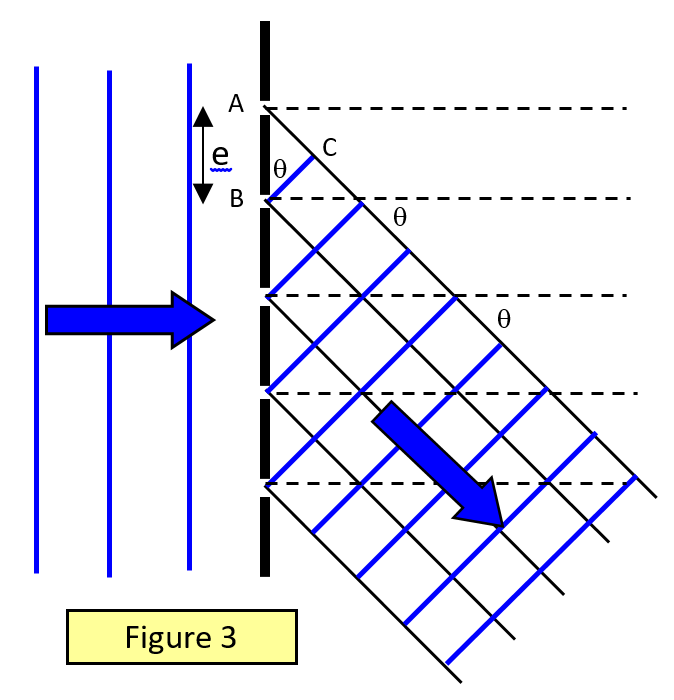
La formula del reticolo di diffrazione
Considera un fascio di luce parallelo incidente normalmente su un reticolo di diffrazione con una spaziatura e (la spaziatura del reticolo è l’inverso del numero di linee per unità di lunghezza). Consideriamo la luce che viene diffratta con un angolo q rispetto alla normale e che proviene da punti corrispondenti su fessure adiacenti (Figura 3).
Per un massimo la differenza di percorso = AC = mλ
Ma AC = e sinθ. Quindi per un massimo:
mλ = e sinθ
dove m = 0, 1, 2,3…
Il numero m è noto come l’ordine dello spettro, cioè, uno spettro di primo ordine è formato per m = 1, e così via.
Se si usa luce di una singola lunghezza d’onda, come quella di un laser, allora si verifica una serie di linee nitide, una linea per ogni ordine dello spettro. Con una sorgente di luce bianca si forma una serie di spettri con la luce della lunghezza d’onda più corta che ha il più piccolo angolo di diffrazione.
Nella derivazione della formula di cui sopra, abbiamo assunto che il fascio incidente è ad angolo retto rispetto alla faccia della griglia. Se questo non è il caso, bisogna tenerne conto. Il modo più semplice è quello di misurare la posizione dello spettro del primo ordine su entrambi i lati del centro, registrare l’angolo tra queste posizioni e poi dimezzarlo, come mostrato nella figura 4.
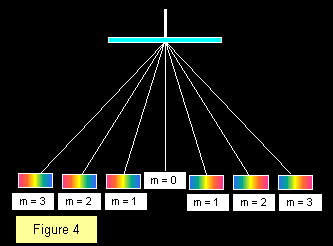
Il numero di ordini di spettri visibili con una data griglia dipende dalla spaziatura della griglia, più spettri sono visibili con griglie più grosse. La faccia rigata del reticolo dovrebbe sempre puntare lontano dalla luce incidente per evitare errori dovuti ai cambiamenti di direzione a causa della rifrazione nel vetro. Il diagramma mostra una frangia bianca centrale con tre spettri su entrambi i lati per un totale di sette immagini.
(Vedi problema di esempio)
1. Calcolare la lunghezza d’onda della luce monocromatica in cui l’immagine del secondo ordine viene diffratta attraverso un angolo di 25o utilizzando un reticolo di diffrazione con 300 linee per millimetro.
Spaziatura del reticolo (e) = 10-3/300 m = 3.3×10-6 m
Lunghezza d’onda (l) = esin25/2 = /2 = 6,97×10-7 m = 697 nm
2. Calcolare il numero massimo di ordini visibili con un reticolo di diffrazione di 500 linee per millimetro, usando luce di lunghezza d’onda 600 nm.
Angolo massimo di diffrazione = 90o e = 10-3/500 = 2×10-6 m
Pertanto m = esinq/l = 2×10-6/600×10-9 = 3,33
Pertanto numero massimo di ordini = 3, e un totale di sette immagini della sorgente può essere visto (tre su ogni lato di un’immagine centrale).
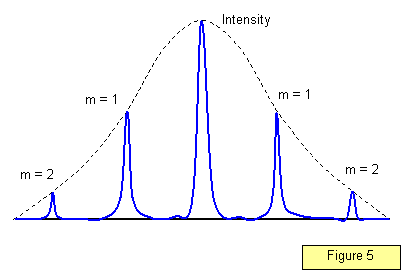
La distribuzione dell’intensità nel modello di diffrazione per un gran numero di fessure è mostrata in Figura 5. Si noti che i massimi diventano molto più netti; maggiore è il numero di fenditure per metro, meglio definiti sono i massimi.
La diffrazione della luce al cadmio o al mercurio è usata per determinare la separazione di due linee su un circuito integrato. I seguenti risultati sono stati ottenuti per le immagini diffratte del secondo ordine per diverse lunghezze d’onda. Usateli per tracciare un grafico lineare appropriato e quindi determinare la distanza media dei fili sul circuito.
| Lunghezza d’onda/nm | Angolo di diffrazione (o) |
| 468 | 28.0 |
| 480 | 28.7 |
| 509 | 31.0 |
| 546 | 33.0 |
| 577 | 35.5 |
| 644 | 40.0 |