⇐ Argomento precedente|Assunto ⇒ Indice
Prima di fare un esperimento, si dovrebbe eseguire un’analisi di potenza per stimare il numero di osservazioni necessarie per avere una buona probabilità di rilevare l’effetto che si sta cercando.
Introduzione
Quando stai progettando un esperimento, è una buona idea stimare la dimensione del campione di cui avrai bisogno. Questo è particolarmente vero se state proponendo di fare qualcosa di doloroso per gli esseri umani o altri vertebrati, dove è particolarmente importante minimizzare il numero di individui (senza rendere la dimensione del campione così piccola che l’intero esperimento sia uno spreco di tempo e sofferenza), o se state progettando un esperimento molto lungo o costoso. Sono stati sviluppati metodi per molti test statistici per stimare la dimensione del campione necessaria per rilevare un particolare effetto, o per stimare la dimensione dell’effetto che può essere rilevato con una particolare dimensione del campione.
Per fare un’analisi di potenza, è necessario specificare una dimensione dell’effetto. Questa è la dimensione della differenza tra l’ipotesi nulla e l’ipotesi alternativa che si spera di rilevare. Per la ricerca biologica applicata e clinica, ci può essere una dimensione dell’effetto molto definita che si vuole rilevare. Per esempio, se stai testando un nuovo shampoo per cani, il dipartimento di marketing della tua azienda potrebbe dirti che produrre il nuovo shampoo sarebbe utile solo se rendesse il pelo dei cani almeno il 25% più lucido, in media. Questa sarebbe la vostra dimensione dell’effetto, e la usereste per decidere quanti cani dovreste sottoporre al riflettometro canino.
Quando si fa una ricerca biologica di base, spesso non si sa quanto sia grande la differenza che si sta cercando, e la tentazione potrebbe essere quella di usare la dimensione del campione più grande che ci si può permettere, o di usare un campione simile a quello di altre ricerche nel vostro campo. Dovresti comunque fare un’analisi della potenza prima di fare l’esperimento, solo per avere un’idea di che tipo di effetti potresti rilevare. Per esempio, alcuni fanatici anti-vaccinazione hanno proposto che il governo degli Stati Uniti conduca un grande studio su bambini non vaccinati e vaccinati per vedere se i vaccini causano l’autismo. Non è chiaro quale dimensione dell’effetto sarebbe interessante: 10% di autismo in più in un gruppo? 50% in più? il doppio? Tuttavia, facendo un’analisi della potenza mostra che anche se lo studio includesse ogni bambino non vaccinato negli Stati Uniti dai 3 ai 6 anni, e un numero uguale di bambini vaccinati, ci dovrebbe essere il 25% di autismo in più in un gruppo per avere un’alta probabilità di vedere una differenza significativa. Uno studio più plausibile, di 5.000 bambini non vaccinati e 5.000 vaccinati, rileverebbe una differenza significativa con alta potenza solo se ci fosse tre volte più autismo in un gruppo che nell’altro. Poiché è improbabile che ci sia una differenza così grande nell’autismo tra bambini vaccinati e non vaccinati, e poiché non trovare una relazione con un tale studio non convincerebbe i fanatici anti-vaccinazione che non c’è alcuna relazione (niente li convincerebbe che non c’è alcuna relazione – è questo che li rende fanatici), l’analisi di potenza vi dice che uno studio così grande e costoso non sarebbe utile.
Parametri
Ci sono quattro o cinque numeri coinvolti in una analisi di potenza. Devi scegliere i valori per ognuno di essi prima di fare l’analisi. Se non hai una buona ragione per usare un particolare valore, puoi provare diversi valori e guardare l’effetto sulla dimensione del campione.
Dimensione dell’effetto
La dimensione dell’effetto è la deviazione minima dall’ipotesi nulla che speri di rilevare. Per esempio, se stai trattando le galline con qualcosa che speri cambi il rapporto tra i sessi dei loro pulcini, potresti decidere che il cambiamento minimo nella proporzione dei sessi che stai cercando è del 10%. Si direbbe quindi che la dimensione dell’effetto è del 10%. Se state testando qualcosa per far sì che le galline depongano più uova, la dimensione dell’effetto potrebbe essere di 2 uova al mese.
Occasione, avrete una buona ragione economica o clinica per scegliere una particolare dimensione dell’effetto. Se state testando un integratore di mangime per polli che costa 1,50 dollari al mese, siete interessati solo a scoprire se produrrà più di 1,50 dollari di uova in più ogni mese; sapere che un integratore produce 0,1 uova in più al mese non è un’informazione utile per voi, e non avete bisogno di progettare il vostro esperimento per scoprirlo. Ma per la maggior parte delle ricerche biologiche di base, la dimensione dell’effetto è solo un bel numero tondo che hai tirato fuori dal culo. Diciamo che stai facendo un’analisi di potenza per uno studio su una mutazione in una regione promotrice, per vedere se influenza l’espressione genica. Quanto grande è il cambiamento nell’espressione genica che state cercando: 10%? 20%? 50%? È un numero piuttosto arbitrario, ma avrà un effetto enorme sul numero di topi transgenici che daranno le loro costose piccole vite per la vostra scienza. Se non avete una buona ragione per cercare una particolare dimensione dell’effetto, potreste anche ammetterlo e disegnare un grafico con la dimensione del campione sull’asse X e la dimensione dell’effetto sull’asse Y. G*Power lo farà per voi.
Alpha
Alpha è il livello di significatività del test (il valore P), la probabilità di rifiutare l’ipotesi nulla anche se è vera (un falso positivo). Il valore usuale è alfa=0,05. Alcuni calcolatori di potenza usano l’alfa a una coda, il che confonde, dato che l’alfa a due code è molto più comune. Assicuratevi di sapere quale state usando.
Beta o potenza
Beta, in un’analisi di potenza, è la probabilità di accettare l’ipotesi nulla, anche se è falsa (un falso negativo), quando la differenza reale è uguale alla dimensione minima dell’effetto. La potenza di un test è la probabilità di rifiutare l’ipotesi nulla (ottenere un risultato significativo) quando la differenza reale è uguale alla dimensione minima dell’effetto. La potenza è 1-beta. Non c’è un chiaro consenso sul valore da usare, quindi questo è un altro numero che si tira fuori dal sedere; una potenza dell’80% (equivalente a un beta del 20%) è probabilmente la più comune, mentre alcune persone usano il 50% o il 90%. Il costo per voi di un falso negativo dovrebbe influenzare la vostra scelta della potenza; se volete davvero, davvero essere sicuri di rilevare la vostra dimensione dell’effetto, vorrete usare un valore più alto per la potenza (beta più basso), che risulterà in una dimensione del campione più grande. Alcuni calcolatori di potenza vi chiedono di inserire beta, mentre altri chiedono la potenza (1-beta); siate molto sicuri di capire quale dovete usare.
Deviazione standard
Per le variabili di misura, avete anche bisogno di una stima della deviazione standard. Quando la deviazione standard diventa più grande, diventa più difficile rilevare una differenza significativa, quindi avrete bisogno di un campione più grande. La vostra stima della deviazione standard può provenire da esperimenti pilota o da esperimenti simili nella letteratura pubblicata. È improbabile che la deviazione standard, una volta fatto l’esperimento, sia esattamente la stessa, quindi il vostro esperimento sarà in realtà un po’ più o meno potente di quanto avevate previsto.
Per le variabili nominali, la deviazione standard è una semplice funzione della dimensione del campione, quindi non è necessario stimarla separatamente.
Come funziona
I dettagli di un’analisi di potenza sono diversi per diversi test statistici, ma i concetti di base sono simili; qui userò il test binomiale esatto come esempio. Immaginate di studiare le fratture del polso, e la vostra ipotesi nulla è che metà delle persone che si rompono un polso si rompono il polso destro, e metà si rompono il sinistro. Decidete che la dimensione minima dell’effetto è 10%; se la percentuale di persone che si rompono il polso destro è 60% o più, o 40% o meno, volete avere un risultato significativo dal test binomiale esatto. Non ho idea del perché tu abbia scelto il 10%, ma è quello che userai. Alpha è il 5%, come al solito. Volete che la potenza sia del 90%, il che significa che se la percentuale di polsi destri rotti è davvero del 40% o 60%, volete una dimensione del campione che dia un risultato significativo (P<0.05) il 90% delle volte, e un risultato non significativo (che sarebbe un falso negativo in questo caso) solo il 10% delle volte.
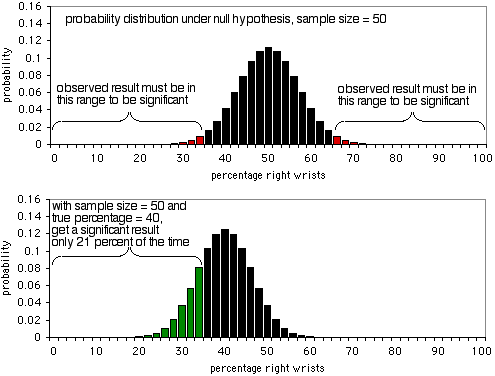

Il primo grafico mostra la distribuzione di probabilità sotto l’ipotesi nulla, con una dimensione del campione di 50 individui. Se l’ipotesi nulla è vera, vedrete meno del 36% o più del 64% di persone che si rompono il polso destro (un falso positivo) circa il 5% delle volte. Come mostra il secondo grafico, se la percentuale vera è il 40%, i dati del campione saranno meno del 36 o più del 64% solo il 21% delle volte; si otterrebbe un vero positivo solo il 21% delle volte, e un falso negativo il 79% delle volte. Ovviamente, una dimensione del campione di 50 è troppo piccola per questo esperimento; darebbe un risultato significativo solo il 21% delle volte, anche se c’è un rapporto 40:60 di polsi destri rotti rispetto ai polsi sinistri.
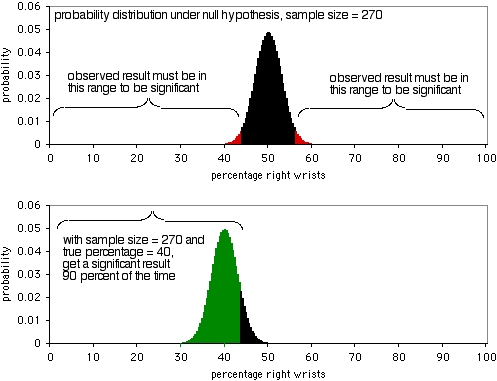

Il prossimo grafico mostra la distribuzione di probabilità sotto l’ipotesi nulla, con una dimensione del campione di 270 individui. Per essere significativo al livello P<0,05, il risultato osservato dovrebbe essere inferiore al 43,7% o superiore al 56,3% delle persone che si rompono il polso destro. Come mostra il secondo grafico, se la percentuale vera è del 40%, i dati del campione saranno così estremi il 90% delle volte. Un campione di 270 persone è abbastanza buono per questo esperimento; darebbe un risultato significativo il 90% delle volte se c’è un rapporto 40:60 di polsi destri rotti rispetto ai polsi sinistri. Se il rapporto tra polsi destri e sinistri è più lontano da 50:50, avrai una probabilità ancora maggiore di ottenere un risultato significativo.
Esempi
Hai intenzione di incrociare piselli che sono eterozigoti per il colore giallo/verde, dove il giallo è dominante. Il rapporto atteso nella prole è 3 giallo: 1 verde. Volete sapere se i piselli gialli sono effettivamente più o meno adatti, il che potrebbe mostrarsi come una diversa proporzione di piselli gialli rispetto al previsto. Decidete arbitrariamente che volete una dimensione del campione che rilevi una differenza significativa (P<0.05) se ci sono il 3% di piselli gialli in più o in meno del previsto, con una potenza del 90%. Verificherete i dati usando il test binomiale esatto di bontà dell’adattamento se la dimensione del campione è abbastanza piccola, o un test G di bontà dell’adattamento se la dimensione del campione è più grande. L’analisi della potenza è la stessa per entrambi i test.
Utilizzando G*Power come descritto per il test esatto di bontà dell’adattamento, il risultato è che ci vorrebbero 2109 piante di piselli se si vuole ottenere un risultato significativo (P<0.05) il 90% delle volte, se la vera proporzione di piselli gialli è 78%, e 2271 piselli se la vera proporzione è 72% giallo. Poiché sareste interessati a una deviazione in entrambe le direzioni, usate il numero più grande, 2271. Sono un sacco di piselli, ma ti rassicura vedere che non è un numero ridicolo. Se volete rilevare una differenza dello 0,1% tra il numero previsto e quello osservato di piselli gialli, potete calcolare che avrete bisogno di 1.970.142 piselli; se è questo che dovete rilevare, l’analisi della dimensione del campione vi dice che dovrete includere nel vostro budget un robot smista piselli.
I dati di esempio per il t-test a due campioni mostrano che l’altezza media nella sezione 2 p.m. di Analisi dei dati biologici era di 66,6 pollici e l’altezza media nella sezione 5 p.m. era di 64,6 pollici, ma la differenza non è significativa (P=0,207). Vuoi sapere quanti studenti dovresti campionare per avere l’80% di possibilità che una differenza così grande sia significativa. Usando G*Power come descritto nella pagina del test t a due campioni, inserite 2.0 per la differenza nelle medie. Usando la funzione STDEV in Excel, calcolate la deviazione standard per ogni campione nei dati originali; è 4.8 per il campione 1 e 3.6 per il campione 2. Inserite 0,05 per alfa e 0,80 per la potenza. Il risultato è 72, il che significa che se gli studenti delle 5 del pomeriggio fossero davvero più bassi di 5 centimetri rispetto agli studenti delle 2 del pomeriggio, avreste bisogno di 72 studenti in ogni classe per rilevare una differenza significativa l’80% delle volte, se la vera differenza è davvero di 2,0 centimetri.
Come fare analisi di potenza
G*Power
G*Power è un eccellente programma gratuito, disponibile per Mac e Windows, che farà analisi di potenza per una grande varietà di test. Spiegherò come usare G*Power per le analisi di potenza per la maggior parte dei test in questo manuale.
R
Salvatore Mangiafico’s R Companion ha programmi R di esempio per fare analisi di potenza per molti dei test in questo manuale; vai alla pagina per il singolo test e scorri in fondo per il programma di analisi di potenza.
SAS
SAS ha un PROC POWER che puoi usare per analisi di potenza. Inserisci i parametri necessari (che variano a seconda del test) e inserisci un periodo (che simboleggia i dati mancanti in SAS) per il parametro che stai risolvendo (di solito ntotal, la dimensione totale del campione, o npergroup, il numero di campioni in ogni gruppo). Trovo che G*Power sia più facile da usare rispetto a SAS per questo scopo, quindi non consiglio di usare SAS per le vostre analisi di potenza.
⇐ Precedente argomento|Successivo argomento ⇒ Indice
Questa pagina è stata rivista l’ultima volta il 20 luglio 2015. Il suo indirizzo è http://www.biostathandbook.com/power.html. Può essere citato come:
McDonald, J.H. 2014. Handbook of Biological Statistics (3rd ed.). Sparky House Publishing, Baltimora, Maryland. Questa pagina web contiene il contenuto delle pagine 40-44 della versione stampata.
©2014 di John H. McDonald. Si può probabilmente fare ciò che si vuole con questo contenuto; vedere la pagina dei permessi per i dettagli.