Darrell Henry, Louisiana State University
Nelson Eby, University of Massachusetts – Lowell
John Goodge, University of Minnesota – Duluth
David Mogk, モンタナ州立大学
結晶に一定の波長(原子スケールの結晶格子面の間隔に似ている)のX線を一定の入射角で照射すると、散乱したX線の波長が建設的に干渉して、強い反射X線が発生します。 波が建設的に干渉するためには、波の進行方向の違いが波長の整数倍になる必要がある。
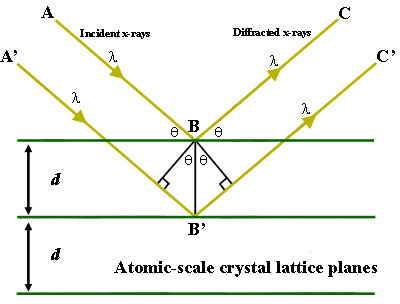
図1. ブラッグスの法則による反射。 パスABCとA’B’C’の距離が整数の波長(λ)だけ異なる場合、回折したX線は建設的な干渉を示します。
この特徴を説明するために、結晶格子の平面距離dを持つ結晶を考えます(右図)。 光線路ABCとA’B’C’の移動経路長の差が波長の整数倍である場合、その特定の波長、結晶格子平面間隔、入射角(Θ)の組み合わせで構成的干渉が起こります。 結晶中の原子の有理面は、(一定の波長のX線に対して)1つの固有の角度で屈折します。
入射X線の波長、入射角、結晶の原子の格子面の間隔の一般的な関係は、ブラッグの法則として知られており、次のように表されます:
n λ = 2d sinΘ
ここで、n(整数)は反射の「次数」、λは入射X線の波長、dは結晶の平面間の間隔、Θは入射角です。
ブラッグの法則の応用例
- X線回折(XRD)では、結晶の平面間間隔(d-spacing)を同定や特性評価の目的で使用します。 この場合、入射X線の波長は既知であり、建設的干渉が発生する入射角(Θ)を測定します。 ブラッグ方程式を解くと、建設的な干渉を起こす原子の結晶格子面間の d-spacing が得られます。 ある未知の結晶は、その構造中に多くの合理的な原子平面を持つことが予想されるため、すべての平面の「反射」を集めることで、未知の結晶を一意に特定することができます。 一般に、対称性の高い結晶(アイソメトリック系など)は、比較的少ない原子平面を持つ傾向があり、対称性の低い結晶(トリクリン系やモノクリン系)は、構造中に多数の可能性のある原子平面を持つ傾向があります。
- 波長分散型分光法(WDS)や蛍光X線分光法(XRF)の場合、分光器の分析結晶としてdスペーシングが既知の結晶を使用します。 これらのアプリケーションでは、試料と検出器の位置が固定されているため、ブラッグの法則に従って反射結晶の角度位置を変化させることで、目的の特定の波長を検出器に導き、定量的に分析することができる。 周期表のすべての元素は、K、L、Mなどの軌道「殻」の間に離散的なエネルギー差を持っており、すべての元素は一定の波長のX線を発生させる。 したがって、分光器の結晶(結晶のd間隔は固定)を使用し、結晶を独特の固定された角度(Θ)に配置することで、各元素が発する特徴的なX線の波長に基づいて、目的の元素を検出し、定量することができます。
文献
Eby, G.N., 2004, Principles of Environmental Geochemistry. Brooks/Cole-Thomson Learning, p. 212-214.
。