Heading

Nell’anno 1072 d.C., Omar Khayyam documentò la lunghezza dell’anno più precisa mai calcolata – una cifra ancora abbastanza precisa per la maggior parte degli scopi nel mondo moderno. Khayyam era un astronomo, astrologo, medico, filosofo e matematico: ha dato un contributo eccezionale all’algebra. La sua poesia è più conosciuta in Occidente di qualsiasi altro poeta non occidentale.

L’uomo stesso rimane un po’ un enigma. Diversi biografi lo hanno documentato come un agnostico amante del divertimento e bevitore di vino; uno zoroastriano nascosto; un musulmano sufi; un musulmano sunnita ortodosso; e un seguace della filosofia greca antica. Tutti concordano sul fatto che fosse un intellettuale eccezionale.

Elementi

Omar Khayyam nacque il 18 maggio 1048 nella grande città commerciale di Nishapur, nel nord della Persia. Oggi la città si trova in Iran. Il padre di Omar era Ebrahim Khayyami, un ricco medico. Il nome della madre di Omar non è noto. Alcuni autori hanno scritto che il padre di Omar si guadagnava da vivere fabbricando tende, perché Khayyami significa fabbricante di tende. Tuttavia, anche se molti anglofoni si chiamano Smith, ciò non significa che i loro padri passassero le giornate a martellare metallo caldo su un’incudine.

La famiglia di Omar era musulmana. Suo padre sembra essere stato rilassato riguardo alla religione, impiegando un matematico di nome Bahmanyar bin Marzban, un devoto dell’antica religione persiana dello Zoroastrismo, per fare da tutor a Omar. Bahmanyar era stato allievo del grande medico, scienziato e filosofo Avicenna, e diede a Omar un’educazione completa in scienza, filosofia e matematica. Khawjah al-Anbari insegnò a Omar l’astronomia, guidandolo attraverso l’Almagesto di Tolomeo.

Nella sua prima adolescenza Omar lavorò nello studio di suo padre imparando la medicina.

Omar Khayyam festeggiò il suo diciottesimo compleanno nel 1066. Nello stesso anno, la cometa di Halley apparve nel cielo, l’esercito normanno di Guglielmo il Conquistatore invase l’Inghilterra e il padre di Omar, Ebrahim, morì. Pochi mesi dopo la morte di Ebrahim, morì anche il precettore di Omar, Bahmanyar.

Era la fine di un’era nella vita di Omar Khayyam. Era tempo di mettere in ordine gli affari della sua famiglia e andare avanti.

Samarkand

Omar Khayyam si unì a una delle carovane regolari che facevano un viaggio di tre mesi da Nishapur alla grande città di Samarcanda, che ora è in Uzbekistan. Samarcanda era un centro di studi e Khayyam vi arrivò probabilmente nel 1068, all’età di 20 anni.

A Samarcanda entrò in contatto con il vecchio amico di suo padre, Abu Tahir, che era governatore e giudice capo della città. Tahir, osservando lo straordinario talento di Khayyam con i numeri, gli diede un lavoro nel suo ufficio. Presto a Khayyam fu dato un lavoro nella tesoreria del re.

Mentre viveva a Samarcanda, Khayyam fece un importante progresso nell’algebra.

I contributi di Omar Khayyam alla scienza

Algebra

Al liceo impariamo le equazioni della forma ax2 + bx + c = 0; queste sono chiamate equazioni quadratiche. Le equazioni cubiche sono della forma ax3 + bx2 + cx + d = 0. Naturalmente, le equazioni cubiche sono più difficili da risolvere delle quadratiche.

Khayyam ha congetturato correttamente che non è possibile risolvere le equazioni cubiche usando i tradizionali strumenti geometrici della Grecia antica: riga e compasso. Sono necessari altri metodi.

All’età di 22 anni, nel 1070, Khayyam pubblicò una delle sue più grandi opere: Trattato sulla dimostrazione dei problemi di algebra e bilanciamento. In esso dimostrò che un’equazione cubica può avere più di una soluzione. Mostrò anche come le intersezioni di sezioni coniche come parabole e cerchi possono essere utilizzate per ottenere soluzioni geometriche di equazioni cubiche. Archimede aveva in realtà iniziato a lavorare in questo campo più di mille anni prima, quando considerò il problema specifico di trovare il rapporto tra il volume di una parte di una sfera e un’altra. Khayyam considerò il problema in modo più generale e metodico.

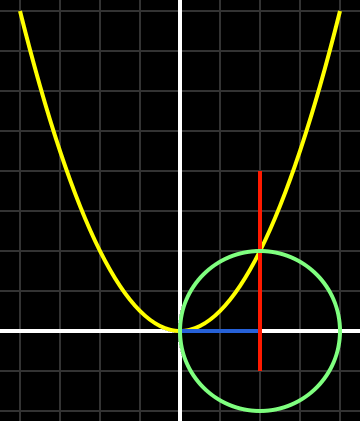
Nel linguaggio della matematica moderna, la soluzione di Khayyam all’equazione x3 + a2x = b presenta una parabola di equazione x2 = ay, un cerchio di diametro b/a2, e una linea verticale che attraversa il punto di intersezione. La soluzione è data dalla distanza sull’asse x tra l’origine e la linea verticale (rossa). Immagine di Pieter Kuiper.

Le soluzioni di Khayyam evitavano coefficienti negativi e radici negative perché i numeri negativi non erano riconosciuti nella matematica islamica. (Alcune culture, tuttavia, avevano incorporato i numeri negativi nella matematica – per esempio Brahmagupta aveva introdotto i numeri negativi nella matematica indiana 400 anni prima.)

Anche se il risultato di Khayyam fu magnifico, egli fu personalmente deluso dal fatto di dover utilizzare la geometria per risolvere le equazioni cubiche – aveva sperato di scoprire un algoritmo usando solo l’algebra.

Trattato sulla dimostrazione di problemi di algebra e bilanciamento stabilì Khayyam come un matematico di primo livello, e la sua reputazione si diffuse rapidamente in tutta la Persia.

Dopo la svolta di Khayyam ci furono pochi progressi significativi sulle equazioni cubiche fino al 1535, quando Niccolò Tartaglia trovò soluzioni generali per tutte le equazioni cubiche.

L’algebra di Khayyam non era il sistema di lettere e segni che usiamo oggi. La sua algebra era espressa in parole. Così, dove oggi scriviamo:

Solvere per x:

x2 + 6 = 5x

Khayyam scriveva: Qual è la quantità di un quadrato in modo che quando gli si aggiungono 6 dirham, diventa uguale a cinque radici di quel quadrato?

Collegare l’algebra e la geometria

Algebra e geometria furono collegate con successo da Pierre de Fermat e René Descartes nel 1600, dando origine al moderno sistema di coordinate x-y.

Il lavoro di Khayyam con le cubiche lo aveva reso certo che l’algebra e la geometria fossero collegate, e citò gli Elementi di Euclide per sostenere l’idea:

Chi pensa che l’algebra sia un trucco per ottenere incognite ha pensato invano. Non si deve prestare attenzione al fatto che l’algebra e la geometria sono diverse in apparenza. Le algebre sono fatti geometrici dimostrati dalle proposizioni 5 e 6 del libro 2 degli Elementi di Euclide.

Lunghezza dell’anno

Nel 1073, Khayyam ricevette un invito nella città persiana di Isfahan, capitale dell’impero selgiuchide, per preparare un calendario che funzionasse in modo ordinato e fosse preciso per sempre – questa era un’epoca in cui la lunghezza degli anni veniva regolarmente cambiata.

L’invito di Khayyam venne dai due uomini più potenti dell’impero selgiuchide, di cui la Persia faceva parte: si trattava di Malik Shah, sultano dell’impero, e Nizam al-Mulk, suo visir.

Khayyam reclutò altri scienziati di talento per accompagnarlo a Isfahan nel 1074. Lì ricevette uno stipendio straordinariamente alto e godette di uno stile di vita privilegiato. Malik Shah pagò Khayyam per fondare un osservatorio con l’obiettivo iniziale di fare osservazioni del cielo per 30 anni, durante i quali Saturno, il pianeta più lontano allora conosciuto, avrebbe completato un’orbita.

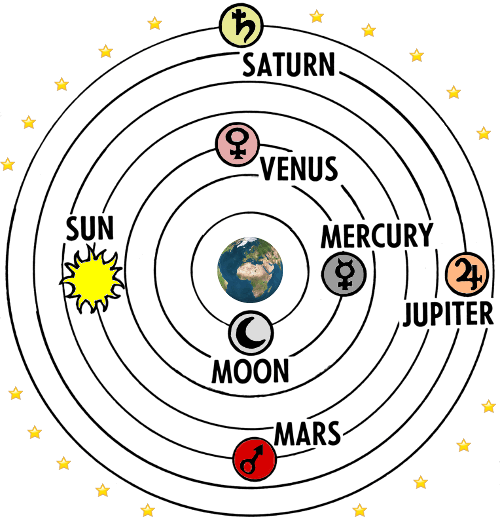
L’universo di Tolomeo – il modello accettato da Omar Khayyam.

Durante la sua permanenza a Isfahan, Khayyam misurò la lunghezza di un anno – per essere precisi la lunghezza dell’anno tropicale – con notevole accuratezza e precisione.

Khayyam trovò che 1.029.983 giorni fanno 2.820 anni. Questo dà una lunghezza dell’anno tropicale di 365,2422 giorni con sette cifre significative. Anche se è diventato di moda citare più cifre decimali di questa, l’input di Khayyam di 1.029.983 giorni contiene sette cifre significative, quindi è irragionevole citare più di questo numero di cifre significative nella lunghezza dell’anno calcolato.

Oggi sappiamo che la lunghezza di un anno tropicale cambia effettivamente di 30 minuti da un anno all’altro. La lunghezza media dell’anno tropicale citata oggi è 365,242189 giorni, che con sette cifre significative è 365,2422 giorni – esattamente la cifra a cui Khayyam arrivò quasi mille anni fa. Anche la lunghezza di un anno tropicale aumenta molto leggermente con il passare del tempo, anche se non abbastanza tra l’epoca di Khayyam e la nostra per essere evidente su una scala di sette cifre significative.

Malik Shah introdusse il nuovo calendario di Khayyam nell’Impero Selgiuchide il 15 marzo 1079. Fu usato fino al 20° secolo.

Il Postulato Parallelo

I 13 libri degli Elementi di Euclide, pubblicati nel 300 a.C. circa, furono probabilmente i libri più influenti dell’intera storia della matematica. Gli Elementi erano stati costruiti su cinque postulati geometrici – in altre parole cinque cose che si supponeva fossero vere sulla geometria: per esempio, tutti gli angoli retti sono uguali tra loro.

Il quinto dei cinque postulati di Euclide era il postulato della parallela. Il postulato delle parallele ha dimostrato di essere una fonte di perplessità, irritazione e gioia per i matematici per millenni. La gioia era di solito di breve durata, appartenente ai matematici che pensavano di aver dimostrato il postulato solo per essere delusi quando un errore veniva identificato nella loro “prova”.

Euclide aveva considerato una linea retta che attraversa altre due linee rette. Ha esaminato la situazione quando gli angoli interni (mostrati nell’immagine qui sotto) sommano meno di 180 gradi. In queste circostanze, disse che le due rette finiranno per incontrarsi sul lato dei due angoli che sommano meno di 180 gradi.

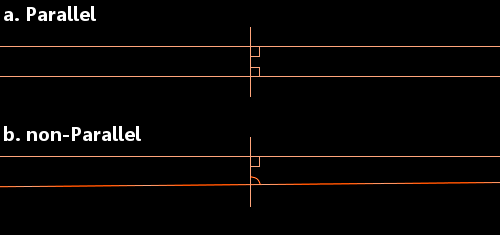
a. Quando ogni angolo è di 90 gradi, le linee sono parallele.
b. Se uno o entrambi gli angoli sono inferiori a 90 gradi, le linee si incontreranno.

Dal tempo in cui gli Elementi furono pubblicati, i matematici hanno cercato di usare i primi quattro postulati di Euclide per dimostrare il postulato della parallela. Erano destinati a fallire. Ora sappiamo che è impossibile provare il postulato della parallela usando gli altri postulati di Euclide.

Il tentativo di Omar Khayyam fu interessante. Nella sua Spiegazione delle difficoltà dei postulati negli Elementi di Euclide chiede ai suoi lettori di considerare una linea retta AB:

Chiede ai suoi lettori di considerare due linee uguali che siano perpendicolari ad AB e vede tre possibili disposizioni, che possono produrre figure a quattro lati:

"Omar Khayyam." Famous Scientists. famousscientists.org. 5 Nov. 2016. Web. <www.famousscientists.org/omar-khayyam/>.