Rozkaz króla to niezły łamigłówka
(Poziom trudności: łatwy)
Król Nupe z królestwa Catan tak bardzo kocha swoje dwie córki, że postanawia, iż w królestwie będzie lepiej, jeśli będzie więcej dziewczynek niż chłopców, i wydaje następujący dekret: Wszystkie rodzące dzieci pary muszą kontynuować rodzenie dzieci, dopóki nie urodzą córki!
Ale aby uniknąć przeludnienia, wydaje dodatkowy dekret: Wszystkie rodzące dzieci pary przestaną rodzić dzieci, gdy urodzą córkę! Jego poddani natychmiast zaczynają wykonywać jego polecenia.
Po wielu latach, jaki jest oczekiwany stosunek dziewczynek do chłopców w Catanie?
Podpowiedź
Prawdopodobieństwo, że każde urodzone dziecko będzie dziewczynką wynosi oczywiście 50 procent.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
How Many Eggs Does This Hen Lay?
(Difficulty: Easy)
Ten problem powstał na cześć mojego taty, Harolda Feivesona. To dzięki niemu uwielbiam łamigłówki matematyczne, a to jest jeden z pierwszych problemów (z wielu), które dał mi, gdy dorastałem.
Półtora kury znosi półtora jajka w ciągu półtora dnia. Ile jajek znosi jedna kura w ciągu jednego dnia?
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Złoty łańcuch to zwodniczo prosty problem matematyczny
(Poziom trudności: średni)
Grzebiesz na strychu swojej prababci, kiedy znajdujesz pięć krótkich łańcuchów, z których każdy składa się z czterech złotych ogniw. Wydaje Ci się, że gdybyś połączył je wszystkie w jedną wielką pętlę składającą się z 20 ogniw, miałbyś niesamowity naszyjnik. Więc przynosisz go do jubilera, który mówi ci, że koszt wykonania naszyjnika będzie 10 dolarów za każdy złoty link, który musi złamać, a następnie ponownie uszczelnić.
Ile to będzie kosztować?
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Try to Solve This Pickleball Puzzle
(Difficulty: 🚨HARD🚨)
Kenny, Abby i Ned zebrali się na turniej pickleballa, w którym, jak zwykle, zwycięzca zostaje po każdej grze, aby zagrać z osobą, która usiadła w tej grze. Pod koniec popołudnia Abby jest wyczerpana, po rozegraniu siedmiu ostatnich gier. Kenny, który jest mniej zmęczony, podlicza rozegrane gry:
Kenny rozegrał osiem gier
Abby rozegrała 12 gier
Ned rozegrał 14 gier
Kto wygrał czwartą grę przeciwko komu?
Podpowiedź
Ile w sumie gier zostało rozegranych?
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Nasze Zagadki Wyłącznika Obwodowego to czyste zło. Sorry.
(Difficulty: 🚨HARD🚨)
Skrzynka z wyłącznikami w Twoim nowym domu znajduje się w niewygodnym kącie piwnicy. Ku swojemu rozgoryczeniu, odkrywasz, że żaden ze 100 wyłączników nie jest oznaczony, i stajesz przed trudną perspektywą dopasowania każdego wyłącznika do jego odpowiedniego światła. (Załóżmy, że każdy wyłącznik mapuje tylko do jednego światła.)
Na początek, przełączasz wszystkie 100 świateł w domu na „on”, a następnie kierujesz się w dół do piwnicy, aby rozpocząć uciążliwy proces mapowania. Podczas każdej podróży do piwnicy możesz włączyć lub wyłączyć dowolną liczbę wyłączników. Następnie możesz przemierzać korytarze swojego domu, aby odkryć, które światła są włączone, a które wyłączone.
Jaka jest minimalna liczba podróży, które musisz odbyć do piwnicy, aby zmapować każdy wyłącznik do każdego światła?
Podpowiedź
Rozwiązanie nie wymaga ani włączania ani wyłączania włączników światła w Twoim domu ani odczuwania jak gorące są żarówki. Możesz spróbować najpierw rozwiązać zadanie dla przypadku 10 nieoznakowanych wyłączników.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Dwa pociągi. Dwie babcie. Can You Solve This Tricky Math Riddle?
(Difficulty: Moderate)
Dwie babcie Jessego chcą się z nim spotykać w każdy weekend, ale mieszkają po przeciwnych stronach miasta. W ramach kompromisu, mówi im, że w każdą niedzielę, o losowej porze dnia, uda się na stację metra najbliższą jego mieszkania i wskoczy do następnego pociągu, który przyjedzie.
Jeśli będzie to pociąg jadący na północ, odwiedzi swoją babcię Ericę w centrum miasta, a jeśli będzie to pociąg jadący na południe, odwiedzi swoją babcię Carę w centrum. Obie jego babcie są w porządku z tym planem, ponieważ wiedzą, że zarówno północne, jak i południowe pociągi kursują co 20 minut.
Ale po kilku miesiącach robienia tego, babcia Cara narzeka, że widzi go tylko w jedną z pięciu niedziel. Jesse obiecuje, że rzeczywiście udaje się na stację o przypadkowej porze każdego dnia. Jak to możliwe?
Podpowiedź
Pociągi zawsze przyjeżdżają o wyznaczonych godzinach.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Here’s a Really F@*#ing Hard Math Problem About Ants
(Difficulty: 🚨HARD🚨)
Max i Rose są mrówczym rodzeństwem. Uwielbiają się ścigać, ale zawsze remisują, ponieważ w rzeczywistości pełzają z dokładnie taką samą prędkością. Postanawiają więc stworzyć wyścig, w którym jedna z nich (miejmy nadzieję) wygra.
W tym wyścigu każda z nich zacznie w dolnym rogu prostopadłościanu, a następnie będzie czołgać się tak szybko, jak tylko potrafi, aby dotrzeć do okruchu w przeciwległym rogu. Wymiary ich prostopadłościanów są takie, jak na zdjęciu:
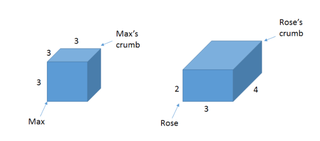
Jeśli oboje obiorą najkrótszą możliwą drogę, aby dotrzeć do swojego okruszka, kto dotrze do niego pierwszy? (Nie zapominaj, że są mrówkami, więc oczywiście mogą się wspinać w dowolnym miejscu na krawędziach lub powierzchni prostopadłościanu.)
Wskazówka
Pamiętaj: Myśl poza pudełkiem.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
This Peppermint Patty Riddle Is Practically Impossible
(Difficulty: 🚨HARD🚨)
Masz do czynienia ze swoją przyjaciółką, Caryn, w „candy-off”, który działa w następujący sposób: Jest kupka 100 karmelków i jeden peppermint patty. Ty i Caryn będą chodzić tam i z powrotem, biorąc co najmniej jeden i nie więcej niż pięć karmelków z kupki cukierków w każdej turze. Osoba, która usunie ostatni karmel, otrzyma również miętowego patty. A ty uwielbiasz miętowe patty.
Załóżmy, że Caryn pozwala ci zdecydować, kto idzie pierwszy. Kogo powinieneś wybrać, aby upewnić się, że wygrasz miętowego patty?
Podpowiedź
Najpierw rozwiąż zadanie dla stosu 10 karmelków.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Czy potrafisz rozwiązać zagadkę Wielkiej Amerykańskiej Trasy Kolejowej?
(Stopień trudności: umiarkowany)
Ten problem został zaproponowany przez fizyka P. Jeffreya Ungara.
W końcu Wielka Amerykańska Trasa Kolejowa przez cały kraj została ukończona! No dalej, poklep się po plecach – właśnie zainstalowałeś najdłuższą poręcz w historii świata, liczącą 4000 mil od początku do końca. Ale tuż po ceremonii otwarcia twój asystent przypomina ci, że metal, z którego wykonano poręcz, rozszerza się nieznacznie w lecie, więc jej długość zwiększy się w sumie o jeden cal.
„Ha!”, mówisz, „Jeden cal w poręczy o długości 4000 mil? To nic takiego!” Ale … czy masz rację?
Załóżmy, że kiedy poręcz się rozszerza, zapina się w górę w najsłabszym punkcie, który znajduje się w centrum. O ile wyżej będą musieli sięgnąć piesi w środku kraju, aby złapać się poręczy? To znaczy, na poniższym rysunku, ile wynosi h? (Dla celów tego pytania zignoruj krzywiznę Ziemi i załóż, że szlak jest linią prostą.)
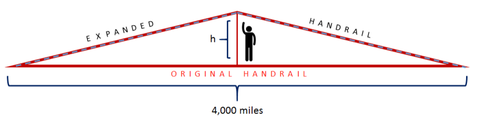
Podpowiedź
Pythagoras jest fascynującą postacią historyczną.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Ta zagadka jest jak szczególnie okrutny problem z matury. Can You Find the Answer?
(Difficulty: Moderate)
Amanda mieszka ze swoim nastoletnim synem, Mattem, na wsi – samochodem daleko od szkoły Matta. Każdego popołudnia Amanda wychodzi z domu o tej samej porze, jedzie do szkoły ze stałą prędkością, odbiera Matta dokładnie o 17:00, kiedy kończy się jego kółko szachowe, a potem razem wracają do domu z tą samą stałą prędkością. Ale pewnego dnia Matt nie czuje się dobrze, więc wcześniej opuszcza trening szachowy i zaczyna wracać do domu na przenośnej hulajnodze.
Po godzinie jazdy na hulajnodze, Amanda spotyka go w swoim samochodzie (na swojej zwykłej trasie, by go odebrać) i wracają razem, docierając do domu 40 minut wcześniej niż zwykle. Ile ćwiczeń szachowych ominęło Matta?
Podpowiedź
Rozważ przypadek, w którym Amanda spotyka Matta dokładnie w momencie, gdy wychodzi z ich domu.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Czy potrafisz przeprowadzić te 3 gwiazdy filmowe przez rzekę?
(Poziom trudności: umiarkowany)
Trzy gwiazdy filmowe, Chloe, Lexa i Jon, kręcą film w Amazonii. Są bardzo sławne i bardzo wymagające, więc ich agenci są zawsze z nimi. Pewnego dnia, po nakręceniu sceny głęboko w lesie deszczowym, trójka aktorów i ich agenci postanawiają wrócić do bazy domowej na piechotę. Nagle trafiają na dużą rzekę.
Na brzegu rzeki znajdują małą łódź wiosłową, ale jest ona wystarczająco duża, aby pomieścić dwóch z nich w jednym czasie. W czym problem? Żaden z agentów nie jest wygodny pozostawiając swoją gwiazdę filmową z innymi agentami, jeśli nie są one tam, jak również. Nie ufają, że inni agenci nie będą próbować podbierać im gwiazdę.
Na przykład, agent Chloe jest w porządku, jeśli Chloe i Lexa są same w łodzi lub na jednym z brzegów rzeki, ale zdecydowanie nie jest w porządku, jeśli agent Lexa jest również z nimi. Więc jak oni wszyscy mogą przedostać się na drugą stronę rzeki?
Podpowiedź
Nie ma tylko jednego sposobu na rozwiązanie tego problemu.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Ta potwornie trudna zagadka jest naszym hołdem dla zmarłego geniusza matematyki. Can You Figure It Out?
(Difficulty: 🚨HARD🚨)
W dniu 11 kwietnia, John Horton Conway, genialny matematyk, który miał intensywne i zabawne miłość do zagadek i gier, zmarł z powodu powikłań z COVID-19. Conway jest wynalazcą jednego z moich ulubionych legendarnych problemów (nie dla osób o słabym sercu) oraz słynnej Gry w życie. Stworzyłem ten problem na jego cześć.
Carol tworzyła drzewo genealogiczne, ale miała problemy z ustaleniem daty urodzenia swojej matki. Jedyną wskazówką, jaką znalazła, był list napisany przez jej dziadka do babci w dniu, w którym urodziła się jej matka. Niestety, niektóre znaki były rozmazane, reprezentowane tutaj przez „___”. (Długość linii nie odzwierciedla liczby rozmazanych znaków.)
„Droga Virginio,
Niewiele wiedziałem, kiedy w ten poniedziałek rano wyruszyłem do pracy, że wieczorem będziemy mieli piękną córeczkę. I to w rocznicę naszego ślubu, nie mniej! To sprawia, że wracam myślami do tego niesamowitego weekendowego dnia, 27 stycznia 19___ roku, kiedy po raz pierwszy podzieliliśmy się naszą przysięgą, że stworzymy razem rodzinę, i cóż, oto jesteśmy! Wszystkiego najlepszego z okazji ósmej rocznicy, moja miłości.
Miłość, Edwin”
Pytanie: Kiedy urodziła się matka Carol?
Podpowiedź
Ten problem jest inspirowany Regułą Zagłady Conwaya.
Rozwiązanie
Gotowi na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Aby rozwiązać tę pokrętną matematyczną zagadkę, potrzebujesz tylko jednego pasa i jednej Ziemi
(Stopień trudności: umiarkowany)
Wyobraź sobie, że masz bardzo długi pas. Cóż, bardzo długi, naprawdę … w rzeczywistości jest on wystarczająco długi, aby owinąć się wokół obwodu całej naszej planety. (Dla uproszczenia, załóżmy, że Ziemia jest idealnie okrągła, bez gór, oceanów i innych przeszkód na drodze pasa.)
Naturalnie, jesteś bardzo dumny ze swojego pasa. Ale wtedy zjawia się twój brat, Piotr, i ku twojemu niezadowoleniu pokazuje pas, który jest tylko trochę dłuższy od twojego. Przechwala się, że jego pas jest dłuższy dokładnie o jego wzrost: 6 stóp.
Jeśli Piotr miałby również owinąć swój pas wokół obwodu Ziemi, jak daleko nad powierzchnią mógłby zawiesić pas, gdyby go napiął i równomiernie rozciągnął?
Podpowiedź
Obwód Ziemi wynosi około 25 000 mil, czyli 130 milionów stóp… ale nie musisz tego wiedzieć, aby rozwiązać to zadanie.
Rozwiązanie
Gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Ta Zagadka Stukania Łokciem jest Diaboliczna. Good Luck Solving It.
(Difficulty: 🚨HARD🚨)
W pewnym czasie w przyszłości, gdy schronienie w miejscu zakazy są zniesione, małżeństwo, Florian i Julia, głowa nad do baru, aby świętować ich nowo odkrytą wolność.
Znajdują tam cztery inne pary, które wpadły na ten sam pomysł.
Chcąc nawiązać kontakt towarzyski, każda osoba z pięciu par entuzjastycznie stuka się łokciami (nowy uścisk dłoni) z każdą osobą, której jeszcze nie spotkała.
Właściwie okazuje się, że wiele z tych osób znało się już wcześniej, więc kiedy Julia pyta wszystkich, ile łokci każdy z nich stuknął, otrzymuje dziewięć różnych odpowiedzi!
Pytanie: Ile łokci stuknął Florian?
Podpowiedź
Jakie dziewięć odpowiedzi usłyszała Julia?
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
You’ll Need a Drink After Trying to Solve This Whisky Riddle
(Difficulty: Easy)
Alan i Claire żyją zgodnie ze starym szkockim powiedzeniem: „Nigdy nie miej whisky bez wody, ani wody bez whisky!”. Więc pewnego dnia, kiedy Alan ma przed sobą szklankę whisky, a Claire ma przed sobą tej samej wielkości szklankę wody, Alan bierze łyżkę swojej whisky i wlewa ją do wody Claire.
Claire miesza swoją zabarwioną whisky wodę, a następnie wlewa łyżkę tej mieszanki z powrotem do whisky Alana, aby upewnić się, że mają dokładnie tyle samo do wypicia.
A więc: Czy więcej jest wody w whisky Alana, czy więcej whisky w wodzie Claire? I czy to ma znaczenie jak dobrze Claire mieszała?
Podpowiedź
Rozmiar łyżki nie ma znaczenia.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić czy masz rację.
Problem z bazgrołami jest o wiele trudniejszy niż się wydaje. Czy potrafisz go rozwiązać?
(Stopień trudności: umiarkowany)
Zagadka z tego tygodnia jest stosunkowo prosta, ale jednocześnie złowieszcza.
Pytanie: Czy można utworzyć liczbę 100, przeplatając dowolną liczbę plusów i minusów w ciągu cyfr 9 8 7 6 5 4 3 2 1? Nie można zmienić kolejności cyfr! Jaka jest więc najmniejsza liczba plusów i minusów potrzebna do utworzenia liczby 100?
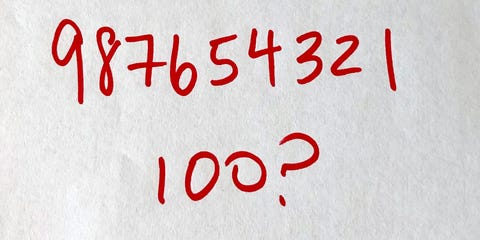
Na przykład 98 – 7 – 6 + 54 – 32 pokazuje jeden sposób przeplatania plusów i minusów, ale ponieważ równa się on 107, nie jest rozwiązaniem.
Nazywam to „problemem bazgrołów”: taki, nad którym najlepiej pracować podczas spotkań, gdzie w przeciwnym razie mógłbyś bazgrać.
Podpowiedź
Możesz zacząć szukać rozwiązań, które używają w sumie siedmiu plusów i minusów (chociaż są sposoby, aby użyć mniej).
Rozwiązanie
Gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Ta matematyczna łamigłówka zaskoczyła każdego naukowca oprócz jednego. Think You Can Crack It?
(Difficulty: HARD)
W hołdzie Freemanowi Dysonowi, znanemu fizykowi, który zmarł w zeszłym miesiącu, oto legendarna opowieść demonstrująca jego błyskotliwy dowcip i niesamowitą moc umysłu.
Pewnego dnia, podczas spotkania najlepszych naukowców, jeden z nich zastanawiał się głośno, czy istnieje liczba całkowita, którą można dokładnie podwoić, przesuwając jej ostatnią cyfrę na przód. Na przykład 265 spełniałoby to warunek, gdyby 526 było jej dokładnym podwojeniem – a tak nie jest.
Po pozornie zaledwie pięciu sekundach Dyson odpowiedział: „Oczywiście, że istnieje, ale najmniejsza taka liczba ma 18 cyfr.”
To pozostawiło niektórych z najmądrzejszych naukowców na świecie zastanawiających się nad tym, jak mógł to rozgryźć tak szybko.
Więc biorąc pod uwagę podpowiedź Dysona, jaka jest najmniejsza taka liczba?
Podpowiedź
Mój drugoklasista nauczył się ostatnio dodawać do siebie trzycyfrową liczbę za pomocą klasycznej metody pionowej:

18-cyfrowe liczby, oczywiście, można dodawać w ten sam sposób.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Dowiedz się, co jest na jej czole
(Trudność: Umiarkowana)
Cecylia uwielbia testować logikę swoich bardzo logicznych przyjaciół: Jayi, Juliana i Leviego, więc ogłasza:
„Napiszę dodatnią liczbę na każdym z waszych czół. Żadna z tych liczb nie jest taka sama, a dwie z nich dodają się do trzeciej.”
Naznacza liczby na ich czołach, po czym zwraca się do Jayi i pyta ją, jaka jest jej liczba. Jaya widzi, że Julian ma 20 na czole, a Levi ma 30 na swoim. Ona myśli przez chwilę, a następnie mówi: „Nie wiem, co mój numer jest”. Julian wtrąca: „Ja też nie znam swojego numeru”, a potem Levi krzyczy: „Ja też nie!”. Cecilia radośnie mówi: „W końcu udało mi się was pokonać!”.
„Nie tak szybko!” mówi Jaya. „Teraz znam swój numer!”
Jaki jest numer Jayi?
Podpowiedź
Jaya może być jednym z dwóch numerów, ale tylko jeden z tych numerów doprowadziłby do tego, że Julian i Levi obaj nie znaliby swoich numerów. Dlaczego?
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Czy Keanu Reeves może zostać wybrany na prezydenta?
(Stopień trudności: umiarkowany)
Jest rok 2024, a w demokratycznych prawyborach startuje pięciu kandydatów: Taylor Swift, Oprah Winfrey, Mark Cuban, Keanu Reeves i Dwayne Johnson. (Hej, to może się zdarzyć.) Jak zwykle, pierwsze prawybory są w Iowa.
W dążeniu do przezwyciężenia zażenowania po klęsce „caucus 2020”, Partia Demokratyczna Iowa ogłosiła właśnie nowy, niezawodny sposób na wyłonienie najlepszego kandydata: odbędą się cztery kolejne wybory.
Najpierw kandydat nr 1 wystartuje przeciwko kandydatowi nr 2. Następnie zwycięzca tego pojedynku zmierzy się z kandydatem nr 3, potem ten sam zwycięzca zmierzy się z kandydatem nr 4, a na koniec zwycięzca tych wyborów zmierzy się z ostatnim kandydatem. Zgodnie z zasadą przechodniości, zwycięzca tych ostatnich wyborów musi być najlepszym kandydatem… tak twierdzi Partia Demokratyczna Iowa.
Kandydat Keanu czuje się dość nisko, ponieważ wie, że przez większość wyborców jest klasyfikowany na samym dole, a przez nikogo nie jest na szczycie. W rzeczywistości wie, że populacja Iowa jest podzielona na pięć równych grup, a ich preferencje są następujące:

Kandydat Keanu czuje się dość słabo.
Keanu jest przyjacielem z dzieciństwa z Bill S. Preston, Esq…, nowym szefem Partii Demokratycznej w Iowa. Preston, pewny, że kolejność kandydatów nie ma znaczenia dla wyniku, mówi Keanu, że może wybrać kolejność głosowania kandydatów.
Jaką więc kolejność powinien wybrać Keanu?
Podpowiedź
Jak Keanu poradziłby sobie w wyścigach jeden na jeden z każdym kandydatem?
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.
Kto otworzył te wszystkie cholerne szafki?
(Poziom trudności: średni)
W głównym korytarzu Liceum w Chełmie znajduje się 100 szafek. Każdej nocy dyrektor szkoły upewnia się, że wszystkie szafki są zamknięte, aby zapewnić porządek na początku następnego dnia. Pewnego dnia 100 złośliwych uczniów postanawia, że zrobi im psikusa.
Uczniowie spotykają się przed rozpoczęciem lekcji i ustawiają się w szeregu. Pierwszy uczeń idzie korytarzem i otwiera każdą szafkę. Następny uczeń podąża zamykając każdą inną szafkę (zaczynając od drugiej szafki). Uczeń 3 następnie idzie do każdej trzeciej szafki (zaczynając od trzeciej) i otwiera ją, jeśli jest zamknięta, i zamyka, jeśli jest otwarta. Uczeń 4 podąża za nim, otwierając co czwartą szafkę, jeśli jest zamknięta i zamykając ją, jeśli jest otwarta. I tak w kółko, aż w końcu uczeń 100 idzie do setnej szafki. Kiedy dyrektor przyjdzie później rano, które szafki zastanie otwarte?
Podpowiedź
Upewnij się, że zwracasz uwagę na wszystkie czynniki.
Rozwiązanie
Czy jesteś gotowy na rozwiązanie? Kliknij tutaj, aby sprawdzić, czy masz rację.