Darrell Henry, Louisiana State University
Nelson Eby, University of Massachusetts – Lowell
John Goodge, University of Minnesota – Duluth
David Mogk, Montana State University
Gdy kryształ jest bombardowany promieniami X o stałej długości fali (podobnej do rozstawu płaszczyzn sieci krystalicznej w skali atomowej) i pod pewnym kątem padania, intensywne odbite promienie X są produkowane, gdy długości fal rozproszonych promieni X interferują konstruktywnie. Aby fale interferowały konstruktywnie, różnice w drodze podróży muszą być równe całkowitym wielokrotnościom długości fali. Kiedy taka konstruktywna interferencja zachodzi, dyfraktowana wiązka promieniowania X opuści kryształ pod kątem równym kątowi wiązki padającej.
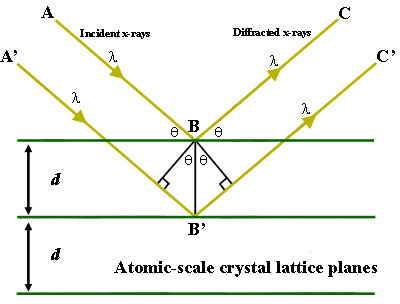
Rysunek 1. Odbicie zgodnie z prawem Bragga. Dyfraktowane promienie X wykazują interferencję konstruktywną, gdy odległość między ścieżkami ABC i A’B’C' różni się o całkowitą liczbę długości fali (λ).
Aby zilustrować tę cechę, rozważmy kryształ o odległościach planarnych sieci krystalicznej d (po prawej). Tam, gdzie różnica długości drogi podróży między ścieżkami promieni ABC i A’B’C' jest całkowitą wielokrotnością długości fali, interferencja konstruktywna wystąpi dla kombinacji tej konkretnej długości fali, odstępu między płaszczyznami sieci krystalicznej i kąta padania (Θ). Każda racjonalna płaszczyzna atomów w krysztale ulegnie załamaniu pod jednym, niepowtarzalnym kątem (dla promieniowania rentgenowskiego o stałej długości fali).
Ogólna zależność między długością fali padającego promieniowania X, kątem padania i odstępem między płaszczyznami atomów w krysztale jest znana jako prawo Bragga, wyrażone jako:
n λ = 2d sinΘ
gdzie n (liczba całkowita) jest „rzędem” odbicia, λ jest długością fali padającego promieniowania X, d jest odstępem międzypłaszczyznowym kryształu, a Θ jest kątem padania.
Zastosowania prawa Bragga.
- W dyfrakcji rentgenowskiej (XRD) odstępy międzypłaszczyznowe (d-spacing) kryształu są wykorzystywane do celów identyfikacji i charakterystyki. W tym przypadku znana jest długość fali padającego promieniowania rentgenowskiego i mierzony jest kąt padania (Θ), przy którym zachodzi interferencja konstruktywna. Rozwiązując równanie Bragga otrzymuje się odległość d pomiędzy płaszczyznami sieci krystalicznej atomów, które powodują interferencję konstruktywną. Oczekuje się, że dany nieznany kryształ będzie posiadał w swojej strukturze wiele racjonalnych płaszczyzn atomów; dlatego zbiór „odbić” wszystkich płaszczyzn może być użyty do jednoznacznej identyfikacji nieznanego kryształu. Ogólnie rzecz biorąc, kryształy o wysokiej symetrii (np. układ izometryczny) mają tendencję do posiadania stosunkowo niewielu płaszczyzn atomowych, podczas gdy kryształy o niskiej symetrii (w układach triclinic lub monoklinic) mają tendencję do posiadania dużej liczby możliwych płaszczyzn atomowych w ich strukturach.
- W przypadku spektrometrii dyspersyjnej długości fali (WDS) lub spektroskopii fluorescencji rentgenowskiej (XRF), kryształy o znanych d-spacings są używane jako kryształy analizujące w spektrometrze. Ponieważ w tych zastosowaniach położenie próbki i detektora jest stałe, położenie kątowe kryształu odbijającego zmienia się zgodnie z prawem Bragga, tak aby interesująca nas długość fali mogła być skierowana do detektora w celu analizy ilościowej. Każdy pierwiastek w Układzie Okresowym posiada dyskretną różnicę energii pomiędzy orbitalnymi „powłokami” (np. K, L, M), tak że każdy pierwiastek będzie wytwarzał promieniowanie rentgenowskie o stałej długości fali. Dlatego też, używając kryształu spektrometru (z ustalonym odstępem d kryształu) i ustawiając kryształ pod unikalnym i stałym kątem (Θ), możliwe jest wykrycie i określenie ilościowe interesujących nas pierwiastków w oparciu o charakterystyczne długości fal rentgenowskich wytwarzanych przez każdy pierwiastek.
Literatura
Eby, G.N., 2004, Principles of Environmental Geochemistry. Brooks/Cole-Thomson Learning, s. 212-214.