Heading

br>

As ordens do Rei Fazem por um Inferno de Cérebros Teaser

(Dificuldade: Fácil)
>/p>p>King Nupe do reino Catan dotes nas suas duas filhas tanto que decide que o reino ficaria melhor com mais raparigas do que rapazes, e faz o seguinte decreto: Todos os casais com filhos devem continuar a ter filhos até terem uma filha!

mas para evitar a superpopulação, ele faz um decreto adicional: Todos os casais que tenham filhos deixarão de ter filhos quando tiverem uma filha! Os seus súbditos começam imediatamente a seguir as suas ordens.

Após muitos anos, qual é a proporção esperada de raparigas para rapazes em Catan?

Dica

A probabilidade de cada bebé nascido ser uma rapariga é, evidentemente, de 50%.

Solução

Pronto para a solução? Clique aqui para ver se tem razão.

Quantos ovos esta galinha põe?

(Dificuldade: Fácil)

Este problema é em honra do meu pai, Harold Feiveson. É devido a ele que adoro puzzles matemáticos, e este é um dos primeiros problemas (de muitos) que ele me deu quando eu estava a crescer.

Uma galinha e meia põe um ovo e meio num dia e meio. Quantos ovos é que uma galinha põe num dia?

Solução

Pronto para a solução? Clique aqui para ver se está certo.

O problema da Corrente de Ouro Matemática é Deceptivamente Simples

(Dificuldade: Moderado)

Estás a rondar o sótão da tua bisavó quando encontras cinco cadeias curtas, cada uma feita de quatro elos de ouro. Ocorre-lhe que se as combinasse todas num grande laço de 20 elos, teria um colar incrível. Então, trazem-no para um joalheiro, que vos diz que o custo de fazer o colar será de 10 dólares por cada elo de ouro que ela tem de quebrar e depois voltar a selar.

Quanto custará?

Solução

Pronto para a solução? Clique aqui para ver se está certo.

Tente resolver este puzzle de pickles

(Dificuldade: 🚨HARD🚨)

Kenny, Abby, e Ned juntaram-se para um torneio de pickles de pickles, onde, como de costume, o vencedor permanece depois de cada jogo para jogar com a pessoa que se sentava fora desse jogo. No final da sua tarde de pickleball, Abby está exausta, tendo jogado os últimos sete jogos seguidos. Kenny, que está menos cansado, conta os jogos jogados:

Kenny jogou oito jogos

Abby jogou 12 jogos

Ned jogou 14 jogos

Quem ganhou o quarto jogo contra quem?

P> Dica

Quantos jogos no total foram jogados?

Solução

Pronto para a solução? Clique aqui para ver se tem razão.

O nosso Enigma Disjuntor é Puro Maligno. Desculpe.

(Dificuldade: 🚨HARD🚨)

A caixa do disjuntor na sua nova casa está num canto inconveniente da sua cave. Para seu desgosto, descobre que nenhum dos 100 disjuntores está etiquetado, e enfrenta a perspectiva assustadora de combinar cada disjuntor com a sua respectiva luz. (Suponha que cada disjuntor mapeia apenas uma luz.)

Para começar, muda todas as 100 luzes da casa para “on”, e depois dirige-se à sua cave para iniciar o oneroso processo de mapeamento. Em cada viagem até à sua cave, pode ligar ou desligar qualquer número de disjuntores. Pode então percorrer os corredores da sua casa para descobrir que luzes estão ligadas e quais estão desligadas.

Qual é o número mínimo de viagens que precisa de fazer à cave para mapear cada disjuntor a cada luz?

P> Dica

A solução não implica ligar ou desligar os interruptores de luz em sua casa ou sentir o calor das lâmpadas. Talvez queira tentar resolver primeiro o caso de 10 disjuntores não rotulados.

Solução

Pronto para a solução? Clique aqui para ver se está certo.

Dois Comboios. Dois Grandmas. Consegue resolver este enigma matemático complicado?

(Dificuldade: Moderado)

As duas avós de Jesse querem vê-lo todos os fins-de-semana, mas vivem em lados opostos da cidade. Como compromisso, ele diz-lhes que todos os domingos, ele irá para a estação de metro mais próxima do seu apartamento a uma hora aleatória do dia e apanhará o próximo comboio que chegar.

Se por acaso for o comboio que viaja para norte, ele irá visitar a sua avó Erica no centro da cidade, e se por acaso for o comboio que viaja para sul, ele irá visitar a sua avó Cara no centro da cidade. Ambas as avós estão de acordo com este plano, uma vez que sabem que tanto os comboios que viajam para norte como para sul circulam a cada 20 minutos.

Mas depois de alguns meses a fazer isto, a avó Cara queixa-se de que o vê apenas um em cada cinco domingos. Jesse promete que se dirige à estação a uma hora aleatória todos os dias. Como pode isto ser?

P> Dica

Os comboios chegam sempre às horas programadas.

Solução

Pronto para a solução? Clique aqui para ver se tem razão.

Aqui está um Problema de Matemática Difícil sobre formigas

(Dificuldade: 🚨HARD🚨)

Max e Rose são irmãos formigas. Adoram correr uma com a outra, mas empatam sempre, uma vez que na realidade rastejam exactamente à mesma velocidade. Assim, decidem criar uma corrida em que um deles (esperançosamente) vencerá.

Para esta corrida, cada um deles começará no canto inferior de um cubóide, e depois rastejará o mais rápido que puder para chegar a uma migalha no canto oposto. As medidas dos seus cubóides são as que estão ilustradas:

Laura Feiveson

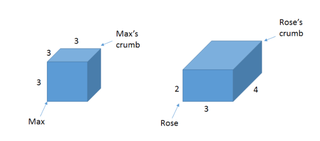
Se ambos tomarem o caminho mais curto possível para chegar à sua migalha, quem chegará primeiro à sua migalha? (Não se esqueça que são formigas, por isso é claro que podem escalar em qualquer lugar nas bordas ou superfície do cubóide.)

P>P>Dica

Remmbrar: Pense fora da caixa.

Solução

Pronto para a solução? Clique aqui para ver se está certo.

Esta Adivinha de Hortelã Pimenta é Praticamente Impossível

(Dificuldade: 🚨HARD🚨)

Estás de frente para a tua amiga, Caryn, num “doce-off”, que funciona como se segue: Há uma pilha de 100 caramelos e um caramelo de hortelã-pimenta. Você e Caryn vão e vêm tirando pelo menos um e não mais de cinco caramelos da pilha de caramelos em cada volta. A pessoa que remover o último caramelo também receberá o doce de hortelã-pimenta. E adora as pastilhas de hortelã-pimenta.

Posicionar Caryn deixa-o decidir quem vai primeiro. Quem deve escolher para se certificar de que ganha o bolo de hortelã-pimenta?

P>P>Primeiro, resolver para uma pilha de 10 caramelos.

Solução

Pronto para a solução? Clique aqui para ver se está certo.

Pode resolver o Grande Enigma Ferroviário Americano?

(Dificuldade: Moderado)

Este problema foi sugerido pelo físico P. Jeffrey Ungar.

Finalmente, o Grande Enigma Ferroviário Americano está completo em todo o país! Vá em frente, dê uma palmadinha nas costas – acabou de instalar o corrimão mais longo da história do mundo, com 4.000 milhas do princípio ao fim. Mas logo após a cerimónia de abertura, o seu assistente lembra-lhe que o metal que utilizou para o corrimão se expande ligeiramente no Verão, de modo que o seu comprimento aumentará um centímetro no total.

“Ha!” diz você, “Uma polegada num corrimão de 4.000 milhas? Isso não é nada!” Mas … tem razão?

P>Suponhamos que quando o corrimão se expande, ele se dobra para cima no seu ponto mais fraco, que está no centro. Quanto mais alto terão os peões no meio do país de chegar no Verão para agarrar o corrimão? Isto é, na figura abaixo, o que é h? (Para efeitos desta pergunta, ignorar a curvatura da Terra e assumir que o trilho é uma linha recta.)

Laura Feiveson

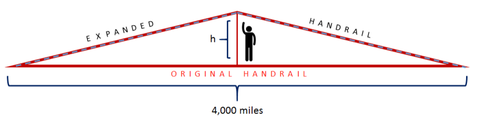
Pi>Pythagoras é uma figura histórica fascinante.

Solução

Pronto para a solução? Clique aqui para ver se está certo.

Esta Adivinha é como um Problema Especialmente Cruel do SAT. Consegue encontrar a resposta?

(Dificuldade: Moderado)

Amanda vive com o seu filho adolescente, Matt, no campo – uma viagem de carro para longe da escola de Matt. Todas as tardes, Amanda sai de casa ao mesmo tempo, conduz até à escola a uma velocidade constante, pega no Matt exactamente quando o seu clube de xadrez termina às 17 horas, e depois regressam imediatamente juntos a casa à mesma velocidade constante. Mas um dia, Matt não se sente bem, por isso deixa o treino de xadrez cedo e começa a ir para casa na sua scooter portátil.

Depois de Matt ter estado a andar de scooter durante uma hora, Amanda depara-se com ele no seu carro (na sua rota habitual para o ir buscar), e eles regressam juntos, chegando a casa 40 minutos mais cedo do que costumam fazer. Quanta prática de xadrez faltou a Matt?

P>P>Considerar o caso em que Amanda encontra Matt exactamente quando está a sair de casa deles.

Solução

Pronto para a solução? Clique aqui para ver se está certo.

P>Pode obter estas 3 estrelas de cinema do outro lado do rio?

(Dificuldade: Moderado)

Três estrelas de cinema, Chloe, Lexa, e Jon, estão a filmar um filme na Amazónia. São muito famosos e de muito alta manutenção, por isso os seus agentes estão sempre com eles. Um dia, após filmarem uma cena nas profundezas da floresta tropical, os três actores e os seus agentes decidem voltar para casa a pé. De repente, chegam a um grande rio.

Nas margens do rio, encontram um pequeno barco a remos, mas só é suficientemente grande para segurar dois deles de cada vez. A captura? Nenhum dos agentes se sente confortável em deixar a sua estrela de cinema com quaisquer outros agentes se não estiverem lá também. Eles não confiam que os outros agentes não tentem caçar a sua estrela.

Por exemplo, o agente da Chloe está bem se a Chloe e a Lexa estiverem sozinhas no barco ou numa das margens do rio, mas definitivamente não está bem se o agente da Lexa também estiver com eles. Então, como podem todas atravessar o rio?

P>P>Não há apenas uma maneira de resolver este problema.

Solução

Pronto para a solução? Clique aqui para ver se tem razão.

Esta Adivinha Rudiosamente Difícil é a nossa homenagem a um génio da matemática tardia. Consegue perceber?

(Dificuldade: 🚨HARD🚨)

A 11 de Abril, John Horton Conway, um matemático brilhante que tinha um amor intenso e lúdico por puzzles e jogos, morreu de complicações da COVID-19. Conway é o inventor de um dos meus problemas lendários favoritos (não para os fracos de coração) e, famoso, o Jogo da Vida. Eu criei este problema em sua honra.

Carol estava a criar uma árvore genealógica, mas tinha dificuldade em localizar a data de nascimento da sua mãe. A única pista que encontrou foi uma carta escrita pelo seu avô à sua avó no dia do nascimento da sua mãe. Infelizmente, algumas das personagens foram manchadas, representadas aqui com um “___”. (O comprimento da linha não reflecte o número de caracteres manchados.)

“Querida Virginia,

P>A mínima que eu sabia quando me dirigi ao trabalho esta segunda-feira de manhã, que à noite teríamos uma linda menina. E no nosso aniversário de casamento, nada menos! Faz-me pensar naquele incrível dia de fim-de-semana, J___ 27, 19___, quando partilhámos pela primeira vez o nosso voto de criar uma família juntos, e, bem, aqui estamos nós! Feliz oitavo aniversário, meu amor.

p>Amor, Edwin”p>A pergunta: Quando nasceu a mãe de Carol?

P> Dica

Este problema é inspirado pela Regra do Juízo Final de Conway.

Solução

Pronto para a solução? Clique aqui para ver se está certo.

Para resolver este Enigma Matemático Tortuoso, Basta um cinto e uma terra

(Dificuldade: Moderada)

P>Imagine que tem um cinto muito comprido. Bem, extremamente longo, realmente… de facto, é apenas suficientemente longo para se poder enrolar confortavelmente à volta da circunferência de todo o nosso planeta. (Para simplificar, suponhamos que a Terra é perfeitamente redonda, sem montanhas, oceanos, ou outras barreiras no caminho do cinto.)

Naturalmente, está muito orgulhoso do seu cinto. Mas depois o seu irmão, Peter, aparece – e para seu descontentamento, ele produz um cinto que é apenas um pouco mais longo do que o seu. Ele gaba-se de que o seu cinto é mais comprido exactamente pela sua altura: 2,5 metros.

Se Peter também enrolasse o seu cinto à volta da circunferência da Terra, quão acima da superfície poderia ele suspender o cinto se o puxasse de forma tensa e uniforme?

Dica

A circunferência da Terra é de cerca de 25.000 milhas, ou 130 milhões de pés … mas não precisa de saber isso para resolver este problema.

Solução

Pronto para a solução? Clique aqui para ver se tem razão.

Esta Adivinha de Cotovelo é Diabólica. Good Luck Solving It.

(Dificuldade: 🚨HARD🚨)

Em algum tempo futuro, quando as proibições de abrigo no local forem levantadas, um casal, Florian e Julia, dirigir-se-ão a um bar para celebrar a sua nova liberdade.

Encontram lá outros quatro casais que tiveram a mesma ideia.

Ansiosos por contacto social, cada pessoa dos cinco casais bate com entusiasmo nos cotovelos (o novo aperto de mão) com cada pessoa que ainda não conheceram.

Acontece que muitas das pessoas já se tinham conhecido antes, por isso quando Julia pergunta a todos quantos cotovelos cada um tocou, ela obtém notavelmente nove respostas diferentes!

A pergunta: Quantos cotovelos é que Florian bateu?

Dica

Que nove respostas ouviu Júlia?

Solução

Pronta para a solução? Clique aqui para ver se tem razão.

Necessitará de uma bebida depois de tentar resolver este Whisky Riddle

(Dificuldade: Fácil)
>/p>p>Alan e Claire vivem pelo velho ditado escocês: “Nunca beba whisky sem água, nem água sem whisky!” Assim, um dia, quando Alan tem à sua frente um copo de whisky, e Claire tem à sua frente um copo de água do mesmo tamanho, Alan pega numa colher do seu whisky e coloca-a na água de Claire.
Claire agita a sua água com whisky, e depois coloca uma colher desta mistura de volta no whisky de Alan para se certificar de que eles têm exactamente a mesma quantidade para beber.

Então: Há mais água no whisky de Alan, ou mais whisky na água de Claire? E importa quão bem Claire se mexeu?

Dica

O tamanho da colher não importa.

Solução

Pronto para a solução? Clique aqui para ver se está certo.

O problema do Doodle é muito mais difícil do que parece. Conseguirá resolvê-lo?

(Dificuldade: Moderado)

O enigma desta semana é relativamente simples – mas sinistro na mesma.

A pergunta: Consegue-se fazer 100, intercalando qualquer número de prós e contras dentro da cadeia de dígitos 9 8 7 6 5 4 3 2 1? Não se pode alterar a ordem dos dígitos! Então qual é o menor número de prós e contras necessário para fazer 100?

Andrew Daniels

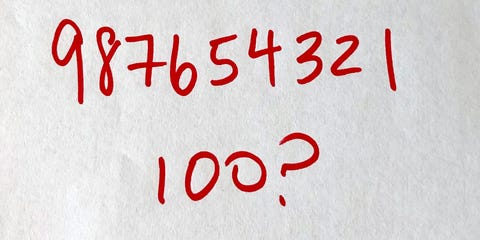
Por exemplo, 98 – 7 – 6 + 54 – 32 mostra uma forma de entrelaçar os prós e os contras, mas como é igual a 107, não é uma solução.

Chamo a isto um “problema de rabiscos”: um que é melhor trabalhado durante as reuniões em que poderia estar a rabiscar de outra forma.

Dica

Talvez queira começar a procurar soluções que utilizem um total de sete prós e contras (embora haja formas de utilizar menos).

Solução

Pronto para a solução? Clique aqui para ver se está certo.

Este Enigma Matemático Empolgou Todos os Cientistas menos Um. Think You Can Crack It?

(Dificuldade: HARD)

Em honra de Freeman Dyson, o famoso físico que morreu no mês passado, aqui está um conto lendário demonstrando a sua rapidez e incrível poder cerebral.

Um dia, numa reunião de cientistas de topo, um deles perguntou-se em voz alta se existe um número inteiro que poderia exactamente duplicar movendo o seu último dígito para a sua frente. Por exemplo, 265 satisfaria isto se 526 fosse o seu duplo exacto – o que não é.

Após aparentemente apenas cinco segundos, Dyson respondeu: “Claro que existe, mas o mais pequeno desses números tem 18 dígitos”.

Este facto deixou alguns dos cientistas mais inteligentes do mundo a pensar como poderia ele ter descoberto isto tão rapidamente.

Então, dada a dica de Dyson, qual é o número mais pequeno de tal forma?

P>P>O meu aluno do segundo ano aprendeu recentemente como adicionar um número de 3 dígitos a si próprio, utilizando o método vertical clássico:

Andrew Daniels

números de 18 dígitos, claro, podem ser adicionados da mesma forma.

Solução

Pronto para a solução? Clique aqui para ver se tem razão.

Figura para fora O que está na Testa dela

(Dificuldade: Moderado)

Cecilia adora testar a lógica dos seus amigos muito lógicos Jaya, Julian, e Levi, por isso ela anuncia:

“Vou escrever um número positivo em cada uma das suas testas. Nenhum dos números é igual, e dois dos números somam-se ao terceiro.”

Ela rabisca os números nas suas cabeças, depois vira-se para Jaya e pergunta-lhe qual é o seu número. Jaya vê Julian tem 20 na sua testa, e Levi tem 30 na sua. Ela pensa por um momento e depois diz: “Eu não sei qual é o meu número”. Julian cachimbo dentro, “Eu também não sei o meu número”, e depois Levi exclama, “Eu também não”! Cecilia regozija-se e diz: “Finalmente, surpreendi-vos!”

“Não tão depressa!” diz Jaya. “Agora eu sei o meu número!”

Qual é o número de Jaya?

P>P>Jaya poderia ser um de dois números, mas apenas um desses números levaria a que Julian e Levi não soubessem ambos os seus números. Porquê?

Solução

Pronto para a solução? Clique aqui para ver se tem razão.

Pode Keanu Reeves ser eleito como Presidente?

(Dificuldade: Moderado)

É 2024, e há cinco candidatos a concorrer nas primárias democráticas: Taylor Swift, Oprah Winfrey, Mark Cuban, Keanu Reeves, e Dwayne Johnson. (Ei, pode acontecer.) Como de costume, a primeira primária é em Iowa.

Num esforço para ultrapassar o seu embaraço após o fracasso do caucus de 2020, o Partido Democrático de Iowa acaba de anunciar uma nova e infalível forma de encontrar o melhor candidato: haverá quatro eleições consecutivas.

P>Primeiro, o candidato 1 irá concorrer contra o candidato 2. A seguir, o vencedor dessa eleição concorrerá contra o candidato 3, depois esse vencedor concorrerá contra o candidato 4, e finalmente o vencedor dessa eleição concorrerá contra o candidato final. Pela propriedade transitória, o vencedor desta última eleição deve ser o melhor candidato … assim diz o Partido Democrático de Iowa.

Candidato Keanu tem estado a sentir-se bastante em baixo, pois sabe que está classificado perto da base pela maioria dos eleitores, e no topo por nenhum. De facto, ele sabe que a população de Iowa está dividida em cinco grupos iguais, e que as suas preferências são as seguintes:

.

Keanu é amigo de infância de Bill S. Preston, Esq.., o novo chefe do Partido Democrático de Iowa. Preston, confiante de que a ordem dos candidatos não importa para o resultado, diz a Keanu que pode escolher a ordem de votação dos candidatos.

Então que ordem deve Keanu escolher?

Dica

Como se sairia Keanu em corridas individuais contra cada candidato?

Solução

Preston, confiante de que a ordem dos candidatos não importa para o resultado, diz a Keanu que pode escolher a ordem de votação dos candidatos. Clique aqui para ver se está certo.

Quem abriu todos estes malditos cacifos?

(Dificuldade: Moderado)

Existem 100 cacifos que alinham o corredor principal da Chelm High School. Todas as noites, o director da escola certifica-se de que todos os cacifos estão fechados para que haja um início ordeiro até ao dia seguinte. Um dia, 100 alunos maliciosos decidem que vão pregar uma partida.

Os alunos encontram-se todos antes do início das aulas e fazem fila. O primeiro aluno caminha então pelo corredor, e abre todos os cacifos. O aluno seguinte segue fechando todos os outros cacifos (começando no segundo cacifo). O aluno 3 vai então a cada terceiro cacifo (começando pelo terceiro) e abre-o se estiver fechado, e fecha-o se estiver aberto. O aluno 4 segue abrindo cada quarto cacifo, se estiver fechado, e fechando-o, se estiver aberto. Isto continua e continua até ao centésimo cacifo do Student 100. Quando a directora chega mais tarde de manhã, que cacifos encontra abertos?

Hint

Cuidado de prestar atenção a todos os factores.

Solução

Pronto para a solução? Clique aqui para ver se tem razão.