p>Darrell Henry, Louisiana State University
Nelson Eby, University of Massachusetts – Lowell
John Goodge, University of Minnesota – Duluth
David Mogk, Montana State University
Quando um cristal é bombardeado com raios X de um comprimento de onda fixo (semelhante ao espaçamento dos planos de grelha de cristal à escala atómica) e em certos ângulos de incidência, são produzidos raios X reflectidos intensos quando os comprimentos de onda dos raios X dispersos interferem construtivamente. Para que as ondas interfiram construtivamente, as diferenças na trajectória de viagem devem ser iguais a múltiplos inteiros do comprimento de onda. Quando esta interferência construtiva ocorre, um feixe difratado de raios X deixará o cristal num ângulo igual ao do feixe incidente.
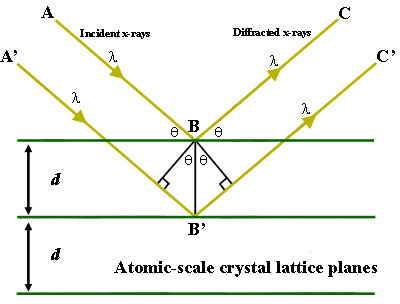
Figura 1. Reflexão da Lei de Bragg. Os raios X difratados exibem interferência construtiva quando a distância entre os caminhos ABC e A’B’C’ difere por um número inteiro de comprimentos de onda (λ).
Para ilustrar esta característica, considere um cristal com distâncias planas de malha de cristal d (direita). Quando a diferença do comprimento da trajectória de viagem entre as trajectórias de raios ABC e A’B’C’ é um múltiplo inteiro do comprimento de onda, ocorrerá interferência construtiva para uma combinação desse comprimento de onda específico, espaçamento planar da malha cristalina e ângulo de incidência (Θ). Cada plano racional de átomos num cristal sofrerá uma refracção num único e único ângulo (para raios X de um comprimento de onda fixo).
A relação geral entre o comprimento de onda dos raios X incidentes, ângulo de incidência e espaçamento entre os planos da malha de cristal de átomos é conhecida como Lei de Bragg, expressa como:
n λ = 2d sinΘ
onde n (um inteiro) é a “ordem” de reflexão, λ é o comprimento de onda dos raios X incidentes, d é o espaçamento interplanar do cristal e Θ é o ângulo de incidência.
Aplicações da Lei de Bragg.
- Na difracção de raios X (XRD), o espaçamento interplanar (d-espaçamento) de um cristal é utilizado para fins de identificação e caracterização. Neste caso, o comprimento de onda do raio X incidente é conhecido e é feita a medição do ângulo incidente (Θ) em que ocorre a interferência construtiva. A resolução da Equação de Bragg dá o espaçamento d entre os planos da malha de cristal dos átomos que produzem a interferência construtiva. Espera-se que um dado cristal desconhecido tenha muitos planos racionais de átomos na sua estrutura; portanto, a recolha de “reflexos” de todos os planos pode ser utilizada para identificar de forma única um cristal desconhecido. Em geral, os cristais com alta simetria (por exemplo, sistema isométrico) tendem a ter relativamente poucos planos atómicos, enquanto os cristais com baixa simetria (nos sistemas triclínico ou monoclínico) tendem a ter um grande número de possíveis planos atómicos nas suas estruturas.
- No caso da espectrometria dispersiva de comprimento de onda (WDS) ou espectroscopia de fluorescência de raios X (XRF), os cristais de espaçamento d conhecidos são utilizados como cristais de análise no espectrómetro. Como a posição da amostra e do detector é fixa nestas aplicações, a posição angular do cristal reflector é alterada de acordo com a Lei de Bragg para que um determinado comprimento de onda de interesse possa ser dirigido a um detector para análise quantitativa. Cada elemento da Tabela Periódica tem uma discreta diferença de energia entre as “conchas” orbitais (por exemplo, K, L, M), de tal forma que cada elemento produzirá raios X de um comprimento de onda fixo. Portanto, utilizando um cristal espectrómetro (com espaçamento d fixo do cristal) e posicionando o cristal num ângulo único e fixo (Θ), é possível detectar e quantificar elementos de interesse com base nos comprimentos de onda característicos dos raios X produzidos por cada elemento.
Literatura
Eby, G.N., 2004, Principles of Environmental Geochemistry. Brooks/Cole-Thomson Learning, p. 212-214.