Il modello dello spazio di stato del sistema lineare tempo-invariante (LTI) può essere rappresentato come,
${X}=AX+BU$
$Y$=CX+DU$
La prima e la seconda equazione sono note rispettivamente come equazione di stato e equazione di uscita.
Dove,
-
X e $documento{X}$ sono rispettivamente il vettore di stato e il vettore di stato differenziale.
-
U e Y sono rispettivamente il vettore di ingresso e il vettore di uscita.
-
A è la matrice del sistema.
-
B e C sono le matrici di ingresso e di uscita.
-
D è la matrice feed-forward.
Concetti di base del modello dello spazio di stato
La seguente terminologia di base coinvolta in questo capitolo.
Stato
È un gruppo di variabili, che riassume la storia del sistema al fine di prevedere i valori futuri (uscite).
Variabile di stato
Il numero delle variabili di stato richieste è uguale al numero degli elementi di memorizzazione presenti nel sistema.
Esempi – corrente che scorre attraverso l’induttore, tensione attraverso il condensatore
Vettore di stato
È un vettore, che contiene le variabili di stato come elementi.
Nei capitoli precedenti, abbiamo discusso due modelli matematici dei sistemi di controllo. Questi sono il modello di equazione differenziale e il modello di funzione di trasferimento. Il modello dello spazio di stato può essere ottenuto da uno qualsiasi di questi due modelli matematici. Ora discutiamo questi due metodi uno per uno.
Modello dello spazio di stato dall’equazione differenziale
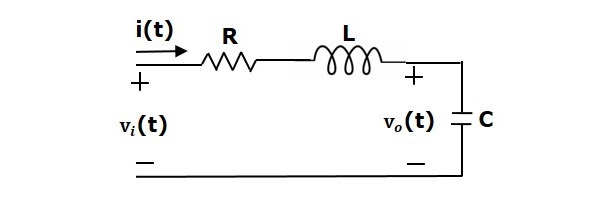
In questo circuito ci sono due elementi di memoria (induttore e condensatore). Quindi, il numero delle variabili di stato è uguale a due e queste variabili di stato sono la corrente che scorre attraverso l’induttore, $i(t)$ e la tensione attraverso il condensatore, $v_c(t)$.
Dal circuito, la tensione di uscita, $v_0(t)$ è uguale alla tensione attraverso il condensatore, $v_c(t)$.
$v_0(t)=v_c(t)$
Applica la KVL attorno al circuito.
$v_i(t)=Ri(t)+L\frac {testo{d}i(t)}+v_c(t)$
$$frac_a destra \frac{d}i(t){{testo{d}t}=-\frac{Ri(t)}{L}-{frac{v_c(t)}{L}+{frac{v_i(t)}{L}$
La tensione attraverso il condensatore è –
$v_c(t)={frac{1}{C} \int i(t) dt$
Differenzia l’equazione precedente rispetto al tempo.
$$frac{{d}v_c(t)}{frac{d}t}=frac{i(t)}{C}$
Vettore di stato, $X== inizio{bmatrice}i(t) \v_c(t) \fine{bmatrice}$
Vettore di stato differenziale, $dot{X}={begin{bmatrix}{frac{{bmatrix}i(t)}{brac{text{d}t} \\\frac{\text{d}v_c(t)}{\text{d}t}
Possiamo organizzare le equazioni differenziali e l’equazione di uscita nella forma standard del modello dello spazio di stato come,
$Y=0 & 1 \end{bmatrix}i(t) \v_c(t) \end{bmatrix}$
dove,
Modello dello spazio di stato dalla funzione di trasferimento
Considera i due tipi di funzioni di trasferimento in base al tipo di termini presenti nel numeratore.
- Funzione di trasferimento con termine costante nel numeratore.
- Funzione di trasferimento con funzione polinomiale di ‘s’ nel numeratore.
Funzione di trasferimento con termine costante nel numeratore
Considera la seguente funzione di trasferimento di un sistema
$$frac{Y(s)}{U(s)}=\frac{b_0}{s^n+a_{n-1}s^{n-1}+…+a_1s+a_0}$
Riorganizzare l’equazione precedente come
$(s^n+a_{n-1}s^{n-1}+…+a_0)Y(s)=b_0 U(s)$
Applicare la trasformata di Laplace inversa su entrambi i lati.
$\frac{\text{d}^ny(t)}{\text{d}t^n}+a_{n-1}\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}+…+a_1\frac{{text{d}y(t)}{text{d}t}+a_0y(t)=b_0 u(t)$
Lascia
$y(t)=x_1$
$\frac{\text{d}y(t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2y(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^ny(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then,
$\dot{x}_n+a_{n-1}x_n+…+a_1x_2+a_0x_1=b_0 u$
Dalla precedente equazione, possiamo scrivere la seguente equazione di stato.
$$dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+b_0 u$
L’equazione di uscita è –
$y(t)=y=x_1$
Il modello dello spazio di stato è –
$dot{X}===begin{bmatrix}{dot{x}_1 \\documento{x}_2 \documenti \documento{x}_{n-1} \\punto{x}_n \fine{bmatrice}$
$Y==punto iniziale{bmatrice}1 && \dotso && 0 \fine{bmatrice}x_1 \x_2 \vdots \x_{n-1} \x_n \end{bmatrix}$
Qui, $D=sinistra.$
Esempio
Trova il modello dello spazio di stato per il sistema con funzione di trasferimento.
$$frac{Y(s)}{U(s)}=\frac{1}{s^2+s+1}$
Riorganizza l’equazione di cui sopra come,
$(s^2+s+1)Y(s)=U(s)$
Applica la trasformata di Laplace inversa su entrambi i lati.
$$frac{{testo{d}^2y(t)}{testo{d}t^2}+$frac{testo{d}y(t)}{testo{d}t}+y(t)=u(t)$
Lascia
$y(t)=x_1$
$frac{{text{d}y(t)}{{text{d}t}=x_2={x}_1$
e $u(t)=u$
Allora, l’equazione di stato è
$$d{x}_2=-x_1-x_2+u$
L’equazione di uscita è
$y(t)=y=x_1$
Il modello dello spazio di stato è
$Y==begin{bmatrix}1 & 0 \end{bmatrix}\begin{bmatrix}x_1 \x_2
Funzione di trasferimento con funzione polinomiale di ‘s’ al numeratore
Consideriamo la seguente funzione di trasferimento di un sistema
$$frac{Y(s)}{U(s)}=\frac{b_n s^n+b_{n-1}s^{n-1}+…+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$
$$$Rightarrow \frac{Y(s)}{U(s)}=\left( \frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0} \destra )(b_n s^n+b_{n-1}s^{n-1}+…+b_1s+b_0)$
L’equazione di cui sopra è sotto forma di prodotto delle funzioni di trasferimento di due blocchi, che sono in cascata.
$$frac{Y(s)}{U(s)}===sinistra(\frac{V(s)}{U(s)} \right ) \sinistra(\frac{Y(s)}{V(s)} \$
Qui,
$$frac{V(s)}{U(s)}=\frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$
Riordina, l’equazione di cui sopra come
$(s^n+a_{n-1}s^{n-1}+…+a_0)V(s)=U(s)$
Applica la trasformata di Laplace inversa su entrambi i lati.
$$frac{frac{d}^nv(t)}{testo{d}t^n}+a_{n-1}{frac{d}^{n-1}v(t)}{testo{d}t^{n-1}}+…+a_1 \frac{{{text{d}v(t)}{{text{d}t}+a_0v(t)=u(t)$
Lascia
$v(t)=x_1$
$\frac{\text{d}v((t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2v(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^nv(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then, l’equazione di stato è
$$Dotato{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+u$
Consider,
$\frac{Y(s)}{V(s)}=b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0$
Riorganizza l’equazione di cui sopra come
$Y(s)=(b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0)V(s)$
Applica la trasformata di Laplace inversa su entrambi i lati.
$y(t)=b_n\frac{\text{d}^nv(t)}{\text{d}t^n}+b_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+…+b_1\frac{testo{d}v(t)}{testo{d}t}+b_0v(t)$
Sostituendo le variabili di stato e $y(t)=y$ nell’equazione precedente, si ottiene l’equazione di uscita come,
$y=b_n{dot{x}_n+b_{n-1}x_n+…+b_1x_2+b_0x_1$
Sostituire, il valore di $\dot{x}_n$ nell’equazione precedente.
$y=b_n(-a_0x_1-a_1x_2-…-a_{n-1}x_n+u)+b_{n-1}x_n+…+b_1x_2+b_0x_1$
$y=(b_0-b_na_0)x_1+(b_1-b_na_1)x_2+…+(b_{n-1}-b_na_{n-1})x_n+b_n u$
Il modello dello spazio di stato è
$\dot{X}==begin{bmatrix}\dot{x}_1 \documento{x}_2 \documenti \documento{x}_{n-1} \\doto{x}_n \fine{bmatrice}$
$Y=$ $begin{bmatrix}x_1 \x_2 \doto \x_{n-1} \x_n \fine{bmatrice}$
Se $b_n = 0$, allora,
$Y=$Y==begin{bmatrix}x_1 \x_2 \\vdots \x_{n-1} \x_n \end{bmatrix}$