Heading

Costruire scale per il vostro ponte, patio o giardino è un compito incredibilmente difficile.

Per fare questo, ci sono molti parametri e misure che devi inserire nei tuoi calcoli.

Ti mostriamo come questo può essere fatto facilmente 😉

Il nostro calcolatore di scale online può aiutarti a rendere questo compito un gioco da ragazzi.

Semplicemente inserisci i valori per la corsa totale e l’altezza, insieme ad alcune misure per i singoli gradini per calcolare la disposizione della tua scala!

Come calcolare le scale

Per usare il nostro calcolatore di scale, devi inserire le seguenti misure come minimo:

• Corsa totale – La lunghezza orizzontale totale della scala
• Altezza totale – L’altezza verticale tra il fondo del primo gradino e la cima dell’ultimo gradino nella scala
• Larghezza della scala – La misura diagonale totale tra il bordo del gradino e la linea di fondo
• Numero di gradini richiesti

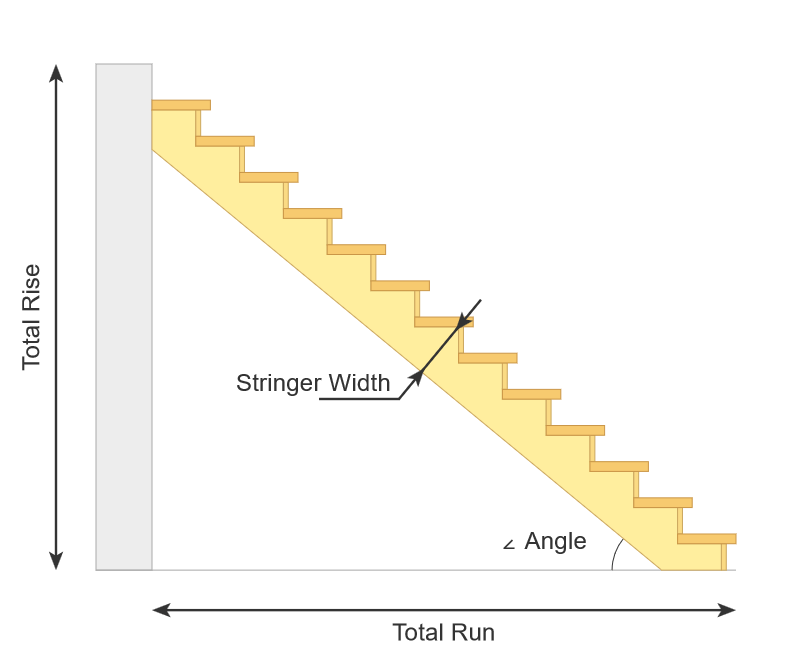
Utilizzando questi valori, la nostra calcolatrice calcola il dislivello verticale di ogni singolo gradino con la frazione:

$Rise = {Totale,Rise \sopra numero,di,gradini}$

Inoltre, il nostro calcolatore vi permette di scegliere tra un montaggio standard e uno a filo.

Decidere di usare un montaggio piuttosto che l’altro dipenderà dalla vostra situazione individuale e dal vostro progetto di fai da te.

Per aiutarvi a seguire l’articolo e la spiegazione queste formule sono piuttosto astratte e complicate.

Per aiutarvi a seguire l’articolo, faremo un esempio lavorato.

Questo serve a rendere i calcoli, le formule e le spiegazioni più facili da seguire.

Calcoli di esempio

• Per entrambi i nostri esempi qui sotto, immaginiamo di voler avere 17 gradini che corrono fino a un pianerottolo con un’altezza verticale totale di 120 pollici e una corsa orizzontale totale di 180 pollici
• Diciamo che abbiamo uno spessore del battistrada di 2 pollici
• Sovrapposizione del battistrada di 2 pollici
• Spessore del rialzo di 1 pollice
• E una larghezza del trave di 12 pollici

Vi porteremo attraverso i calcoli di esempio per un primo montaggio standard, e poi un set di scale con montaggio a filo.

Così facendo, calcoleremo le dimensioni dei gradini e della scala.

Inoltre, vi mostreremo come il calcolatore per scale calcola l’aumento, la corsa, l’angolo e la lunghezza della scala, permettendovi di pianificare efficacemente il layout della vostra scala.

Oppure, seguite questi calcoli o semplicemente usate il calcolatore per far partire il vostro progetto fai da te in un baleno!

Suona bene? 😀

Calcoli di montaggio standard

Prima di tutto, calcoliamo l’innalzamento verticale di ogni gradino:

$Rise = {Totale,Innalzamento \su numero\,di\,gradini} = {120\,in \su 17} = 7.06\,in$

Ora, usando una scala a montaggio standard, l’innalzamento verticale dei gradini sarà un gradino in meno che con un montaggio a filo, perché l’ultimo gradino è occupato dal rivestimento. Così, calcoliamo:

$Rise,of,steps = Total\Rise – Rise = 120\,in – 7.06\,in = 112.94\,in$

Ora, se includiamo lo spessore della pedata (lo spessore della pedata su ogni passo), dobbiamo sottrarre anche questo. La calcolatrice per le scale a ponte così calcola:

$Run,of,steps = Total\Run – (Tread,Overlap + Riser,Thickness) = 180\,in – (2\,in + 1\,in) = 177\,in$

Quindi, la nostra calcolatrice per le scale a ponte può calcolare la distanza orizzontale totale tra il bordo di ogni gradino (senza dimenticare che l’ultimo gradino è il decking!):

$Run = {Run,of\,steps \over Number\,of\,steps} = {177\,in \over 16} = 11.06\,in$

Ora, se consideriamo un singolo gradino della scala, la distanza orizzontale totale sarà data da:

$Totale,Distanza Orizzontale = Corsa + Battistrada,Sovrapposizione + Riser,Spessore = 11.06\,in + 2\,in + 1\,in = 14.06\,in$

E l’angolo (o passo!) tra l’orizzontale e la scala è calcolato da:

$$tan\,\alpha_1 = {Rise,of\,steps \over Run\,of\,steps} → \alpha_1 = tan^{-1} {Rise,of\,steps \over Run\,of\,steps} = tan^{-1} {112.94\,in \sopra 177\,in} = 32.54^o$

Ora, per trovare la lunghezza della scala richiede un po’ di matematica più complicata. 🧐

Continua a seguire l’esempio qui sotto per vederlo in dettaglio!

Se consideriamo la scala, l’angolo tra il gradino di sinistra e l’orizzontale (α2) è dato dalla sottrazione dell’angolo precedentemente calcolato da 90 gradi:

$\alpha_2 = 90^o – \alpha_1 = 90^o – 32.54^o = 57.46^o$

Similmente,

$alpha_3 = 90^o + \alpha_2 = 90^o + 57.46^o = 147.46^o$

E

$alpha_4 = \alpha_1 = 32.54^o$

$alpha_5 = 90^o + \alpha_1 = 90^o + 32.54^o = 122.54^o$

Inoltre, la calcolatrice è in grado di calcolare le dimensioni orizzontali e verticali del longherone.

Per facilità di comprensione, di nuovo, vedi l’immagine di riferimento. La calcolatrice calcola tutte queste distanze utilizzando il metodo indicato di seguito:

$A_1 = Rise × sin\,\alpha_2 = 7.06\,in × sin\,57.46^o = 5.95\,in$

$A_2 = Stringer\ larghezza – A_1 = 12\,in – 5.95\,in = 6.05\,in$

$C_2 = \sqrt{Run^2 – {A_1}^2} = \sqrt{(11.06\,in)^2 – (5.95\,in)^2} = 9.32\,in$

$C_3 = A_1 × tan\,\alfa_2 = 5.95\,in × tan\,57.46^o = 9.33\,in$

$B_1 = \sqrt{Risorsa^2 – {A_1}^2} = \sqrt{(7.06,in)^2- (5.95\,in)^2} = 3.8\,in$

$B_2 = A_2 × tan\,\alpha_1 = 6.05\,in × tan\,32.54^o = 3.86\,in$

$B_3 = (Rise -Tread\,Thickness) × cos\,\alpha_2 = (7.06\,in – 2\,in) × cos\,57.46^o = 2.72\,in$

$A_3 = (Rise – Tread,Thickness) × cos\,\alpha_1 = (7.06\,in – 2\,in) × cos\,32.54^o = 4.26\,in$

$A_4 = Stringer,Width – A_3 = 12\,in – 4.27\,in = 7.74\,in$

$C_4 = A_4 × tan\,\alfa_2 = 7.74\,in × tan\,57.46^o = 12.12\,in$

Infine, la calcolatrice combina i valori calcolati sopra per calcolare la lunghezza totale dei gradini:

$Stringer\Lunghezza = C_3 + B_3 + (numero di gradini – 1) × (B_1 + C_2) = 9.33\,in + 2.72\,in + (16-1) × (3.8\,in + 9.32\,in) = 208.88\,in$

Calcoli per il montaggio a filo

Calcolare la salita, la corsa, l’angolo e la lunghezza della trave per un montaggio a filo è molto simile al montaggio standard.

Ricordiamo semplicemente che l’ultimo passo ci porta sulla terrazza.

Come prima, calcoliamo l’innalzamento verticale:

$Rise = {Totale,innalzamento \su numero,di,passi} = {120,in \su 17} = 7.06\,in$

A differenza della misura del montaggio standard, dove abbiamo sottratto il gradino finale dal rialzo, con un montaggio a filo abbiamo che:

$Risalita,di,passi = Totale,Rialzo = 120\,in$

Tuttavia, sul gradino superiore, non avremo alcuna pedata (perché il gradino finale è il decking stesso!) Quindi, trasformiamo le formule di cui sopra per ottenere la distanza verticale di salita:

$$Rise,of,steps = Total\Rise – Tread\,Thickness = 120\,in – 2\,in = 118\,in$

Come prima, includendo la pedata quando si considera la corsa dei passi si ottiene:

$Run,of,steps = Total,Run – (Tread,Overlap + Riser,Thickness) = 180\,in – (2\,in + 1\,in) = 177\,in$

Quindi, la nostra calcolatrice calcola la distanza orizzontale totale tra il bordo di ogni passo.

La differenza qui è che abbiamo 17 passi, dato che l’ultimo passo è incluso nel montaggio a filo!

$Run = {Run,di passi \su Numero,di passi} = {177\,in \su 17} = 10.41\,in$

Considerando un singolo passo, la distanza orizzontale totale sarà data da:

$$Totale,Distanza Orizzontale,= Corsa + Battistrada,Sovrapposizione + Riser,Spessore = 10.41\,in + 2\,in + 1\,in = 13.41\,in$

E l’angolo tra l’orizzontale e le scale è ancora una volta dato da:

$tan\,\alfa_1 = {Rise,of\,steps \over Run\,of\,steps} → \alfa_1 = tan^{-1} {Rise,of\,steps \over Run\,of\,steps} = tan^{-1} {120\,in \over 177\,in} = 34.14^o$

Calcolare la lunghezza del longherone è lo stesso metodo del montaggio standard.

La calcolatrice calcola prima gli angoli:

$alpha_2 = 90^o – \alpha_1 = 90^o – 34.14^o = 55.86^o$

$alpha_3 = 90^o + \alpha_2 = 90^o + 55.86^o = 145,86^o$

$alpha_4 = \alpha_1 = 34,14^o$

$alpha_5 = 90^o + \alpha_1 = 90^o + 34,14^o = 124.14^o$

E la calcolatrice calcola la distanza per le lunghezze come prima:

$A_1 = Rise × sin\\,\alpha_2 = 7.06\,in × sin\,55.86^o = 5.84\,in$

$A_2 = Stringer\ larghezza – A_1 = 12\,in – 5.84\,in = 6.16\,in$

$C_2 = \sqrt{Run^2 – {A_1}^2} = \sqrt{(10.41\,in)^2 – (5.84\,in)^2} = 8.62\,in$

$C_3 = A_1 × tan\,\alpha_2 = 5.84\,in × tan\,55.86^o = 8.62\,in$

$B_1 = \sqrt{Rise^2 – {A_1}^2} = \sqrt{(7.06\,in)^2- (5.84\,in)^2} = 3.96\,in$

$B_2 = A_2 × tan\,\alpha_1 = 6.16\,in × tan\ 34,14^o = 4,17\,in$

$B_3 = (Rise -Tread,Thickness) × cos\,\alpha_2 = (7,06\,in – 2\,in) × cos\,55.86^o = 2.84\,in$

$A_3 = (Rise – Tread\,Thickness) × cos\,\alpha_1 = (7.06\,in – 2\,in) × cos\,34.14^o = 4.19\,in$

$A_4 = Stringer,Width – A_3 = 12\,in – 4.19\,in = 7.81\,in$

$C_4 = A_4 × tan,\alpha_2 = 7.81\,in × tan\55,86^o = 11,52\,in$

Infine, la calcolatrice calcola la lunghezza totale della stringa come prima:

$Stringer\Lunghezza = C_3 + B_3 + (Numero di passi – 1) × (B_1 + C_2) = 8.62\,in + 2.84\,in + (17-1) × (3.96\,in + 8.62\,in) = 212.72\,in$

Fa attenzione! ⚠️

Assicurati di non arrotondare la risposta prima del calcolo finale. Questi piccoli errori di arrotondamento possono avere una grande differenza sulla risposta finale!

Capiamo che questo è piuttosto difficile da seguire! State tranquilli, se non capite questo, non preoccupatevi.

Il calcolatore fa tutto questo per voi, spostando l’enfasi e la preoccupazione da voi alla tecnologia. 😉

Domande frequenti

• Quali linee guida o regolamenti devo considerare quando pianifico di costruire una serie di scale?

Si consiglia di essere a conoscenza di tutti i regolamenti edilizi del proprio paese.

Il nostro calcolatore è programmato per dare misure accurate all’interno delle linee guida del Council of American Building Officials e International Code Council.

• Quali proprietà devono soddisfare i regolamenti edilizi del mio paese per scale e scale?

Per una risposta esatta dovreste controllare i regolamenti edilizi del vostro paese d’origine.

Tuttavia, una buona guida è che qualsiasi attività o chiesa, organizzazione, ufficio o proprietà commerciale dovrebbe soddisfare gli standard per le scale del vostro paese d’origine.

Fate attenzione – vi aprite a potenziali multe sostanziali se non rispettate gli standard per le scale.

Utilizzate il nostro calcolatore, fate qualche ricerca e seguite gli esempi di cui sopra per assicurarvi di rispettarli prima di iniziare!

• Cosa succede se le misure delle mie scale sono in altre unità metriche o imperiali?

La risposta è molto semplice! Il nostro calcolatore può lavorare in molte unità diverse allo stesso tempo.

Il calcolatore fa le conversioni per te usando i seguenti rapporti:

$1\,foot = 12\,inches = 0.33\,iarde = 30.48\,centimetri = 0.3048\,metri$

È così facile! 🙂

• Le scale di casa mia devono soddisfare gli standard locali?

No! Come regola generale, gli standard del regolamento edilizio sulle scale sono applicabili per le proprietà commerciali che utilizzano scale permanenti, non per le tipiche scale domestiche, temporanee o portatili per uso personale.

• C’è qualche guida o consiglio su quanto dovrebbero essere lunghe le mie scale?

Una buona linea guida è data dal Council of American Building Officials e dall’International Code Council.

Questi regolamenti raccomandano che la salita delle scale non sia più di 7,75 pollici (17,78 cm) e che la corsa delle scale non sia meno di 10 pollici (25. 4 cm).4 cm).

Non dimenticate però che questo è per una proprietà commerciale.

Questo potrebbe non essere pratico o necessario per la vostra casa, dove le vostre scale non devono soddisfare gli stessi standard commerciali, ma dovrebbero essere usati come una guida.

• Dove posso trovare maggiori informazioni sugli standard delle scale per le proprietà commerciali?

Ci sono molte informazioni che possono essere trovate online.

Consigliamo questo sito web come ottimo punto di partenza: https://codes.iccsafe.org/content/IBC2018P4/chapter-10-means-of-egress#IBC2018P4_Ch10_Sec1011. La sezione 1011 ha molte informazioni dal codice edilizio internazionale del 2018.