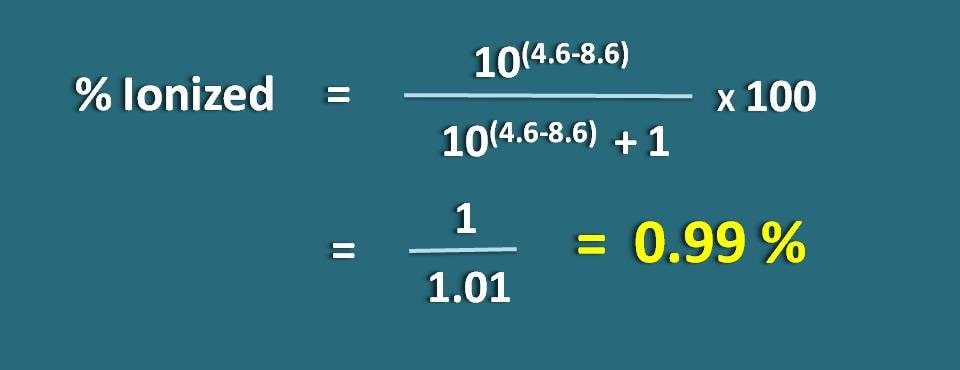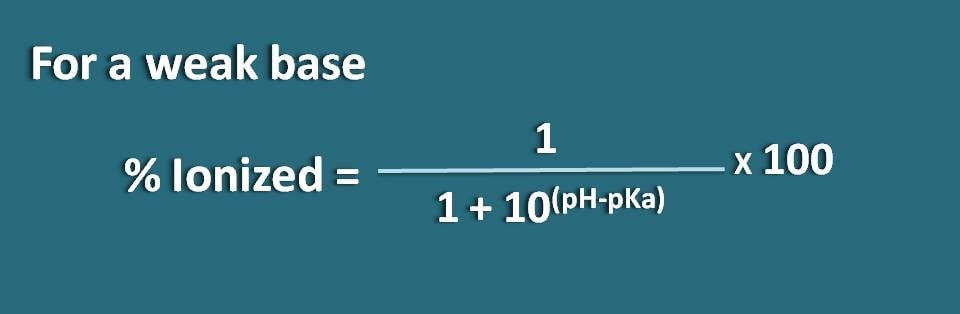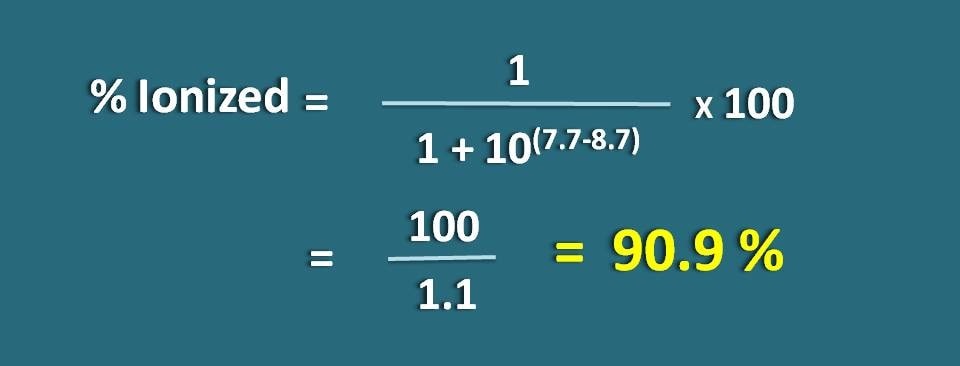Manchmal müssen wir den Ionisierungszustand einer organischen Verbindung kennen, um einige der physikalisch-chemischen Eigenschaften der Verbindung zu beurteilen. Wenn die Verbindung zum Beispiel bei einem bestimmten pH-Wert stärker ionisiert ist, hat sie eine höhere Wasserlöslichkeit. Wenn wir uns andererseits auf die Permeabilität der Verbindung durch eine physiologische Membran konzentrieren, dann ist die ionisierte Form der Verbindung wichtiger, da sie lipophiler ist und die lipophile Membran durchqueren kann.
Die Berechnung der prozentualen Ionisierung ist also eine wesentliche Aufgabe, auf die wir oft stoßen, wenn wir uns mit der Pharmakokinetik von Medikamenten beschäftigen. Hier sehen wir, wie wir sie zusammen mit einigen Beispielen berechnen können.
Henderson-Hasselbalch-Gleichung
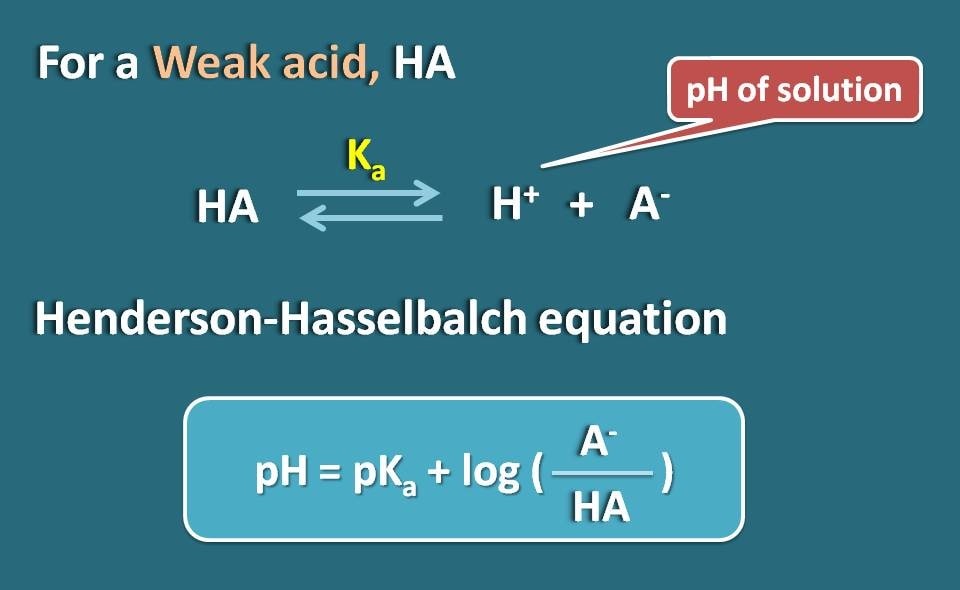
Lassen Sie uns einen schwachen Elektrolyten wie HA nehmen, der wie eine schwache Säure wirkt. Wenn es in Wasser gelöst ist, wird es nicht vollständig ionisiert, sondern erreicht ein Gleichgewicht, so dass es sowohl in ionisierter als auch in unionisierter Form existieren kann.
Indem wir die Henderson-Hasselbach-Gleichung für die schwache Säure anwenden, können wir den pH-Wert der Lösung mit dem pKa-Wert des Wirkstoffs und seiner Ionisierung in Beziehung setzen.
So, pH=pKa + log(A-/HA)
Wobei A- die ionisierte Form der schwachen Säure ist, während HA die unionisierte Form ist.
Nun lassen Sie uns diese Gleichung so umstellen, dass wir das Verhältnis von ionisierter zu unionisierter Form der schwachen Säure erhalten.
log(A-/HA)=pH – pKa
Nimmt man den Antilogarithmus,
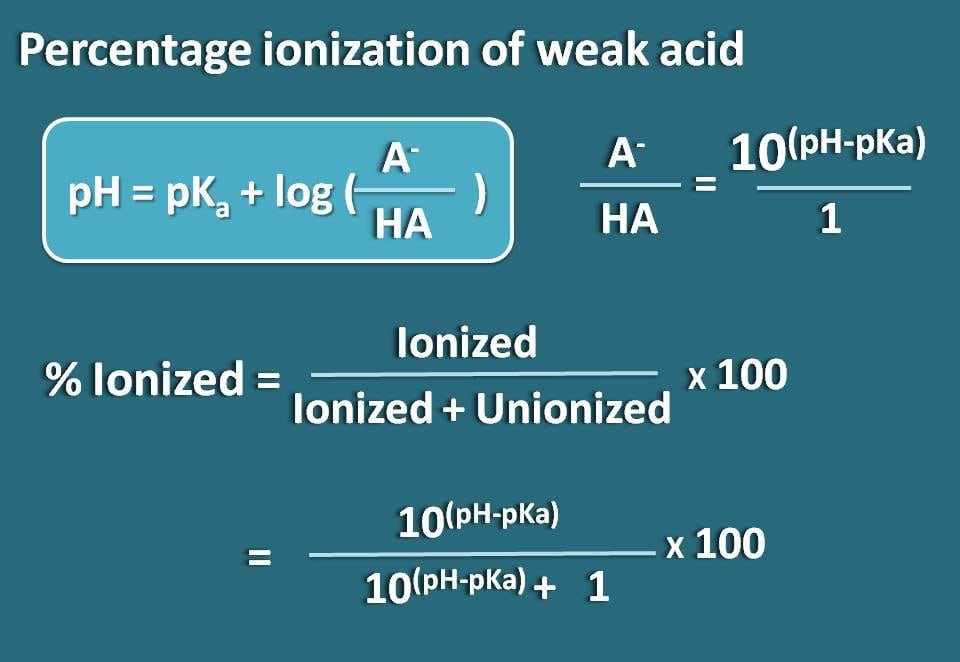
A-/HA=10(pH – pKa)
Nun kennen wir das Verhältnis der ionisierten Form zur unionisierten Form. Daraus können wir die prozentuale Ionisierung berechnen.
% ionisiert= * 100
Einsetzen in diese Gleichung,
% ionisiert=* 100
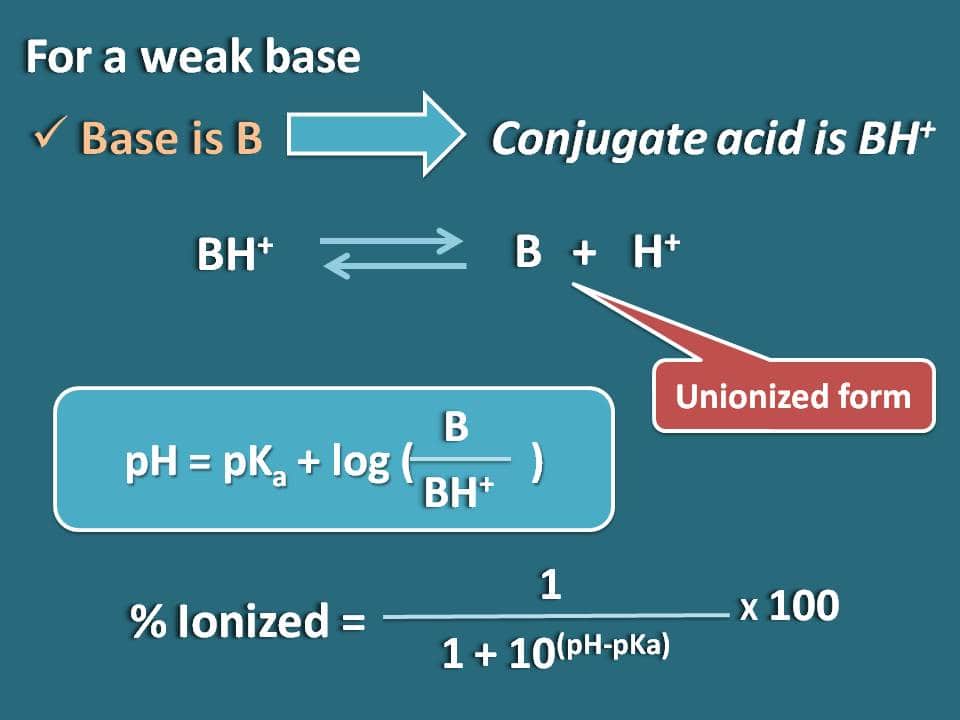
Ahnlich können wir die Formel für eine schwache Base wie B erhalten, deren konjugierte Säure BH+ ist. Nun können wir das chemische Gleichgewicht für die konjugierte Säure wie folgt schreiben.
Nun schreiben wir die Hendersen-Hasselbalch-Gleichung für die konjugierte Säure
pH=pKa + log (B/BH+)
Nun kann das Verhältnis von unionisierter zu ionisierter Form der Base wie folgt geschrieben werden
B/BH+=10(pH – pKa)
Hier ist der Anteil der unionisierten Form 10(pH – pKa), während die ionisierte Form 1 ist. Also ist die prozentuale Ionisierung
% ionisiert=* 100
Alternativ, können wir die obige Gleichung auch umstellen, indem wir den Term pH-pKa in pKa-pH umkehren, wodurch wir die Formel als
% ionisiert=* 100
Nun lassen Sie uns mit einigen praktischen Beispielen fortfahren und sehen, wie wir sie lösen können.
Arbeitsbeispiel 1
Berechnen Sie die prozentuale Ionisierung eines schwach sauren Medikaments bei einem pH-Wert von 4,6 und einem pKa-Wert von 8,6.
Lösung:
Zunächst listen wir die gegebenen Daten auf.
pH=4,6 und pKa=8,6
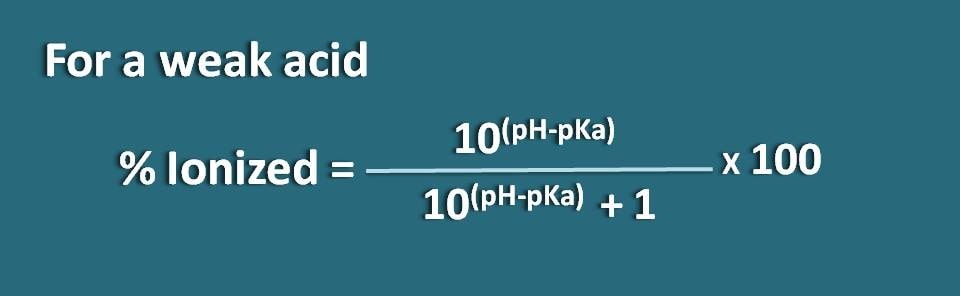
Da es sich um einen schwach sauren Arzneistoff handelt, wenden wir die folgende Formel an.
Einsetzen in die obige Gleichung,
% ionisiert=* 100
=1/1.01=0.99 %
Lassen Sie uns mit einem anderen Beispiel fortfahren.
Arbeitsbeispiel 2
Berechnen Sie den Anteil des Arzneimittels in der ionisierten Form bei pH 7.7 eines Gewebes für einen basischen Arzneistoff mit pKa 8,7.
Lösung:
Zunächst seien die gegebenen Daten aufgeführt.
pH=7.7 und pKa=8.7
Hier handelt es sich um eine schwache Base, also müssen wir die folgende Formel anwenden.
Einsetzen in die obige Gleichung,
% ionisiert=* 100
=100/1.1=90,9 %
Abschließend noch ein anderes Beispiel.
Arbeitsbeispiel 3
Berechnen Sie das Verhältnis der protonierten zu den unprotonierten Formen von Morphin bei pH 5. pKa von Morphin ist 7.
Lösung:
Auch hier ist das gegebene Datum pH=5 und pKa=7.
Morphin ist ein opioides Analgetikum, das tertiäres Amin im Ring hat und daher als schwache Base wirkt. Hier wurde aber nach dem Verhältnis von protonierter zu unprotonierter Form des Medikaments gefragt. Die protonierte Form ist nichts anderes als die ionisierte Form, während die unprotonierte Form die unionisierte Form ist. Für eine schwache Base ist das Verhältnis 10(pH – pKa) : 1.
Lassen Sie uns die Werte ersetzen.
Protoniert/ unprotoniert=10(5 – 7)/1