Las órdenes del rey son un gran rompecabezas
(Dificultad: Fácil)
El rey Nupe del reino de Catán adora tanto a sus dos hijas que decide que el reino estaría mejor con más niñas que niños, y hace el siguiente decreto: Todas las parejas que tengan hijos deben seguir teniendo hijos hasta que tengan una hija!
Pero para evitar la superpoblación, hace un decreto adicional: Todas las parejas con hijos dejarán de tenerlos una vez que tengan una hija. Sus súbditos comienzan inmediatamente a seguir sus órdenes.
Después de muchos años, ¿cuál es la proporción esperada de niñas y niños en Catan?
Pista
La probabilidad de que cada bebé que nazca sea una niña es, por supuesto, del 50%.
Solución
¿Listo para la solución? Pincha aquí para ver si aciertas.
¿Cuántos huevos pone esta gallina?
(Dificultad: Fácil)
Este problema es en honor a mi padre, Harold Feiveson. A él se debe que me gusten los rompecabezas matemáticos, y este es uno de los primeros problemas (de muchos) que me dio cuando crecía.
Una gallina y media pone un huevo y medio en un día y medio. Cuántos huevos pone una gallina en un día?
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.
El problema matemático de la cadena de oro es engañosamente sencillo
(Dificultad: Moderada)
Estás rebuscando en el desván de tu bisabuela cuando encuentras cinco cadenas cortas formadas cada una por cuatro eslabones de oro. Se te ocurre que si las combinas todas en un gran lazo de 20 eslabones, tendrías un collar increíble. Así que lo llevas a una joyera, que te dice que el coste de hacer el collar será de 10 dólares por cada eslabón de oro que tenga que romper y luego volver a cerrar.
¿Cuánto te costará?
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.
Intenta resolver este puzzle de pickleball
(Dificultad: 🚨Difícil🚨)
Kenny, Abby y Ned se han reunido para disputar un torneo de pickleball de ida y vuelta, en el que, como es habitual, el ganador se queda después de cada partido para jugar contra la persona que se quedó fuera de ese partido. Al final de la tarde de pickleball, Abby está agotada, ya que ha jugado los últimos siete partidos seguidos. Kenny, que está menos agotado, hace un recuento de las partidas jugadas:
Kenny ha jugado ocho partidas
Abby ha jugado 12 partidas
Ned ha jugado 14 partidas
¿Quién ha ganado la cuarta partida contra quién?
Pista
¿Cuántas partidas en total se han jugado?
Solución
¿Listo para la solución? Pincha aquí para ver si aciertas.
Nuestro acertijo de los interruptores es pura maldad. Lo siento.
(Dificultad: 🚨Difícil🚨)
La caja de interruptores de tu nueva casa está en un rincón incómodo de tu sótano. Para su disgusto, descubre que ninguno de los 100 disyuntores está etiquetado, y se enfrenta a la desalentadora perspectiva de hacer coincidir cada disyuntor con su respectiva luz. (Supongamos que cada disyuntor se asigna a una sola luz.)
Para empezar, enciende las 100 luces de la casa y luego se dirige al sótano para comenzar el oneroso proceso de asignación. En cada viaje al sótano, puedes encender o apagar cualquier número de interruptores. A continuación, puede recorrer los pasillos de su casa para descubrir qué luces están encendidas y cuáles están apagadas.
¿Cuál es el número mínimo de viajes que tiene que hacer al sótano para asignar cada disyuntor a cada luz?
Pista
La solución no pasa por encender o apagar los interruptores de la luz de tu casa ni por sentir lo calientes que están las bombillas. Quizá quieras intentar resolver primero el caso de 10 interruptores sin etiquetar.
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.
Dos trenes. Dos abuelas. ¿Puedes resolver esta complicada adivinanza matemática?
(Dificultad: Moderada)
Las dos abuelas de Jesse quieren verlo todos los fines de semana, pero viven en lados opuestos de la ciudad. Como compromiso, les dice que todos los domingos se dirigirá a la estación de metro más cercana a su apartamento a una hora aleatoria del día y se subirá al siguiente tren que llegue.
Si resulta ser el tren que viaja hacia el norte, visitará a su abuela Erica en el centro, y si resulta ser el tren que viaja hacia el sur, visitará a su abuela Cara en el centro. Sus dos abuelas están de acuerdo con este plan, ya que saben que tanto el tren que va hacia el norte como el que va hacia el sur pasan cada 20 minutos.
Pero después de unos meses de hacer esto, la abuela Cara se queja de que sólo lo ve uno de cada cinco domingos. Jesse promete que, efectivamente, se dirige a la estación a una hora aleatoria cada día. Cómo puede ser esto?
Pista
Los trenes siempre llegan a sus horas programadas.
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.
Aquí tienes un Problema Matemático Realmente F@*#ing Difícil sobre Hormigas
(Dificultad: 🚨HARD🚨)
Max y Rose son hermanos hormiga. Les encanta hacer carreras entre ellos, pero siempre empatan, ya que en realidad se arrastran exactamente a la misma velocidad. Así que deciden crear una carrera en la que uno de ellos (con suerte) ganará.
Para esta carrera, cada uno de ellos empezará en la esquina inferior de un cuboide, y luego se arrastrará tan rápido como pueda para alcanzar una miga en la esquina opuesta. Las medidas de sus cuboides son las que aparecen en la imagen:
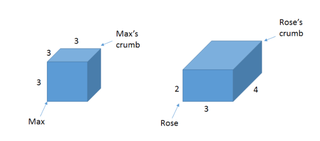
Si ambos toman el camino más corto posible para llegar a su miga, ¿quién llegará primero a su miga? (No olvides que son hormigas, así que, por supuesto, pueden trepar por cualquier parte de los bordes o de la superficie del cubo.)
Pista
Recuerda: Piensa fuera de la caja.
Solución
¿Listo para la solución? Pincha aquí para ver si aciertas.
Este acertijo de Peppermint Patty es prácticamente imposible
(Dificultad: 🚨HARD🚨)
Tienes que enfrentarte a tu amiga, Caryn, en un «concurso de caramelos», que funciona de la siguiente manera: Hay una pila de 100 caramelos y un caramelo de menta. Tú y Caryn iréis de un lado a otro cogiendo al menos uno y no más de cinco caramelos del montón en cada turno. La persona que saque el último caramelo se llevará también la hamburguesa de menta. Y a ti te encantan las hamburguesas de menta.
Supongamos que Caryn te deja decidir quién va primero. A quién deberías elegir para asegurarte de ganar la hamburguesa de menta?
Pista
Primero, resuelve por un montón de 10 caramelos.
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.
¿Puedes resolver el acertijo del Gran Sendero Ferroviario Americano?
(Dificultad: Moderada)
Este problema fue sugerido por el físico P. Jeffrey Ungar.
¡Por fin se ha completado el Gran Sendero Ferroviario Americano a través de todo el país! Adelante, dale una palmadita en la espalda: acabas de instalar la barandilla más larga de la historia del mundo, con 4.000 millas de principio a fin. Pero justo después de la ceremonia de inauguración, tu ayudante te recuerda que el metal que has utilizado para la barandilla se dilata ligeramente en verano, por lo que su longitud aumentará una pulgada en total.
«¡Ja!», dices, «¿Una pulgada en una barandilla de 4.000 millas? Eso no es nada!» Pero… ¿tienes razón?
Supongamos que cuando el pasamanos se expande, se dobla hacia arriba en su punto más débil, que está en el centro. Cuánto más alto tendrán que llegar los peatones del centro en verano para agarrarse a la barandilla? Es decir, en la figura de abajo, ¿cuál es h? (A efectos de esta pregunta, ignora la curvatura de la Tierra y asume que el camino es una línea recta.)
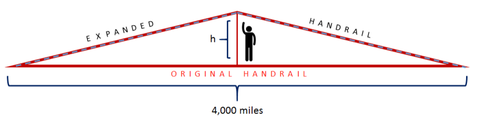
Pista
Pitágoras es una figura histórica fascinante.
Solución
¿Listo para la solución? Pincha aquí para ver si aciertas.
Este acertijo es como un problema de selectividad especialmente cruel. ¿Puedes encontrar la respuesta?
(Dificultad: Moderada)
Amanda vive con su hijo adolescente, Matt, en el campo, a un paseo en coche del colegio de Matt. Todas las tardes, Amanda sale de casa a la misma hora, conduce hasta el colegio a una velocidad constante, recoge a Matt exactamente cuando termina su club de ajedrez a las 5 de la tarde, e inmediatamente después vuelven juntos a casa a la misma velocidad constante. Pero un día, Matt no se encuentra bien, por lo que deja el entrenamiento de ajedrez antes de tiempo y comienza a dirigirse a casa en su patinete portátil.
Después de que Matt haya estado patinando durante una hora, Amanda se cruza con él en su coche (en su ruta habitual para recogerlo), y regresan juntos, llegando a casa 40 minutos antes de lo habitual. Cuánto tiempo de práctica de ajedrez se ha perdido Matt?
Pista
Considera el caso en el que Amanda se encuentra con Matt exactamente al salir de su casa.
Solución
¿Listo para la solución? Pincha aquí para ver si aciertas.
¿Puedes llevar a estas 3 estrellas de cine al otro lado del río?
(Dificultad: Moderada)
Tres estrellas de cine, Chloe, Lexa y Jon, están rodando una película en el Amazonas. Son muy famosos y muy exigentes, por lo que sus agentes están siempre con ellos. Un día, después de rodar una escena en lo más profundo de la selva, los tres actores y sus agentes deciden volver a la base a pie. De repente, llegan a un gran río.
En la orilla del río, encuentran un pequeño bote de remos, pero sólo es lo suficientemente grande para que quepan dos de ellos a la vez. ¿El problema? Ninguno de los agentes se siente cómodo dejando a su estrella de cine con otros agentes si ellos no están allí también. No confían en que los otros agentes no intenten robarles su estrella.
Por ejemplo, el agente de Chloe está bien si Chloe y Lexa están solas en el barco o en una de las orillas del río, pero definitivamente no está bien si el agente de Lexa también está con ellas. Entonces, ¿cómo pueden cruzar todas el río?
Pista
No hay una sola manera de resolver este problema.
Solución
¿Listo para la solución? Haz clic aquí para ver si aciertas.
Este acertijo ridículamente difícil es nuestro homenaje a un difunto genio de las matemáticas. ¿Puedes resolverlo?
(Dificultad: 🚨HARD🚨)
El 11 de abril, John Horton Conway, un brillante matemático que tenía una intensa y lúdica afición por los rompecabezas y los juegos, falleció por complicaciones del COVID-19. Conway es el inventor de uno de mis problemas legendarios favoritos (no apto para los débiles de corazón) y, famosamente, del Juego de la Vida. Creé este problema en su honor.
Carol estaba creando un árbol genealógico, pero tuvo problemas para localizar la fecha de nacimiento de su madre. La única pista que encontró fue una carta escrita por su abuelo a su abuela el día en que nació su madre. Por desgracia, algunos de los caracteres estaban borrados, representados aquí con un «___». (La longitud de la línea no refleja el número de caracteres emborronados.)
«Querida Virginia,
Poco sabía yo cuando me dirigía al trabajo este lunes por la mañana, que por la tarde tendríamos una preciosa niña. Y nada menos que en nuestro aniversario de boda. Me hace pensar en ese increíble día del fin de semana, el 27 de J___ de 19___, cuando compartimos por primera vez nuestro voto de crear una familia juntos, y, bueno, ¡aquí estamos! Feliz octavo aniversario, mi amor.
Amor, Edwin»
La pregunta: ¿Cuándo nació la madre de Carol?
Pista
Este problema está inspirado en la Regla del Juicio Final de Conway.
Solución
¿Listo para la solución? Haz clic aquí para ver si aciertas.
Para resolver este retorcido acertijo matemático, sólo necesitas un cinturón y una Tierra
(Dificultad: Moderada)
Imagina que tienes un cinturón muy largo. Bueno, extremadamente largo, en realidad… de hecho, es lo suficientemente largo como para poder envolver cómodamente la circunferencia de todo nuestro planeta. (Para simplificar, supongamos que la Tierra es perfectamente redonda, sin montañas, océanos u otras barreras en el camino del cinturón.)
Naturalmente, estás muy orgulloso de tu cinturón. Pero entonces aparece tu hermano, Peter, y para tu disgusto, presenta un cinturón que es un poco más largo que el tuyo. Se jacta de que su cinturón es más largo exactamente por su altura: 1,80 metros.
Si Peter también envolviera su cinturón alrededor de la circunferencia de la Tierra, ¿a qué distancia por encima de la superficie podría suspender el cinturón si tirara de él de forma tensa y uniforme?
Pista
La circunferencia de la Tierra es de unas 25.000 millas, o 130 millones de pies… pero no necesitas saberlo para resolver este problema.
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.
Este acertijo de los codos es diabólico. Buena suerte para resolverlo.
(Dificultad: 🚨HARD🚨)
En algún momento futuro, cuando se levanten las prohibiciones de refugiarse en el lugar, un matrimonio, Florian y Julia, se dirigen a un bar para celebrar su nueva libertad.
Encuentran allí a otras cuatro parejas que han tenido la misma idea.
Ansiosos por el contacto social, cada persona de las cinco parejas se codea con entusiasmo (el nuevo apretón de manos) con cada persona que aún no conoce.
En realidad, resulta que muchas de las personas se conocían de antes, así que cuando Julia les pregunta a todos cuántos codos se dieron, ¡obtiene sorprendentemente nueve respuestas diferentes!
La pregunta: ¿Cuántos codos dio Florian?
Pista
¿Qué nueve respuestas escuchó Julia?
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.
Necesitarás un trago después de intentar resolver este acertijo sobre el whisky
(Dificultad: Fácil)
Alan y Claire viven según el viejo dicho escocés: «¡Nunca tengas whisky sin agua, ni agua sin whisky!». Así que un día, cuando Alan tiene delante un vaso de whisky, y Claire tiene delante un vaso de agua del mismo tamaño, Alan coge una cucharada de su whisky y la pone en el agua de Claire.
Claire remueve su agua teñida de whisky, y luego vuelve a poner una cucharada de esta mezcla en el whisky de Alan para asegurarse de que tienen exactamente la misma cantidad para beber.
Entonces: ¿Hay más agua en el whisky de Alan, o más whisky en el agua de Claire? Y, ¿importa lo bien que revuelva Claire?
Pista
El tamaño de la cuchara no importa.
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.
El problema del garabato es mucho más difícil de lo que parece. Puedes resolverlo?
(Dificultad: Moderada)
El acertijo de esta semana es relativamente sencillo-pero siniestro igualmente.
La pregunta: ¿Puedes hacer 100 intercalando cualquier número de signos positivos y negativos dentro de la cadena de dígitos 9 8 7 6 5 4 3 2 1? ¡No se puede cambiar el orden de los dígitos! Entonces, ¿cuál es el menor número de más y menos necesarios para hacer 100?
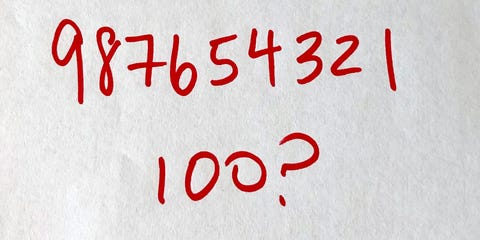
Por ejemplo, 98 – 7 – 6 + 54 – 32 muestra una forma de intercalar los más y los menos, pero como es igual a 107, no es una solución.
Yo llamo a esto un «problema de garabatos»: uno en el que es mejor trabajar durante las reuniones en las que podrías estar haciendo garabatos de otra manera.
Pista
Es posible que quieras empezar a buscar soluciones que usen un total de siete más y menos (aunque hay maneras de usar menos).
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.
Este acertijo matemático dejó perplejos a todos los científicos menos a uno. ¿Crees que puedes resolverlo?
(Dificultad: Difícil)
En honor a Freeman Dyson, el renombrado físico que falleció el mes pasado, he aquí una legendaria historia que demuestra su rápido ingenio y su increíble poder cerebral.
Un día, en una reunión de científicos de alto nivel, uno de ellos se preguntó en voz alta si existe un número entero que se pueda duplicar exactamente moviendo su último dígito hacia adelante. Por ejemplo, 265 lo satisfaría si 526 fuera su doble exacto -que no lo es-.
Después de aparentemente sólo cinco segundos, Dyson respondió: «Por supuesto que existe, pero el número más pequeño de este tipo tiene 18 dígitos».
Esto dejó a algunos de los científicos más inteligentes del mundo perplejos sobre cómo pudo haberlo descubierto tan rápidamente.
Entonces, dada la pista de Dyson, ¿cuál es el número más pequeño de este tipo?
Pista
Mi hijo de segundo grado ha aprendido recientemente a sumar un número de 3 cifras a sí mismo utilizando el clásico método vertical:

Los números de 18 cifras, por supuesto, se pueden sumar de la misma manera.
Solución
¿Listo para la solución? Pincha aquí para ver si aciertas.
Descubre qué hay en su frente
(Dificultad: Moderada)
A Cecilia le encanta poner a prueba la lógica de sus muy lógicos amigos Jaya, Julián y Levi, así que anuncia:
«Voy a escribir un número positivo en la frente de cada uno de vosotros. Ninguno de los números es igual, y dos de los números suman el tercero.»
Escribe los números en sus cabezas, luego se dirige a Jaya y le pregunta cuál es su número. Jaya ve que Julian tiene el 20 en la frente y Levi el 30 en la suya. Ella piensa un momento y luego dice: «No sé cuál es mi número». Julian interviene: «Yo tampoco sé mi número», y entonces Levi exclama: «¡Yo tampoco!». Cecilia dice alegremente: «¡Por fin os he dejado perplejos!».
«¡No tan rápido!» Dice Jaya. «¡Ahora ya sé mi número!».
¿Cuál es el número de Jaya?
Pista
Jaya podría ser uno de los dos números, pero sólo uno de ellos llevaría a que tanto Julián como Levi no supieran sus números. Por qué?
Solución
¿Listo para la solución? Pincha aquí para ver si aciertas.
¿Puedes conseguir que Keanu Reeves sea elegido presidente?
(Dificultad: Moderada)
Es 2024, y hay cinco candidatos que se presentan a las primarias demócratas: Taylor Swift, Oprah Winfrey, Mark Cuban, Keanu Reeves y Dwayne Johnson. (Oye, podría pasar.) Como siempre, las primeras primarias son en Iowa.
En un esfuerzo por superar su bochorno tras la debacle de los caucus de 2020, el Partido Demócrata de Iowa acaba de anunciar una nueva forma infalible de encontrar al mejor candidato: habrá cuatro elecciones consecutivas.
Primero, el candidato 1 se enfrentará al candidato 2. A continuación, el ganador de ésta se enfrentará al candidato 3, luego ese ganador se enfrentará al candidato 4 y, finalmente, el ganador de esa elección se enfrentará al último candidato. Por la propiedad transitiva, el ganador de esta última elección debe ser el mejor candidato… así lo dice el Partido Demócrata de Iowa.
El candidato Keanu se ha sentido bastante decaído, ya que sabe que está clasificado casi al final por la mayoría de los votantes, y al principio por ninguno. De hecho, sabe que la población de Iowa se divide en cinco grupos iguales, y que sus preferencias son las siguientes:

Keanu es amigo de la infancia de Bill S. Preston, Esq., el nuevo jefe del Partido Demócrata de Iowa. Preston, seguro de que el orden de los candidatos no importa para el resultado, le dice a Keanu que puede elegir el orden de votación de los candidatos.
Entonces, ¿qué orden debe elegir Keanu?
Pista
¿Cómo le iría a Keanu en las carreras de uno a uno contra cada candidato?
Solución
¿Listo para la solución? Pincha aquí para ver si aciertas.
¿Quién ha abierto todas estas malditas taquillas?
(Dificultad: Moderada)
Hay 100 taquillas que se alinean en el pasillo principal del instituto Chelm. Cada noche, el director de la escuela se asegura de que todas las taquillas estén cerradas para que haya un comienzo ordenado al día siguiente. Un día, 100 traviesos estudiantes deciden que van a gastar una broma.
Todos los alumnos se reúnen antes de empezar las clases y se ponen en fila. El primer alumno recorre el pasillo y abre todas las taquillas. El siguiente estudiante le sigue cerrando todas las demás taquillas (empezando por la segunda). El alumno 3 va a cada tercera taquilla (empezando por la tercera) y la abre si está cerrada, y la cierra si está abierta. El estudiante 4 sigue abriendo cada cuarta taquilla si está cerrada y cerrándola si está abierta. Así sucesivamente hasta que el alumno 100 llega a la centésima taquilla. Cuando la directora llega más tarde por la mañana, ¿qué taquillas encuentra abiertas?
Pista
Asegúrate de prestar atención a todos los factores.
Solución
¿Listo para la solución? Haz clic aquí para ver si has acertado.