8.4 De Clausius-Clapeyron Vergelijking

Volgende: 8.5 Rankine-krachtkringlopen Up: 8. Krachtkringlopen Previous: 8.3 De Carnot-cyclus Inhoudsopgave Index

Tot nu toe hebben we alleen ideale gassen beschouwd en we willen laten zien dat de eigenschappen , enz. ware toestandsvariabelen zijn en dat de 1e en 2e wet van de thermodynamica gelden wanneer het werkmedium geen ideaal gas is (d.w.z. een tweefasig medium). Een elegante manier om dit te doen is een Carnot-cyclus te beschouwen voor een tweefasig medium.Het feit dat alle Carnot-motoren die werken tussen twee gegeven temperaturen hetzelfde rendement hebben, is een manier om de2e wet van de thermodynamica te stellen. De werkvloeistof behoeft geen ideaal gas te zijn en kan een van fase veranderend tweefasig medium zijn.

Het idee is om een Carnotmotor te laten draaien tussen temperaturen en voor een tweefasig medium en het een verandering van fase te laten ondergaan. We kunnen dan een belangrijk verband afleiden dat bekend staat als de vergelijking van Clausius en Clapeyron, die de helling van de dampdrukcurve geeft. We kunnen dan de dampdrukcurve voor verschillende stoffen meten en de gemeten helling vergelijken met de vergelijking van Clausius-Clapeyron. Dit kan dan worden gezien als een experimenteel bewijs van de algemene geldigheid van de 1e en 2e wet van de thermodynamica!

Figuur 8.8:Carnot-cyclus bedacht om de geldigheid van de wetten van de thermodynamica te testen

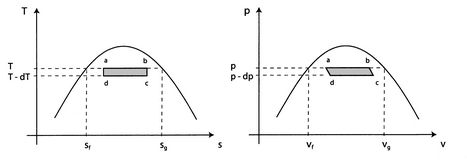
Overweeg de infinitesimale Carnot-cyclus die in figuur 8.8 wordt getoond. Er wordt warmte geabsorbeerd tussen de toestanden en . Om een willekeurige hoeveelheid massa te laten verdampen, , is de hoeveelheid warmte

(8…1)

moet aan het systeem worden toegevoerd. Uit de 1e en 2e wet van de thermodynamica kan het thermisch rendement voor een Carnot-cyclus worden geschreven als

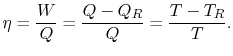Hieruit volgt, voor de hierboven beschouwde infinitesimale cyclus,

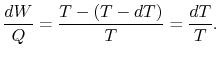(8..2)

De arbeid langs en bijna elkaar opheffen zodat het netto werk het verschil is tussen het werk langs en , en kan worden gezien als het gebied omsloten door de rechthoek :


	(8..3)

Samenvoeging van vergelijkingen (8.1) en(8.3) in (8.2) eenobtains

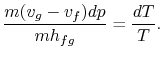Herrangschikking van termen levert de Clausius-Clapeyron vergelijking,die de helling van de dampdrukcurve bepaalt:

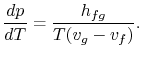(8..4)

Het mooie is dat we een algemene relatie hebben gevonden tussen proefondervindelijk meetbare grootheden uit eerste beginselen (1e en 2e wet van de thermodynamica).

Om de relatie tussen Clausius en Clapeyron uit te zetten en te vergelijken met experimenteel gemeten dampspanningskrommen, moeten we Vergelijking (8.4) integreren. Daartoe moeten de verdampingswarmte en het soortelijk volume bekende functies van de temperatuur zijn. Dit is een belangrijk probleem in de fysische chemie, maar we zullen er hier niet verder op ingaan, behalve om te vermelden dat als

variaties in de verdampingswarmte kunnen worden verwaarloosd,
de dampfase wordt verondersteld een ideaal gas te zijn, en
het specifieke volume van de vloeistof klein is vergeleken met dat van de dampfase,

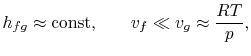de integratie kan gemakkelijk worden uitgevoerd8.1. Door deze benaderingen te maken, wordt de Clausius-Clapeyronequatie worden

Het uitvoeren van de integratie, de resulterende uitdrukking is

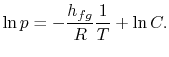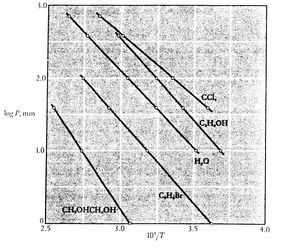
Merk op dat de dampdrukcurven rechte lijnen zijn als wordt uitgezet tegen en dat de helling van de curven, rechtstreeks verband houdt met de verdampingswarmte.De figuren 8.9, 8.9 en 8.22 geven de dampspanningskrommen voor verschillende stoffen weer. Het feit dat alle bekende stoffen in het twee-fasen gebied voldoen aan de vergelijking van Clausius-Clapeyron, bewijst de algemene geldigheid van de 1e en 2e wet van de thermodynamica!