Het toestandsruimtemodel van Lineair Tijds-Invariant (LTI) systeem kan worden voorgesteld als,
$=AX+BU$
$Y=CX+DU$
De eerste en de tweede vergelijking staan bekend als respectievelijk toestandsvergelijking en uitgangsvergelijking.
Waarbij,
-
X en $>ot{X}$ respectievelijk de toestandsvector en de differentiële toestandsvector zijn.
-
U en Y zijn respectievelijk de ingangsvector en de uitgangsvector.
-
A is de systeemmatrix.
-
B en C zijn de ingangs- en de uitgangsmatrices.
-
D is de feed-forward matrix.
Basisconcepten van het State Space Model
De volgende basisterminologie komt in dit hoofdstuk aan de orde.
State
Het is een groep variabelen, die de geschiedenis van het systeem samenvat om de toekomstige waarden (outputs) te kunnen voorspellen.
Statusvariabele
Het aantal benodigde toestandsvariabelen is gelijk aan het aantal opslagelementen dat in het systeem aanwezig is.
Voorbeelden – stroom door inductor, spanning over condensator
Statusvector
Het is een vector, die de toestandsvariabelen als elementen bevat.
In de eerdere hoofdstukken hebben we twee mathematische modellen van de regelsystemen besproken. Dat zijn het differentiaalvergelijkingsmodel en het overdrachtsfunctiemodel. Het toestandsruimtemodel kan worden verkregen uit een van deze twee wiskundige modellen. Laten we deze twee methoden nu een voor een bespreken.
State space model uit differentiaalvergelijking
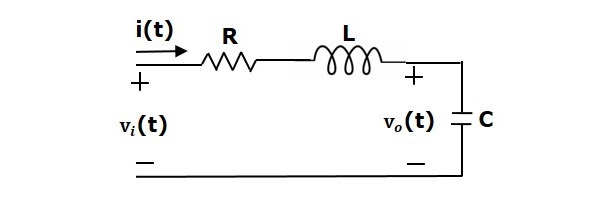
Er zijn twee opslagelementen (inductor en condensator) in deze schakeling. Het aantal toestandsvariabelen is dus gelijk aan twee en deze toestandsvariabelen zijn de stroom door de spoel, $i(t)$ en de spanning over de condensator, $v_c(t)$.
Vanuit de schakeling is de uitgangsspanning, $v_0(t)$ gelijk aan de spanning over de condensator, $v_c(t)$.
$v_0(t)=v_c(t)$
Toepassing van KVL rond de lus.
$v_i(t)=Ri(t)+L\frac{\text{d}i(t)}{\text{d}t}+v_c(t)$
$\frac{Ri(t)}{L}-\frac{v_c(t)}{L}+\frac{v_i(t)}{L}$
De spanning over de condensator is –
$v_c(t)=\frac{1}{C} \int i(t) dt$
Differentieer bovenstaande vergelijking naar de tijd.
$\frac{{d}v_c(t)}{{d}t}=\frac{i(t)}{C}$
Statusvector, $X=begin{bmatrix}i(t) \v_c(t) \eind{bmatrix}$
Differentiële toestandsvector, $\dot{X}=begin{bmatrix}\frac{\text{d}i(t)}{\text{d}t} \\\frac{\text{d}v_c(t)}{\text{d}t} \Einde{bmatrix}$
We kunnen de differentiaalvergelijkingen en de outputvergelijking in de standaardvorm van het toestandsruimtemodel ordenen als,
$Y={bmatrix}0 & 1 {bmatrix}{bmatrix}{bmatrix}i(t) \v_c(t) \end{bmatrix}$
Waar,
State Space Model from Transfer Function
Beschouw de twee typen transferfuncties op basis van het type termen dat in de teller aanwezig is.
- Overdrachtsfunctie met constante term in teller.
- Overdrachtsfunctie met polynomiale functie van ‘s’ in teller.
Overdrachtsfunctie met constante term in teller
Bedenk de volgende overdrachtsfunctie van een systeem
$\frac{Y(s)}{U(s)}=\frac{b_0}{s^n+a_{n-1}s^{n-1}+….+a_1s+a_0}$
Regregeer, bovenstaande vergelijking als
$(s^n+a_{n-1}s^{n-1}+…+a_0)Y(s)=b_0 U(s)$
Toep inverse Laplace-transformatie toe aan beide zijden.
$\frac{\text{d}^ny(t)}{\text{d}t^n}+a_{n-1}\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}+…+a_1\frac{\text{d}y(t)}{\text{d}t}+a_0y(t)=b_0 u(t)$
Let
$y(t)=x_1$
$\frac{\text{d}y(t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2y(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^ny(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then,
$\dot{x}_n+a_{n-1}x_n+…+a_1x_2+a_0x_1=b_0 u$
Vanuit bovenstaande vergelijking kunnen we de volgende toestandsvergelijking schrijven.
$$\dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+b_0 u$
De uitgangsvergelijking is –
$y(t)=y=x_1$
Het toestandsruimtemodel is –
De uitgangsvergelijking is –
$y(t)=y=x_1$
Het toestandsruimtemodel is -.
$\dot{X}=$\begin{bmatrix}\dot{x}_1 \\dot{x}_2 \\vdots \\dot{x}_{n-1} \\\dot{x}_n \eind{bmatrix}$
$Y=\begin{bmatrix}1 &&&& 0 \eind{bmatrix}\begin{bmatrix}x_1 \x_2 \\\vdots \x_{n-1} \x_n \eind{bmatrix}$
Hier, $D=links .
Voorbeeld
Vind het toestandsruimtemodel voor het systeem met overdrachtsfunctie.
$\frac{Y(s)}{U(s)}=\frac{1}{s^2+s+1}$
Reorganiseer bovenstaande vergelijking als,
$(s^2+s+1)Y(s)=U(s)$
Toepas aan beide zijden de inverse Laplace transformatie toe.
$\frac{{text{d}^2y(t)}{{text{d}t^2}+\frac{text{d}y(t)}{text{d}t}+y(t)=u(t)$
Let
$y(t)=x_1$
$\frac{{text{d}y(t)}{text{d}t}=x_2={x}_1$
en $u(t)=u$
Dan, is de toestandsvergelijking
$\dot{x}_2=-x_1-x_2+u$
De uitgangsvergelijking is
$y(t)=y=x_1$
Het toestandsruimtemodel is
$Y=\begin{bmatrix}1 & 0 \einde{bmatrix}\begin{bmatrix}x_1 \x_2 \einde{bmatrix}$
Overdrachtsfunctie met polynoomfunctie van ‘s’ in teller
Bedenk de volgende overdrachtsfunctie van een systeem
$$\frac{Y(s)}{U(s)}=\frac{b_n s^n+b_{n-1}s^{n-1}+…+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+…+a_1s+a_0}$
$Rightarrow \frac{Y(s)}{U(s)}=links( \frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1s+a_0}}}rechts )(b_n s^n+b_{n-1}s^{n-1}+….+b_1s+b_0)$
De bovenstaande vergelijking is in de vorm van product van overdrachtsfuncties van twee blokken, die gecascadeerd worden.
$\frac{Y(s)}{U(s)}=links(\frac{V(s)}{U(s)} \rechts ) \left(\frac{Y(s)}{V(s)} \rechts )$
Hier,
$\frac{V(s)}{U(s)}=\frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$
Regel bovenstaande vergelijking als
$(s^n+a_{n-1}s^{n-1}+…+a_0)V(s)=U(s)$
Toep inverse Laplace transform toe aan beide zijden.
$\frac{\text{d}^nv(t)}{\text{d}t^n}+a_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+…+a_1 \frac{\text{d}v(t)}{\text{d}t}+a_0v(t)=u(t)$
Let
$v(t)=x_1$
$\frac{\text{d}v((t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2v(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^nv(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then, is de toestandsvergelijking
$\dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+u$
Consider,
$\frac{Y(s)}{V(s)}=b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0$
Regregeer bovenstaande vergelijking als
$Y(s)=(b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0)V(s)$
Toepas aan beide zijden de inverse Laplace-transformatie toe.
$y(t)=b_n\frac{\text{d}^nv(t)}{\text{d}t^n}+b_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+…+b_1\frac{\text{d}v(t)}{\text{d}t}+b_0v(t)$
Door de toestandsvariabelen en $y(t)=y$ in bovenstaande vergelijking te substitueren, krijgt men de uitvoervergelijking als,
$y=b_n{x}_n+b_{n-1}x_n+…+b_1x_2+b_0x_1$
Substitueer, $\dot{x}_n$ waarde in de bovenstaande vergelijking.
$y=b_n(-a_0x_1-a_1x_2-…-a_{n-1}x_n+u)+b_{n-1}x_n+…+b_1x_2+b_0x_1$
$y=(b_0-b_na_0)x_1+(b_1-b_na_1)x_2+…+(b_{n-1}-b_na_{n-1})x_n+b_n u$
Het toestandsruimtemodel is
$\dot{X}=\begin{bmatrix}\dot{x}_1 \dot{x}_2 \vdots \dot{x}_{n-1} \\dot{x}_n \eind{bmatrix}$
$Y=\begin{bmatrix}x_1 \x_2 \\dot{x}_n-1} \x_n \eind{bmatrix}$
Als $b_n = 0$, dan
$Y=$begin{bmatrix}x_1 \x_2 \\vdots \x_{n-1} \x_n \eind{bmatrix}$