Heading

Just another blog

Binomiale verdeling

MathWorld Bijdragers > Yap >

DOWNLOAD Mathematica NotebookVERDER DIT ONDERWERP IN DE MathWorld-klasBinomialeDistributie

De binomiale verdeling geeft de discrete kansverdeling P_p(n|N) op het behalen van precies n successen uit N Bernoulli beproevingen (waarbij de uitkomst van elke Bernoulli beproeving waar is met kans p en onwaar met kans q=1-p). De binomiale verdeling wordt dus gegeven door

P_p(n|N) = (N; n)p^nq^(N-n)
(1)
= (N!)/(n!(N-n)!)p^n(1-p)^(N-n),
(2)

waar (N; n) een binomiaal coëfficiënt is. De bovenstaande plot toont de verdeling van n successen uit N=20 proeven met p=q=1/2.

De binomiale verdeling is in de Wolfram Language geïmplementeerd als BinomialDistribution.

De kans op meer successen dan de n die bij een binomiale verdeling wordt waargenomen, is

P=sum_(k=n+1)^N(N; k)p^k(1-p)^(N-k)=I_p(n+1,N-n),
(3)

waar

I_x(a,b)=(B(x;a,b))/(B(a,b)),
(4)

B(a,b) is de bètafunctie, en B(x;a,b) is de onvolledige bètafunctie.

De karakteristieke functie voor de binomiale verdeling is

phi(t)=(q+pe^(it))^N
(5)

(Papoulis 1984, p. 154). De moment-genererende functie M voor de verdeling is

M(t) = e^(tn)
(6)
= sum_(n=0)^(N)e^(tn)(N; n)p^nq^(N-n)
(7)
= sum_(n=0)^(N)(N; n)(pe^t)^n(1-p)^(N-n)
(8)
= ^N
(9)
M^'(t)'(t) = N^(N-1)(pe^t)
(10)
M^('')(t)'')(t) = N(N-1)^(N-2)(pe^t)^2+N^(N-1)(pe^t).
(11)

Het gemiddelde is

mu = M^'(0)'(0)
(12)
= N(p+1-p)p
(13)
= Np.
(14)

De momenten om 0 zijn

mu_1^'' = mu=Np
(15)
mu_2^'' = Np(1-p+Np)
(16)
mu_3^'' = Np(1-3p+3Np+2p^2-3Np^2+N^2p^2)
(17)
mu_4^'' = Np(1-7p+7Np+12p^2-18Np^2+6N^2p^2-6p^3+11Np^3-6N^2p^3+N^3p^3),
(18)

dus de momenten om het gemiddelde zijn

mu_2 = Np(1-p)=Npq
(19)
mu_3 = Np(1-p)(1-2p)
(20)
mu_4 = Np(1-p).
(21)

De skewness en kurtosisex zijn

gamma_1 = (1-2p)/(sqrt(Np(1-p))
(22)
= (q-p)/(sqrt(Npq))
(23)
gamma_2 = (6p^2-6p+1)/(Np(1-p))
(24)
= (1-6pq)/(Npq).
(25)

De eerste cumulant is

kappa_1=np,
(26)

en de daaropvolgende cumulanten worden gegeven door de recurrenselatie

kappa_(r+1)=pq(dkappa_r)/(dp).
(27)

De gemiddelde afwijking wordt gegeven door

MD=sum_(k=0)^N|k-Np|(N; k)p^k(1-p)^(N-k).
(28)

Voor het speciale geval p=q=1/2, is dit gelijk aan

MD = 2^(-N)sum_(k=0)^(N)(N; k)|k-1/2N|
(29)
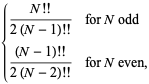= {(N!!)/(2(N-1)!!) voor N oneven; ((N-1)!)/(2(N-2)!!) voor N even,
(30)

waarbij N!! een dubbele factorial is. Voor N=1, 2, … zijn de eerste paar waarden dus 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, … (OEIS A086116 en A086117). Het algemene geval wordt gegeven door

MD=2(1-p)^(N-|_Np_|)p^(|_Np_|+1)(|_Np_|+1)(N; |_Np_|+1).
(31)

Steinhaus (1999, pp. 25-28) beschouwt het verwachte aantal vierkanten S(n,N,s) dat een gegeven aantal korrels n bevat op een bord met de grootte s na willekeurige verdeling van N korrels,

S(n,N,s)=sP_(1/s)(n|N).
(32)

Het nemen van N=s=64 levert de resultaten op die in de volgende tabel zijn samengevat.

n S(n,64,64)
0 23.3591
1 23.7299
2 11.8650
3 3.89221
2 11.8650
3 3.89221
3.89221
4 0.942162
5 0.179459
6 0.0280109
7 0.0280109
7 0.0036840
8 4.16639×10^(-4)
9 4.11495×10^(-5)
10 3.59242×10^(-6)

Een benadering van de binomiale verdeling voor grote N kan worden verkregen door uit te breiden over de waarde n^~ waar P(n) een maximum is, i.e., waarbij dP/dn=0. Aangezien de logaritmische functie monotoon is, kunnen we er ook voor kiezen de logaritme uit te breiden. Stel n=n^~+eta, dan

ln=ln+B_1eta+1/2B_2eta^2+1/(3!)B_3eta^3+...,
(33)

waar

B_k=)/(dn^k)]_(n=n^~).
(34)

Maar we zijn aan het uitbreiden over het maximum, dus, per definitie,

B_1=)/(dn)]_(n=n^~)=0.
(35)

Dit betekent ook dat B_2 negatief is, dus kunnen we B_2=-|B_2| schrijven. Als we nu de logaritme van (◇) nemen, krijgen we

ln=lnN!-lnn!-ln(N-n)!+nlnp+(N-n)lnq.
(36)

Voor grote n en N-n kunnen we de benadering van Stirling gebruiken

ln(n!) benadert nlnn-n,
(37)

zo

(d)/(dn) ca (lnn+1)-1
(38)
= lnn
(39)
(d)/(dn) ca d/(dn)
(40)
=
(41)
= -ln(N-n),
(42)

en

(dln)/(dn) ca -.lnn+ln(N-n)+lnp-lnq.
(43)

Om n^~ te vinden, stel je deze uitdrukking op 0 en los je op voor n,

ln((N-n^~)/(n^~)p/q)=0
(44)
(N-n^~)/(n^~)p/q=1
(45)
(N-n^~)p=n^~q
(46)
n^~(q+p)=n^~=Np,
(47)

sinds p+q=1. We kunnen nu de termen in de uitbreiding vinden

B_2 = )/(dn^2)]_(n=n^~)
(48)
= -1/(n^~)-1/(N-n^~)
(49)
= -1/(Npq)
(50)
= -1/(Np(1-p))
(51)
B_3 = )/(dn^3)]_(n=n^~)
(52)
= 1/(n^~^2)-= 1/(n^~^2)-iv1/((N-n^~)^2)
(53)
= (q^2-p^2)/(N^2p^2q^2)
(54)
= (1-2p)/(N^2p^2(1-p)^2)
(55)
B_4 = )/(dn^4)]_(n=n^~)
(56)
= -2/(n^~^3)-2/((n-n^~)^3)
(57)
= (2(p^2-pq+q^2))/(N^3p^3q^3)
(58)
= (2(3p^2-3p+1))/(N^3p^3(1-p)^3)).
(59)

BinomiaalGaussisch

Nu behandelen we de verdeling als continu,

lim_(N-infty)sum_(n=0)^NP(n) ca intP(n)dn=int_(-infty)^inftyP(n^~+eta)deta=1.
(60)

Omdat elke term van orde 1/N∼1/sigma^2 kleiner is dan de vorige, kunnen we termen hoger dan B_2 negeren, dus

P(n)=P(n^~)e^(-|B_2|eta^2/2).
(61)

De kans moet genormaliseerd worden, dus

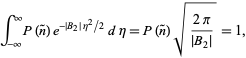int_(-infty)^inftyP(n^~)e^(-|B_2|eta^2/2)deta=P(n^~)sqrt((2pi)/(|B_2|))=1,
(62)

en

P(n) = sqrt((|B_2|)/(2pi))e^(-|B_2|(n-n^~)^2/2)
(63)
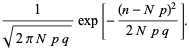= 1/(sqrt(2piNpq))exp.
(64)

Het definiëren van sigma^2=Npq,

P(n)=1/(sigmasqrt(2pi))exp,
(65)

wat een normale verdeling is. De binomiale verdeling wordt dus benaderd door een normale verdeling voor elke vaste p (zelfs als p klein is) als N op oneindig wordt gebracht.

Als N-infty en p-0 zo zijn dat Np-lambda, dan convergeert de binomiale verdeling naar de Poisson-verdeling met gemiddelde lambda.

Laat x en y onafhankelijke binomiale willekeurige variabelen zijn, gekarakteriseerd door parameters n,p en m,p. De voorwaardelijke kans op x gegeven dat x+y=k is

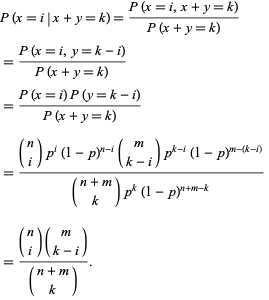P(x=i|x+y=k)=(P(x=i,x+y=k))/(P(x+y=k)) =(P(x=i,y=k-i))/(P(x+y=k)) =(P(x=i)P(y=k-i))/(P(x+y=k)) =((n; i)p^i(1-p)^(n-i)(m; k-i)p^(k-i)(1-p)^(m-(k-i)))/((n+m; k)p^k(1-p)^(n+m-k)) =((n; i)(m; k-i))/((n+m; k)).
(66)

Merk op dat dit een hypergeometrische verdeling is.

Geef een reactie

Het e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *