Als het aantal spleten in een obstakel groot is, wordt de scherpte van het patroon verbeterd en worden de maxima smaller. Obstakels met een groot aantal spleten (meer dan, zeg, 20 op de millimeter) worden diffractieroosters genoemd. Deze werden voor het eerst ontwikkeld door Fraunhofer aan het eind van de achttiende eeuw en zij bestonden uit fijn zilverdraad gewikkeld op twee parallelle schroeven, waardoor ongeveer 30 obstakels op de millimeter werden verkregen.
Sindsdien zijn er veel verbeteringen aangebracht; in 1882 gebruikte Rowland een diamant om fijne lijnen op glas te trekken, waarbij de ribbels als spleten fungeerden en de rulings als hindernissen (zie figuur 1). Met deze methode is het mogelijk diffractieroosters te verkrijgen met wel 3000 lijnen per millimeter, hoewel “grove” roosters met ongeveer 500 lijnen per millimeter beter zijn voor algemeen gebruik.
In veel scholen zijn twee typen in gebruik, één met 300 lijnen per mm en de andere met 80 lijnen per mm.
Reflectieroosters worden ook gebruikt, waarbij het verstrooide beeld wordt bekeken na reflectie van een geregelde oppervlakte. Een zeer goed voorbeeld van een reflectiediffractierooster is een CD. Een DVD met fijnere rulings geeft een veel breder diffractiepatroon.
De golftheorie en het diffractierooster
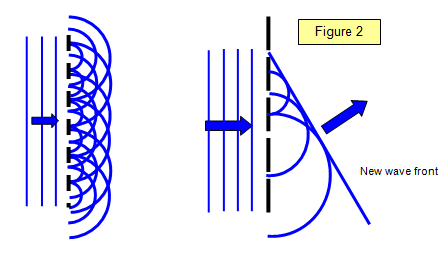
Figuur 2 toont de Huygens constructie voor een rooster. Je kunt zien hoe de cirkelvormige verstrooide golven van elke spleet zich in bepaalde richtingen bij elkaar optellen tot een verstrooide golf die een vlakke golffront heeft, net als de golven die het traliewerk van links raken. Deze vlakke golf wordt gevormd door de lijn te trekken die alle kleine cirkelvormige golven ontmoet en wordt een omhulsel van al deze kleine secundaire golven genoemd.
De diffractieroosterformule
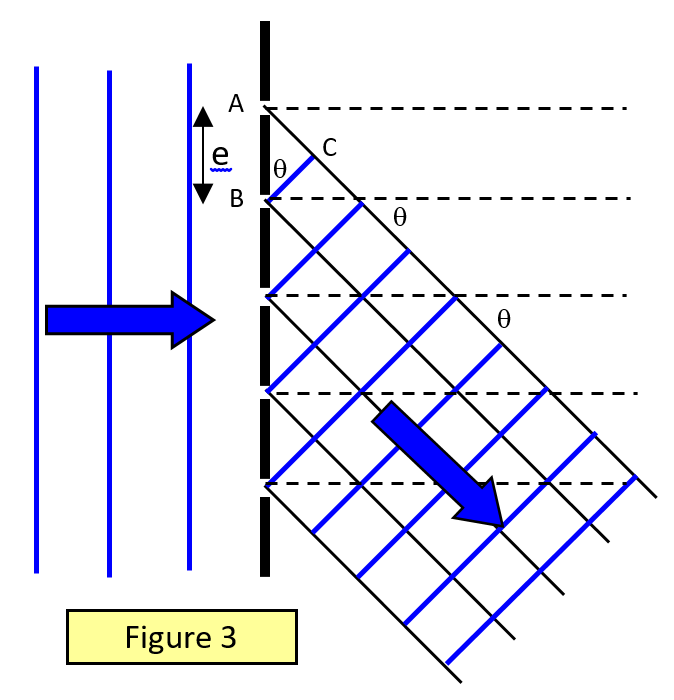
Bedenk een parallelle lichtstraal die normaal op een diffractierooster met een roosterafstand e valt (de roosterafstand is het omgekeerde van het aantal lijnen per lengte-eenheid). Beschouw licht dat wordt verstrooid onder een hoek q met de normaal en dat afkomstig is van overeenkomstige punten op aangrenzende tralies (figuur 3).
Voor een maximum is het wegverschil = AC = mλ
Maar AC = e sinθ. Daarom geldt voor een maximum:
mλ = e sinθ
waar m = 0, 1, 2,3….
Het getal m staat bekend als de orde van het spectrum, dat wil zeggen dat een spectrum van de eerste orde wordt gevormd voor m = 1, enzovoort.
Als licht van één golflengte wordt gebruikt, zoals dat van een laser, dan ontstaat een reeks scherpe lijnen, één lijn voor elke orde van het spectrum. Met een witte lichtbron wordt een reeks spectra gevormd, waarbij het licht van de kortste golflengte de kleinste buigingshoek heeft.
Bij het afleiden van de bovenstaande formule hebben we aangenomen dat de invallende straal loodrecht op het oppervlak van het tralie staat. Er moet rekening mee worden gehouden als dit niet het geval is. De eenvoudigste manier is om de positie van het spectrum van de eerste orde aan weerszijden van het centrum te meten, de hoek tussen deze posities te noteren en deze vervolgens te halveren, zoals getoond in figuur 4.
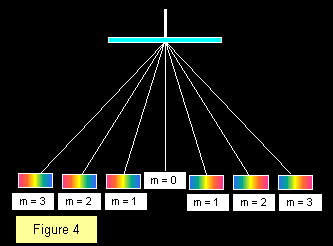
Het aantal spectraordes dat met een bepaalde tralie zichtbaar is, hangt af van de afstand tussen de tralies, waarbij meer spectra zichtbaar zijn bij grovere tralies. Het gestreepte oppervlak van de tralie moet altijd van het invallende licht af wijzen om fouten door richtingsveranderingen als gevolg van breking in het glas te voorkomen. Het diagram toont een centrale witte fringe met drie spectra aan weerszijden die in totaal zeven beelden geven.
(Zie voorbeeldopgave )
1. Bereken de golflengte van het monochromatische licht waarin het tweede orde beeld wordt verstrooid over een hoek van 25o met behulp van een diffractierooster met 300 lijnen per millimeter.
Roosterafstand (e) = 10-3/300 m = 3.3×10-6 m
Golflengte (l) = esin25/2 = /2 = 6,97×10-7 m = 697 nm
2. Bereken het maximaal aantal ordes dat zichtbaar is met een diffractierooster van 500 lijnen per millimeter, bij licht met een golflengte van 600 nm.
Maximale hoek van diffractie = 90o e = 10-3/500 = 2×10-6 m
Daaruit volgt m = esinq/l = 2×10-6/600×10-9 = 3,33
Daaruit volgt maximaal aantal ordes = 3, en zijn er in totaal zeven beelden van de bron te zien (drie aan elke kant van een centraal beeld).
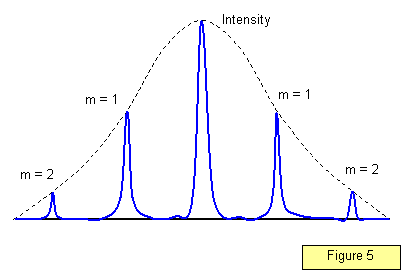
De intensiteitsverdeling in het diffractiepatroon voor een groot aantal spleten wordt getoond in figuur 5. Merk op dat de maxima veel scherper worden; hoe groter het aantal spleten per meter, des te beter gedefinieerd zijn de maxima.
De diffractie van cadmium- of kwiklicht wordt gebruikt om de scheiding van twee lijnen op een geïntegreerde schakeling te bepalen. De volgende resultaten zijn verkregen voor de tweede orde diffracties voor verschillende golflengten. Gebruik deze om een geschikte lineaire grafiek uit te zetten en vervolgens de gemiddelde afstand van de draden op de schakeling te bepalen.
| Wavelength/nm | Stralingshoek (o) |
| 468 | 28.0 |
| 480 | 28.7 |
| 509 | 31.0 |
| 546 | 33.0 |
| 577 | 35.5 |
| 644 | 40.0 |