De methode van Lagrange Multipliers is het werkpaard van de econoom voor het oplossen van optimalisatieproblemen. De techniek is een centraal onderdeel van de economische theorie, maar wordt helaas meestal slecht onderwezen.
De meeste leerboeken richten zich op het mechanisch uitdraaien van formules, waardoor studenten niet begrijpen waarom het eigenlijk werkt. In dit artikel leg ik een eenvoudige manier uit om te zien waarom Lagrange-vermenigvuldigers doen wat ze doen – namelijk het oplossen van beperkte optimalisatieproblemen met behulp van een halfmysterieuze Lagrangiaanse functie.
Enige achtergrond
Voordat je kunt zien waarom de methode werkt, moet je iets weten over gradiënten. Voor functies van één variabele is er – meestal – één eerste afgeleide. Voor functies van n variabelen zijn er n eerste afgeleiden. Een gradiënt is gewoon een vector die alle partiële eerste afgeleiden van de functie op één plaats verzamelt.
Elk element in de gradiënt is een van de partiële eerste afgeleiden van de functie. Een eenvoudige manier om aan een gradiënt te denken is dat, als we een punt op een functie kiezen, dit ons de “richting” geeft die de functie opgaat. Als onze functie is gelabeld
de notatie voor de gradiënt van f is
Het belangrijkste om te weten over gradiënten is dat ze altijd wijzen in de richting van de steilste helling van een functie op een gegeven punt. Kijk maar eens naar de onderstaande tekening om dit te illustreren. Het illustreert hoe gradiënten werken voor een twee-variabele functie van x1 en x2.
De functie f in de tekening vormt een heuvel. Naar de top toe heb ik twee gebieden getekend waar we de hoogte van f constant houden op een niveau a. Dit worden niveaucurven van f genoemd, en ze zijn gemarkeerd met f = a1, en f = a2.
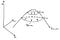
Stel je voor dat je op een van die vlakke bochten staat. Denk aan een wandelpad op een berghelling. Als je op het pad staat, in welke richting is de berg dan het steilst? Het is duidelijk dat de steilste richting recht omhoog is, loodrecht op het pad. In de tekening zijn deze steilste stijgingen met pijlen aangegeven. Dit zijn de stijgingspercentages
op verschillende punten langs de vlakke bochten. Net zoals de steilste wandeltocht altijd loodrecht op ons pad staat, staan de hellingen van f altijd loodrecht op de vlakke krommen.
Dat is het kernidee hier: vlakke krommen zijn waar
en
Hoe de methode werkt
Om te zien hoe Lagrange-vermenigvuldigers werken, kijk dan eens naar de tekening hieronder. Ik heb de functie f van hierboven opnieuw getekend, samen met een beperking g = c. In de tekening is de beperking een vlak dat onze heuvel doorsnijdt. Ik heb ook een paar vlakke krommen van f getekend.

Het doel is om zo hoog mogelijk op de heuvel te klimmen, aangezien we niet hoger kunnen komen dan waar de beperking g = c de heuvel snijdt.
In de tekening is de grens waar de beperking de functie snijdt met een dikke lijn aangegeven. Langs die lijn liggen de hoogste punten die we kunnen bereiken zonder over onze beperking heen te stappen. Dat is een voor de hand liggende plaats om te beginnen met zoeken naar een beperkt maximum.
Stel je voor dat we van links naar rechts lopen op de lijn van de beperking. Als we hoger komen, lopen we door verschillende niveaukrommen van f. Ik heb er twee aangegeven in het plaatje. Stel je voor dat je bij elke kromme de helling bekijkt – dat is de helling van een raaklijn eraan – en die vergelijkt met de helling op de beperking waar we nu staan.
Als onze helling groter is dan de kromme, kunnen we een hoger punt op de heuvel bereiken als we naar rechts blijven gaan. Als onze helling kleiner is dan de niveaulijn – bijvoorbeeld naar rechts waar onze beperkingslijn afneemt – moeten we naar links terug om een hoger punt te bereiken.
Als we een punt bereiken waar de helling van de beperkingslijn precies gelijk is aan de helling van de niveaulijn, zijn we zo hoog als we kunnen gekomen. Dat wil zeggen, we hebben ons beperkte maximum bereikt. Elke beweging vanaf dat punt zal ons naar beneden brengen. In de figuur is dit punt aangegeven met een grote pijl die naar de top wijst.
Op dat punt hebben de niveaukromme f = a2 en de beperking dezelfde helling. Dat betekent dat ze evenwijdig zijn en in dezelfde richting wijzen. Maar zoals we hierboven zagen, staan hellingen altijd loodrecht op vlakke krommen. Dus als deze twee krommen evenwijdig zijn, moeten hun hellingen ook evenwijdig zijn.
Dat betekent dat de hellingen van f en g beide in dezelfde richting wijzen, en ten hoogste een scalar verschillen. Laten we die scalair “lambda” noemen. Dan hebben we,
Oplossen voor nul, krijgen we
Dit is de voorwaarde die moet gelden wanneer we het maximum van f hebben bereikt onder de restrictie g = c. Als we slim zijn, kunnen we een enkele vergelijking schrijven die dit idee weergeeft. Dit is waar de bekende Lagrangiaanse vergelijking om de hoek komt kijken:
of nog explicieter,
Om te zien hoe deze vergelijking werkt, kijken we wat er gebeurt als we de gebruikelijke Lagrangiaanse procedure volgen. Eerst vinden we de drie partiële eerste afgeleiden van L,
en stel ze gelijk aan nul. Dat wil zeggen, we moeten de gradiënt van L gelijkstellen aan nul. Om de gradiënt van L te vinden, nemen we de drie partiële afgeleiden van L ten opzichte van x1, x2 en lambda. Dan plaatsen we ze elk als een element in een 3 x 1 vector. Dat geeft ons het volgende:
Bedenk dat we hier twee “regels” moeten volgen. Ten eerste moeten de hellingen van f en g in dezelfde richting wijzen, of
En ten tweede moeten we voldoen aan onze restrictie, of
Het eerste en tweede element van de gradiënt van L zorgen ervoor dat de eerste regel wordt gevolgd. Dat wil zeggen, ze dwingen
zodat de gradiënten van f en g beide in dezelfde richting wijzen. Het derde element van de gradiënt van L is gewoon een truc om ervoor te zorgen dat g = c, wat onze beperking is. Wanneer we in de Lagrangiaanse functie de partiële afgeleide ten opzichte van lambda nemen, krijgen we gewoon onze oorspronkelijke dwangvergelijking terug.
Op dit punt hebben we drie vergelijkingen in drie onbekenden. Dus kunnen we dit oplossen voor de optimale waarden van x1 en x2 die f maximaliseren onder onze beperking. En we zijn klaar.
Het komt er dus op neer dat Lagrange multipliers eigenlijk gewoon een algoritme is dat zoekt waar de gradiënt van een functie in dezelfde richting wijst als de gradiënten van zijn beperkingen, terwijl ook aan die beperkingen wordt voldaan.
Zoals met de meeste gebieden van de wiskunde, als je eenmaal tot de bodem gaat – in dit geval, dat optimalisatie eigenlijk gewoon heuvelklimmen is, wat iedereen begrijpt – zijn de dingen een stuk eenvoudiger dan de meeste economen doen voorkomen.