Heading

Keer terug naar de lessenindex | Doe de lessen op volgorde | Printvriendelijke pagina

Factorialen

Factorialen zijn heel eenvoudige dingen. Het zijn gewoon producten, aangegeven met een uitroepteken. Bijvoorbeeld, “vier factorial” wordt geschreven als “4!” en betekent 1×2×3×4 = 24. In het algemeen betekent n! (“enn factorieel”) het product van alle gehele getallen van 1 tot n; dat wil zeggen, n! = 1×2×3×…×n.

(Om verschillende redenen is 0! gedefinieerd als gelijk aan 1, niet 0. Onthoud dit nu: 0! = 1.)

• Bereken 6!.

1×2×3×4×5×6 = 720

Veel (de meeste?) rekenmachines kunnen factorials voor je berekenen. Het commando factorial is bijvoorbeeld beschikbaar in het menu “kansberekening” op een van mijn rekenmachines:

Zoek naar een ” ! “knop, of kijk in de handleiding.

• Vergelijk 12! Copyright © Elizabeth Stapel 2004-2011 Alle rechten voorbehouden

12! = 1×2×3×4×… Oh, wat maakt het ook uit. Waar is mijn rekenmachine…?



12! = 479001600

Als je combinaties, permutaties en kansberekening gaat doen, zul je uitdrukkingen moeten vereenvoudigen die factorialen in de tellers en de noemers hebben. Bijvoorbeeld:

• Vergenvoudig de volgende:

Ik kan dit doen in mijn rekenmachine:

Ik kan ook werken vanuit de definitie van een factorie:



In beide gevallen is 6! ÷ 4! = 30

Zie hoe ik in het vorige probleem een heleboel getallen heb kunnen wegstrepen. Dit komt door de manier waarop factorialen zijn gedefinieerd, en deze eigenschap kan je werk een stuk vereenvoudigen.

• Versimpel het volgende:

Meteen kan ik de factoren 1 tot en met 14 die zowel bij 17! als bij 14! voorkomen, elimineren. Dan kan ik wat overblijft vereenvoudigen en krijg ik:

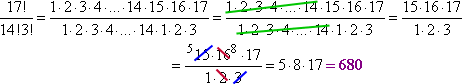
Zie hoe ik heb ingekort wat ik moest schrijven door een gat (de “ellipsis”, of driedubbele punt) in het midden te laten. Dit proces van gat-en-annuleren zal later handig zijn (zoals bij wiskunde, waar je deze techniek veel zult gebruiken), vooral wanneer je te maken hebt met uitdrukkingen die je rekenmachine niet aankan. Bijvoorbeeld:

• Versimpel het volgende:

Mijn rekenmachine kan dit niet voor me berekenen, omdat ik te maken heb met variabelen in plaats van getallen. Ik zal dit met de hand moeten vereenvoudigen. Om dit te doen, zal ik de factorialen uitschrijven, waarbij ik genoeg van de factoren gebruik om dingen te hebben die kunnen opheffen. Terugdenkend aan “getal”-woordproblemen liggen opeenvolgende gehele getallen een eenheid uit elkaar, dus de factoren in het product (n + 2)! zijn van de vorm:

1×2×3×4×…×(n – 1)×(n)×(n + 1)×(n + 2)

Door terug te gaan in de lijst van factoren tot aan “n – 1”, heb ik een lijst van factoren gemaakt die kunnen opheffen:

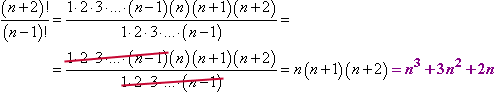
Let op de manier waarop ik met die annulering ben omgegaan. Ik heb de factoriële uitdrukkingen zo uitgebreid dat ik kon zien waar ik dubbele factoren kon opheffen. Ook al had ik geen idee wat n zou kunnen zijn, ik kon nog steeds annuleren. Berg deze techniek op in je geheugen, want zelfs als je hem nu niet nodig hebt, zul je hem later vrijwel zeker nodig hebben.

Voor informatie over het vinden van het aantal nullen aan het eind van een factoriaal (zoals “Hoeveel nullen staan er op het eind van 23! nadat je het hebt vermenigvuldigd?”), kijk dan eens naar deze notitie.

Top | Terug naar index

Citeer dit artikel als:

Stapel, Elizabeth. “Factorials.” Purplemath. Beschikbaar via https://www.purplemath.com/modules/factorial.htm. Toegankelijk 2016