Leerdoelen
Aan het eind van dit deel zul je in staat zijn:
- Niet-conservatieve krachten te definiëren en uit te leggen hoe ze mechanische energie beïnvloeden.
- laten zien hoe het principe van behoud van energie kan worden toegepast door de conservatieve krachten te behandelen in termen van hun potentiële energieën en alle niet-conservatieve krachten in termen van de arbeid die ze verrichten.
Niet-conservatieve krachten en wrijving
Krachten zijn ofwel conservatief ofwel niet-conservatief. Conservatieve krachten zijn besproken in Conservatieve krachten en potentiële energie. Een niet-conservatieve kracht is een kracht waarbij de arbeid afhangt van de afgelegde weg. Wrijving is een goed voorbeeld van een niet-conservatieve kracht. Zoals geïllustreerd in figuur 1 hangt de arbeid die tegen wrijving wordt verricht af van de lengte van de weg tussen het begin- en eindpunt. Vanwege deze afhankelijkheid van het traject is er geen potentiële energie verbonden aan niet-conservatieve krachten. Een belangrijk kenmerk is dat de arbeid verricht door een niet-conservatieve kracht mechanische energie aan een systeem toevoegt of onttrekt. Wrijving, bijvoorbeeld, creëert thermische energie die dissipeert, waardoor energie aan het systeem wordt onttrokken. Bovendien, zelfs als de thermische energie wordt vastgehouden of gevangen, kan zij niet volledig in arbeid worden omgezet, zodat zij ook in die zin verloren gaat of niet kan worden teruggewonnen.

Figuur 1. De hoeveelheid van het gelukkige gezichtje dat wordt uitgegumd hangt af van de weg die de gum tussen de punten A en B aflegt, evenals de arbeid die tegen de wrijving in wordt verricht. Er wordt minder werk verricht en er wordt minder van het gezichtje uitgewist voor het pad in (a) dan voor het pad in (b). De kracht hier is wrijving, en het grootste deel van de arbeid gaat in thermische energie die vervolgens het systeem verlaat (het gelukkige gezicht plus het gummetje). De verbruikte energie kan niet volledig worden teruggewonnen.
Hoe niet-conservatieve krachten de mechanische energie beïnvloeden
Mechanische energie wordt mogelijk niet behouden wanneer niet-conservatieve krachten werken. Wanneer bijvoorbeeld een auto op een vlakke ondergrond door wrijving tot stilstand wordt gebracht, verliest hij kinetische energie, die als thermische energie wordt afgevoerd, waardoor zijn mechanische energie afneemt. In figuur 2 worden de effecten van conservatieve en niet-conservatieve krachten vergeleken. Vaak kiezen we ervoor eerst eenvoudiger systemen te begrijpen, zoals dat in figuur 2a, voordat we ingewikkelder systemen bestuderen, zoals in figuur 2b.

Figuur 2. Vergelijking van de effecten van conservatieve en niet-conservatieve krachten op de mechanische energie van een systeem. (a) Een systeem met alleen conservatieve krachten. Wanneer een steen op een veer valt, blijft de mechanische energie constant (zonder rekening te houden met de luchtweerstand) omdat de kracht in de veer conservatief is. De veer kan de steen terugstuwen naar zijn oorspronkelijke hoogte, waar hij weer alleen potentiële energie heeft door de zwaartekracht. (b) Een systeem met niet-conservatieve krachten. Wanneer dezelfde steen op de grond valt, wordt hij tegengehouden door niet-conservatieve krachten die zijn mechanische energie afvoeren in de vorm van thermische energie, geluid en vervorming van het oppervlak. De steen heeft mechanische energie verloren.
Hoe de Werk-Energiestelling van toepassing is
Laten we nu eens kijken hoe de Werk-Energiestelling eruit ziet als er zowel conservatieve als niet-conservatieve krachten werken. We zullen zien dat de arbeid verricht door niet-conservatieve krachten gelijk is aan de verandering in de mechanische energie van een systeem. Zoals vermeld in Kinetische energie en het werk-energietheorema, stelt het werk-energietheorema dat de netto arbeid van een systeem gelijk is aan de verandering in zijn kinetische energie, of Wnet = ΔKE. De netto arbeid is de som van de arbeid door niet-conservatieve krachten plus de arbeid door conservatieve krachten. Dat wil zeggen,
Wnet = Wnc + Wc,
zoals
Wnc + Wc = ΔKE,
waarbij Wnc de totale arbeid is van alle niet-conservatieve krachten en Wc de totale arbeid van alle conservatieve krachten.

Figuur 3. Een persoon duwt een krat een helling op en verricht daarbij arbeid op de krat. Wrijving en zwaartekracht (niet weergegeven) werken ook op de krat; beide krachten werken de duwkracht van de persoon tegen. Als de krat de helling op wordt geduwd, wint hij aan mechanische energie, wat betekent dat de arbeid van de persoon groter is dan de arbeid van de wrijving.
Bekijk figuur 3, waarin een persoon een krat een helling op duwt en daarbij wordt tegengewerkt door wrijving. Net als in het vorige hoofdstuk stellen we vast dat de arbeid van een conservatieve kracht voortkomt uit een verlies van gravitatiepotentiaal, zodat Wc = -ΔPE. Substitueren van deze vergelijking in de vorige en oplossen voor Wnc geeft
Wnc = ΔKE + ΔPE.
Deze vergelijking betekent dat de totale mechanische energie (KE + PE) verandert met precies de hoeveelheid arbeid die door niet-conservatieve krachten wordt verricht. In figuur 3 is dit de arbeid verricht door de persoon minus de arbeid verricht door wrijving. Dus zelfs als de energie niet behouden blijft voor het systeem waar het om gaat (zoals de krat), weten we dat een gelijke hoeveelheid arbeid is verricht om de verandering in de totale mechanische energie te veroorzaken.
We herschikken Wnc = ΔKE + ΔPE om
KEi + PEi + Wnc = KEf + PEf te verkrijgen.
Dit betekent dat de hoeveelheid werk die door niet-conservatieve krachten wordt verricht, bijdraagt aan de mechanische energie van een systeem. Als Wnc positief is, neemt de mechanische energie toe, zoals wanneer de persoon de krat op de helling in figuur 3 duwt. Als Wnc negatief is, dan is de mechanische energie afgenomen, zoals wanneer de steen de grond raakt in figuur 2b. Als Wnc nul is, dan blijft de mechanische energie behouden, en zijn de niet-conservatieve krachten in evenwicht. Als je bijvoorbeeld een grasmaaier met constante snelheid voortduwt op een vlakke ondergrond, wordt jouw verrichte arbeid tenietgedaan door de wrijvingsarbeid, en heeft de maaier een constante energie.
Toepassing van behoud van energie met niet-conservatieve krachten
Wanneer er geen verandering in de potentiële energie optreedt, komt de toepassing van KEi + PEi + Wnc = KEf + PEf neer op de toepassing van de werk-energietheorema door de verandering in kinetische energie gelijk te stellen aan de netto arbeid die op het systeem wordt uitgeoefend, wat in het meest algemene geval zowel conservatieve als niet-conservatieve krachten omvat. Maar als je in plaats daarvan een verandering in de totale mechanische energie wilt vinden in situaties waarin zowel potentiële als kinetische energie verandert, dan zegt de vorige vergelijking KE i + PEi + Wnc = KEf + PEf dat je kunt beginnen met de verandering in mechanische energie te vinden die zou zijn voortgekomen uit alleen de conservatieve krachten, inclusief de potentiële energieveranderingen, en daar de arbeid bij op te tellen, met het juiste teken, door alle betrokken niet-conservatieve krachten.
Voorbeeld 1. Berekening van de afgelegde afstand: Hoe ver een honkbalspeler glijdt
Bekijk de situatie in figuur 4, waarin een honkbalspeler op een vlakke ondergrond tot stilstand komt. Bereken met behulp van energieoverwegingen de afstand die de honkbalspeler van 65,0 kg aflegt, gegeven dat zijn beginsnelheid 6,00 m/s is en de wrijvingskracht tegen hem een constante 450 N is.

Figuur 4. De honkbalspeler glijdt tot stilstand over een afstand d. Daarbij verwijdert wrijving de kinetische energie van de speler door een hoeveelheid arbeid te verrichten die gelijk is aan de aanvankelijke kinetische energie.
Strategie
Wrijving brengt de speler tot stilstand door zijn kinetische energie om te zetten in andere vormen, waaronder thermische energie. In termen van de werk-energietheorie wordt de door wrijving verrichte arbeid, die negatief is, opgeteld bij de oorspronkelijke kinetische energie om deze tot nul te reduceren. De door wrijving verrichte arbeid is negatief, omdat f in de tegengestelde richting van de beweging is (dat wil zeggen, θ = 180º, en dus cos θ = -1). Dus Wnc = -fd. De vergelijking vereenvoudigt tot
frac{1}{2}{mv_{text{i}}^2-fd=0
of
fd=frac{1}{2}{mv_{text{i}}^2
.
Deze vergelijking kan nu worden opgelost voor de afstand d.
Oplossing
Oplossen van de vorige vergelijking voor d en substitueren van bekende waarden levert
begin{array}{lll}d&&\frac{mv_{\text{i}}^2}{2f}\\\text{ }&&\frac{(65.kg})(6.00{ m/s})^2}{(2)(450{ N})}&&2.60{array} m}
Discussie
Het belangrijkste punt van dit voorbeeld is dat de hoeveelheid niet-conservatieve arbeid gelijk is aan de verandering in mechanische energie. Je moet bijvoorbeeld harder werken om een vrachtwagen, met zijn grote mechanische energie, te stoppen dan om een mug te stoppen.
Voorbeeld 2. Berekening van de afgelegde afstand: Sliding Up an Incline
Voorstel dat de speler uit Voorbeeld 1 een heuvel op rent met een helling van 5,00º naar boven met een oppervlak vergelijkbaar met dat in het honkbalstadion. De speler glijdt met dezelfde beginsnelheid. Bepaal hoe ver hij glijdt.

Figuur 5. Dezelfde honkbalspeler glijdt tot stilstand op een helling van 5,00º.
Strategie
In dit geval vermindert de arbeid die door de niet-conservatieve wrijvingskracht op de speler wordt verricht, de mechanische energie die hij heeft van zijn kinetische energie op nul hoogte, tot de uiteindelijke mechanische energie die hij heeft door zich over afstand d voort te bewegen om hoogte h langs de helling te bereiken, met h = d sin 5,00º. Dit wordt uitgedrukt door de vergelijking KE + PEi + Wnc = KE f + PEf.
Oplossing
De door wrijving verrichte arbeid is weer Wnc = -fd; de potentiële energie is aanvankelijk PEi = mg – 0 = 0 en de kinetische energie is \text{KE}_{text{i}}=\frac{1}{2}mv_{text{i}^2}; de uiteindelijke energiebijdragen zijn KEf = 0 voor de kinetische energie en PEf = mgh = mgd sin θ voor de potentiële energie.
Substitueren van deze waarden geeft
{1}{2}{mv_{text{i}}}^2+0+{emv_{text{i}}}^2+0+{emv}(-fd(-rechts)=0+mgd(-)(-theta)
Oplos dit voor d om
begin{array}{lll}d&&\frac{\left(\frac{1}{2}\right)mv_{\text{i}}^2}{f+mg\sin\theta}\\&&\frac{(0.5)(65.0 kg})(6.00 m/s})^2}{450 N}+(65.0 kg})links(9.80 m/s}^2rechts)sinus(5.00^circ})}&&2.31{m}
Discussie
Zoals te verwachten was, glijdt de speler een kortere afstand door bergopwaarts te glijden. Merk op dat het probleem ook opgelost had kunnen worden in termen van de directe krachten en de arbeidsenergietheorie, in plaats van gebruik te maken van de potentiële energie. Deze methode zou hebben vereist dat de vectoren van de normaalkracht en de zwaartekracht, die elkaar niet meer opheffen omdat ze in verschillende richtingen wijzen, en de wrijving worden gecombineerd om de netto kracht te vinden. Met behulp van de netto kracht en de netto arbeid zou men dan de afstand d kunnen vinden die de kinetische energie tot nul terugbrengt. Door behoud van energie toe te passen en in plaats daarvan de potentiële energie te gebruiken, hoeven we alleen de gravitationele potentiële energie mgh te beschouwen, zonder de krachtvectoren te combineren en op te lossen. Dit vereenvoudigt de oplossing aanzienlijk.
Het leggen van verbanden: Take-Home Investigation-Determining Friction from the Stopping Distance
Dit experiment betreft de omzetting van gravitationele potentiële energie in thermische energie. Gebruik de liniaal, het boek en de knikker uit het onderdeel “Verbanden leggen” van Gravitationele potentiële energie. Daarnaast heb je een schuimrubberen beker nodig met een klein gaatje in de zijkant, zoals te zien is in figuur 6. Laat de knikker vanaf de 10-cm-positie op de liniaal in de beker rollen die onderaan de liniaal staat. Meet de afstand d het kopje beweegt voordat het tot stilstand komt. Welke krachten zorgden ervoor dat de knikker tot stilstand kwam? Wat gebeurde er met de kinetische energie van de knikker onder aan de liniaal? Plaats vervolgens de knikker op de 20-cm en de 30-cm positie en meet opnieuw de afstand die de beker beweegt nadat de knikker erin is gevallen. Zet de afstand die het kopje aflegt uit tegen de oorspronkelijke positie van de knikker op de liniaal. Is dit verband lineair?
Met enkele eenvoudige aannamen kun je deze gegevens gebruiken om de kinetische wrijvingscoëfficiënt μk van het kopje op de tafel te vinden. De wrijvingskracht f op het kopje is μkN, waarbij de normaalkracht N gewoon het gewicht van het kopje plus de knikker is. De normaalkracht en de zwaartekracht verrichten geen arbeid omdat zij loodrecht staan op de verplaatsing van het kopje, dat horizontaal beweegt. De door wrijving verrichte arbeid is fd. Je hebt de massa van de knikker ook nodig om de initiële kinetische energie te berekenen.
Het is interessant om het bovenstaande experiment ook uit te voeren met een stalen knikker (of kogellager). Laat je deze knikker los van dezelfde posities op de liniaal als je deed met de glazen knikker, is de snelheid van deze stalen knikker dan gelijk aan de snelheid van de knikker onder aan de liniaal? Is de afstand die de beker aflegt evenredig met de massa van de stalen en glazen knikker?

Figuur 6. Een knikker over een liniaal in een beker van schuim laten rollen.
PhET Verkenningen: De helling
Ontdek krachten, energie en arbeid terwijl je huishoudelijke voorwerpen een helling op en af duwt. Laat de helling zakken en stijgen om te zien hoe de hellingshoek de parallelle krachten op de dossierkast beïnvloedt. Grafieken tonen krachten, energie en arbeid.
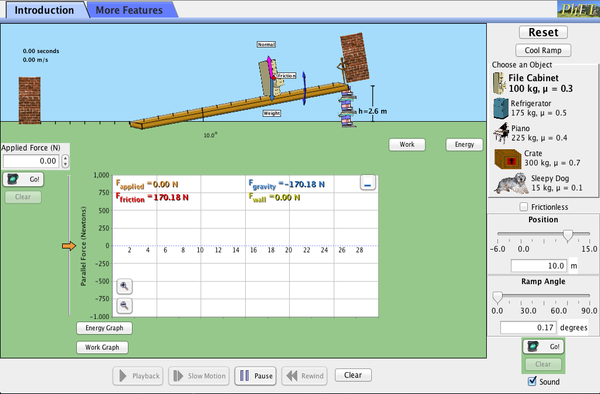
Klik om te downloaden. Uitvoeren met Java.
Sectiesamenvatting
- Een niet-conservatieve kracht is er een waarbij de arbeid afhangt van de weg.
- Wrijving is een voorbeeld van een niet-conservatieve kracht die mechanische energie in thermische energie verandert.
- Werk Wnc verricht door een niet-conservatieve kracht verandert de mechanische energie van een systeem. In de vorm van een vergelijking is Wnc = ΔKE + ΔPE of, omgekeerd, KEi + PEi + Wnc = KEf + PEf.
- Wanneer zowel conservatieve als niet-conservatieve krachten werken, kan behoud van energie worden toegepast en gebruikt om de beweging te berekenen in termen van de bekende potentiële energieën van de conservatieve krachten en de arbeid van de niet-conservatieve krachten, in plaats van de nettowerkzaamheid te vinden uit de nettokracht, of de wetten van Newton rechtstreeks toe te passen.
Problemen & Oefeningen
- Een skiester van 60,0 kg met een beginsnelheid van 12,0 m/s rolt een 2,50 m hoge helling op, zoals in figuur 7 is te zien. Bereken haar eindsnelheid op de top, gegeven dat de wrijvingscoëfficiënt tussen haar ski’s en de sneeuw 0,0800 is. (Hint: Bereken de afgelegde afstand op de helling uitgaande van een rechtlijnig pad zoals in de figuur.)

Figuur 7. De aanvankelijke kinetische energie van de skiër wordt gedeeltelijk gebruikt bij het uitrollen naar de top van een helling.
- (a) Hoe hoog kan een auto een helling oprollen (motor uitgeschakeld) als de door wrijving verrichte arbeid verwaarloosbaar is en de beginsnelheid 110 km/u bedraagt? b) Als in werkelijkheid wordt waargenomen dat een auto van 750 kg met een beginsnelheid van 110 km/u een heuvel oprijdt tot een hoogte van 22,0 m boven het beginpunt, hoeveel thermische energie werd dan opgewekt door wrijving? c) Wat is de gemiddelde wrijvingskracht als de heuvel een helling heeft van 2,5º boven het horizontale vlak?
Glossary
nonconservatieve kracht: een kracht waarvan de arbeid afhangt van het afgelegde traject tussen de gegeven begin- en eindconfiguraties
wrijving: de kracht tussen oppervlakken die zich verzet tegen het ene glijden over het andere; wrijving verandert mechanische energie in thermische energie
Selected Solutions to Problems & Oefeningen
1. 9,46 m/s