⇐ Vorig onderwerp|Next onderwerp ⇒ Inhoudsopgave
Voordat u een experiment uitvoert, moet u een vermogensanalyse uitvoeren om het aantal waarnemingen te schatten dat u nodig hebt om een goede kans te hebben het effect waarnaar u op zoek bent te detecteren.
Inleiding
Wanneer u een experiment ontwerpt, is het een goed idee om de steekproefgrootte te schatten die u nodig zult hebben. Dit geldt vooral als je voorstelt iets pijnlijks te doen met mensen of andere gewervelde dieren, waarbij het bijzonder belangrijk is het aantal individuen te minimaliseren (zonder de steekproefgrootte zo klein te maken dat het hele experiment een verspilling van tijd en lijden is), of als je een zeer tijdrovend of duur experiment plant. Voor veel statistische tests zijn methoden ontwikkeld om de steekproefgrootte te schatten die nodig is om een bepaald effect te detecteren, of om de grootte te schatten van het effect dat met een bepaalde steekproefgrootte kan worden gedetecteerd.
Om een poweranalyse te kunnen doen, moet je een effectgrootte specificeren. Dit is de grootte van het verschil tussen uw nulhypothese en de alternatieve hypothese die u hoopt te detecteren. Voor toegepast en klinisch biologisch onderzoek kan er een heel precieze effectgrootte zijn die je wilt detecteren. Als u bijvoorbeeld een nieuwe hondenshampoo test, kan de marketingafdeling van uw bedrijf u vertellen dat het produceren van de nieuwe shampoo alleen de moeite waard zou zijn als de vacht van honden er gemiddeld ten minste 25% glanzender door zou worden. Dat zou uw effectgrootte zijn, en u zou die gebruiken om te beslissen hoeveel honden u door de hondenreflectometer moet laten gaan.
Bij fundamenteel biologisch onderzoek weet u vaak niet hoe groot het verschil is waarnaar u op zoek bent, en de verleiding kan groot zijn om gewoon de grootste steekproefgrootte te gebruiken die u zich kunt veroorloven, of een steekproefgrootte te gebruiken die vergelijkbaar is met ander onderzoek op uw gebied. Je zou toch een power analyse moeten doen voor je het experiment uitvoert, gewoon om een idee te krijgen van het soort effecten dat je zou kunnen detecteren. Sommige anti-vaccinatie gekken hebben bijvoorbeeld voorgesteld dat de Amerikaanse regering een groot onderzoek uitvoert onder ongevaccineerde en gevaccineerde kinderen om te zien of vaccins autisme veroorzaken. Het is niet duidelijk welke effectgrootte interessant zou zijn: 10% meer autisme in één groep? 50% meer? Twee keer zoveel? Uit een power-analyse blijkt echter dat zelfs als alle niet-gevaccineerde kinderen in de Verenigde Staten van 3 tot 6 jaar en een gelijk aantal gevaccineerde kinderen in de studie zouden worden opgenomen, er 25% meer autisme in één groep zou moeten zijn om een grote kans te hebben een significant verschil te zien. Een meer plausibele studie, van 5.000 niet-gevaccineerde en 5.000 gevaccineerde kinderen, zou een significant verschil met hoge power alleen aantonen als er in de ene groep drie keer zoveel autisme zou zijn als in de andere. Omdat het onwaarschijnlijk is dat er zo’n groot verschil in autisme is tussen gevaccineerde en ongevaccineerde kinderen, en omdat het niet vinden van een verband met zo’n studie de anti-vaccinatie kooks niet zou overtuigen dat er geen verband is (niets zou hen overtuigen dat er geen verband is – dat is wat hen kooks maakt), vertelt de power analyse je dat zo’n grote, dure studie niet de moeite waard zou zijn.
Parameters
Er zijn vier of vijf getallen betrokken bij een power analyse. U moet de waarden voor elk van deze getallen kiezen voordat u de analyse uitvoert. Als u geen goede reden hebt om een bepaalde waarde te gebruiken, kunt u verschillende waarden proberen en kijken naar het effect op de steekproefgrootte.
Effectgrootte
De effectgrootte is de minimale afwijking van de nulhypothese die u hoopt te detecteren. Als u bijvoorbeeld hennen behandelt met iets waarvan u hoopt dat het de geslachtsverhouding van hun kuikens verandert, kunt u besluiten dat de minimale verandering in de verhouding tussen de geslachten waarnaar u zoekt 10% is. Je zou dan zeggen dat je effectgrootte 10% is. Als je iets test om de kippen meer eieren te laten leggen, is de effectgrootte misschien 2 eieren per maand.
Soms heb je een goede economische of klinische reden om een bepaalde effectgrootte te kiezen. Als je een voedingssupplement voor kippen test dat $1,50 per maand kost, wil je alleen weten of het meer dan $1,50 aan extra eieren per maand oplevert; weten dat een supplement 0,1 ei per maand extra oplevert, is geen nuttige informatie voor je, en je hoeft je experiment niet te ontwerpen om dat te weten te komen. Maar voor het meeste fundamenteel biologisch onderzoek is de effectgrootte gewoon een mooi rond getal dat je uit je kont hebt getrokken. Laten we zeggen dat je een power analyse doet voor een studie van een mutatie in een promotor regio, om te zien of het de genexpressie beïnvloedt. Hoe groot is de verandering in genexpressie waar je naar op zoek bent: 10%? 20%? 50%? Het is een vrij willekeurig getal, maar het zal een enorm effect hebben op het aantal transgene muizen die hun dure kleine leven zullen geven voor uw wetenschap. Als u geen goede reden hebt om naar een bepaalde effectgrootte te zoeken, kunt u dat net zo goed toegeven en een grafiek tekenen met steekproefgrootte op de X-as en effectgrootte op de Y-as. G*Power doet dit voor u.
Alpha
Alpha is het significantieniveau van de test (de P-waarde), de kans dat de nulhypothese wordt verworpen ook al is die waar (een vals-positief). De gebruikelijke waarde is alpha=0.05. Sommige power calculators gebruiken de eenstaart-alfa, wat verwarrend is, aangezien de tweestaart-alfa veel gebruikelijker is. Zorg ervoor dat u weet welke u gebruikt.
Beta of power
Beta is in een poweranalyse de kans dat de nulhypothese wordt aanvaard, ook al is deze vals (vals-negatief), wanneer het echte verschil gelijk is aan de minimale effectgrootte. De power van een test is de kans dat de nulhypothese wordt verworpen (een significant resultaat wordt verkregen) wanneer het werkelijke verschil gelijk is aan de minimale effectgrootte. De power is 1-bèta. Er is geen duidelijke consensus over de te gebruiken waarde, dus ook dit is een getal dat je uit je mouw trekt; een power van 80% (gelijk aan een beta van 20%) is waarschijnlijk het meest gebruikelijk, terwijl sommige mensen 50% of 90% gebruiken. De kosten van een fout-negatief moeten je keuze beïnvloeden; als je echt, echt zeker wilt zijn dat je je effectgrootte detecteert, zul je een hogere waarde voor power (lagere beta) willen gebruiken, wat zal resulteren in een grotere steekproefgrootte. Sommige power calculators vragen je om bèta in te voeren, terwijl andere vragen om power (1-bèta); zorg ervoor dat je goed begrijpt welke je moet gebruiken.
Standaardafwijking
Voor meetvariabelen hebt u ook een schatting van de standaardafwijking nodig. Als de standaardafwijking groter wordt, wordt het moeilijker om een significant verschil te ontdekken, dus heb je een grotere steekproefgrootte nodig. Je schatting van de standaardafwijking kan komen van pilotexperimenten of van vergelijkbare experimenten in de gepubliceerde literatuur. Het is onwaarschijnlijk dat uw standaardafwijking precies hetzelfde is als u het experiment uitvoert, dus uw experiment zal in feite iets krachtiger of minder krachtig zijn dan u had voorspeld.
Voor nominale variabelen is de standaardafwijking een eenvoudige functie van de steekproefgrootte, dus u hoeft deze niet apart te schatten.
Hoe het werkt
De details van een power-analyse zijn verschillend voor verschillende statistische tests, maar de basisconcepten zijn vergelijkbaar; hier zal ik de exacte binomiale test als voorbeeld gebruiken. Stel je voor dat je polsbreuken bestudeert, en je nulhypothese is dat de helft van de mensen die een pols breken hun rechterpols breken, en de andere helft hun linkerpols. U besluit dat de minimale effectgrootte 10% is; als het percentage mensen dat hun rechterpols breekt 60% of meer is, of 40% of minder, dan wilt u een significant resultaat uit de exact binomiale toets. Ik heb geen idee waarom je 10% hebt gekozen, maar dat is wat je zult gebruiken. Alpha is 5%, zoals gewoonlijk. Je wilt 90% power, wat betekent dat als het percentage gebroken rechter polsen echt 40% of 60% is, je een steekproefgrootte wilt die 90% van de tijd een significant (P<0.05) resultaat oplevert, en slechts 10% van de tijd een niet-significant resultaat (wat in dit geval een vals negatief zou zijn).
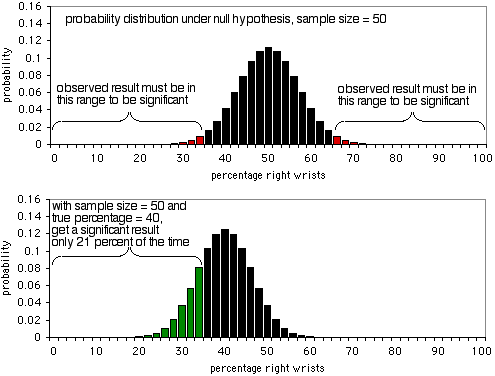

De eerste grafiek toont de kansverdeling onder de nulhypothese, met een steekproefgrootte van 50 individuen. Als de nulhypothese waar is, zal ongeveer 5% van de tijd minder dan 36% of meer dan 64% van de mensen hun rechterpols breken (een vals-positief). Zoals de tweede grafiek laat zien, als het ware percentage 40% is, zullen de steekproefgegevens slechts 21% van de tijd minder dan 36 of meer dan 64% zijn; u zou slechts 21% van de tijd een ware positieve uitslag krijgen, en 79% van de tijd een valse negatieve uitslag. Het is duidelijk dat een steekproefgrootte van 50 te klein is voor dit experiment; het zou slechts 21% van de tijd een significant resultaat opleveren, zelfs als er een 40:60 verhouding is tussen gebroken rechter- en linkerpols.
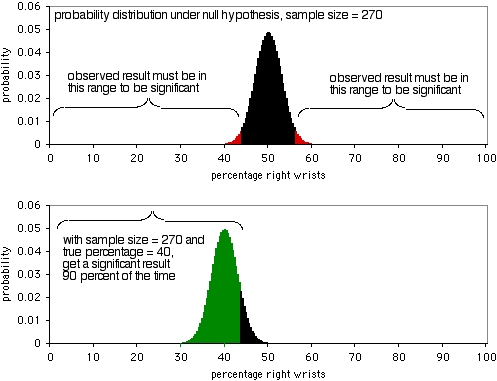

De volgende grafiek toont de kansverdeling onder de nulhypothese, met een steekproefgrootte van 270 individuen. Om significant te zijn op het P<0,05-niveau, zou het waargenomen resultaat minder dan 43,7% of meer dan 56,3% van de mensen moeten zijn die hun rechterpols breken. Zoals de tweede grafiek laat zien, als het werkelijke percentage 40% is, zullen de steekproefgegevens 90% van de tijd zo extreem zijn. Een steekproefgrootte van 270 is vrij goed voor dit experiment; het zou 90% van de tijd een significant resultaat opleveren als er een verhouding van 40:60 is tussen gebroken rechter- en linkerpols. Als de verhouding tussen gebroken rechter- en linkerpols verder weg ligt van 50:50, heb je een nog grotere kans op een significant resultaat.
Voorbeelden
Je bent van plan erwten te kruisen die heterozygoot zijn voor de kleur geel/groen, waarbij geel dominant is. De verwachte verhouding in de nakomelingen is 3 geel: 1 groen. U wilt weten of gele erwten daadwerkelijk meer of minder fit zijn, wat zich zou kunnen uiten in een andere verhouding gele erwten dan verwacht. U besluit willekeurig dat u een steekproefgrootte wilt die een significant (P<0,05) verschil detecteert als er 3% meer of minder gele erwten zijn dan verwacht, met een power van 90%. U toetst de gegevens met de exacte binomiale goodness-of-fit test als de steekproefgrootte klein genoeg is, of met een G-test of goodness-of-fit als de steekproefgrootte groter is. De power-analyse is voor beide tests hetzelfde.
Gebruik makend van G*Power zoals beschreven voor de exacte goodness-of-fit test, is het resultaat dat je 2109 erwtenplanten nodig hebt om 90% van de tijd een significant (P<0,05) resultaat te krijgen, als het werkelijke aandeel gele erwten 78% is, en 2271 erwten als het werkelijke aandeel 72% geel is. Omdat je geïnteresseerd bent in een afwijking in beide richtingen, gebruik je het grotere getal, 2271. Dat zijn veel erwten, maar u bent gerustgesteld dat het geen belachelijk aantal is. Als u een verschil van 0,1% tussen het verwachte en het waargenomen aantal gele erwten wilt detecteren, kunt u uitrekenen dat u 1.970.142 erwten nodig hebt; als dat is wat u moet detecteren, vertelt de steekproefgrootte-analyse u dat u een erwtensorteerrobot in uw budget moet opnemen.
De voorbeeldgegevens voor de tweesample t-toets laten zien dat de gemiddelde lengte in de sectie Biologische gegevensanalyse van 14.00 uur 66,6 centimeter was en de gemiddelde lengte in de sectie van 17.00 uur 64,6 centimeter, maar het verschil is niet significant (P=0,207). U wilt weten hoeveel leerlingen u moet bemonsteren om 80% kans te hebben dat zo’n groot verschil significant is. Voer met G*Power, zoals beschreven op de pagina over de twee-monsters t-test, 2,0 in voor het verschil in gemiddelden. Bereken met behulp van de STDEV-functie in Excel de standaardafwijking voor elke steekproef in de oorspronkelijke gegevens; deze is 4,8 voor steekproef 1 en 3,6 voor steekproef 2. Voer 0,05 in voor alpha en 0,80 voor power. Het resultaat is 72, wat betekent dat als de leerlingen van 17.00 uur echt 5 cm korter zijn dan de leerlingen van 14.00 uur, je in elke klas 72 leerlingen nodig hebt om 80% van de tijd een significant verschil te ontdekken, als het echte verschil echt 5 cm is.
Hoe doe je power-analyses
G*Power
G*Power is een uitstekend gratis programma, beschikbaar voor Mac en Windows, waarmee je power-analyses kunt maken voor een grote verscheidenheid aan tests. Ik zal uitleggen hoe je G*Power kunt gebruiken voor power analyses voor de meeste testen in dit handboek.
R
Salvatore Mangiafico’s R Companion heeft voorbeeld R-programma’s om power-analyses te doen voor veel van de tests in dit handboek; ga naar de pagina voor de individuele test en scroll naar beneden voor het power-analyse programma.
SAS
SAS heeft een PROC POWER die je kunt gebruiken voor power-analyses. Je voert de benodigde parameters in (die variëren afhankelijk van de test) en voert een periode in (die in SAS missing data symboliseert) voor de parameter waarvoor je een oplossing zoekt (meestal ntotal, de totale steekproefgrootte, of npergroup, het aantal monsters in elke groep). Ik vind dat G*Power voor dit doel gemakkelijker te gebruiken is dan SAS, dus ik raad niet aan om SAS te gebruiken voor je power-analyses.
⇐ Vorig onderwerp|Volgende onderwerp ⇒ Inhoudsopgave
Deze pagina is voor het laatst herzien op 20 juli 2015. Het adres ervan is http://www.biostathandbook.com/power.html. It may be cited as:
McDonald, J.H. 2014. Handbook of Biological Statistics (3e ed.). Sparky House Publishing, Baltimore, Maryland. Deze webpagina bevat de inhoud van pagina 40-44 in de gedrukte versie.
©2014 door John H. McDonald. U kunt waarschijnlijk doen wat u wilt met deze inhoud; zie de toestemmingspagina voor details.