Wat is een interkwartielafstand?
De interkwartielafstand is een maat voor waar de “middelste vijftig” in een gegevensverzameling ligt. Een interkwartielafstand geeft aan waar het begin en het eind van een reeks zich bevinden, terwijl een interkwartielafstand aangeeft waar het grootste deel van de waarden ligt. Daarom wordt bij de rapportage van bijvoorbeeld schoolprestaties of SAT-scores de voorkeur gegeven aan de interkwartielafstand boven veel andere spreidingsmaten.
De formule voor de interkwartielafstand is het eerste kwartiel verminderd met het derde kwartiel:
Inhoud (klik om naar het paginagedeelte te gaan):
Oplossen met de hand:
- Oplos de formule met de hand (oneven reeks getallen).
- Wat als ik een even reeks getallen heb?
- Vind een interkwartielafstand voor een oneven reeks getallen: Tweede methode
- Box Plot interkwartiel bereik: Hoe het te vinden
Technologie gebruiken:
- Interkwartielbereik in Minitab
- Interkwartielbereik in Excel
- Interkwartielbereik in SPSS
- Interkwartielbereik op de TI83
- Q1, Q3 en de IQR op de TI89
Algemene info:
- Wat is een interkwartielafstand?
- Wat is de Interkwartielafstandformule?
- IQR als test voor normale verdeling
- Waarvoor wordt een Interkwartielafstand gebruikt?
- Geschiedenis van de Interkwartielafstand.
Oplos de formule met de hand.
Bekijk de video of lees de stappen hieronder. Als je nog steeds moeite hebt, kijk dan eens naar de docenten op Chegg.com. De eerste 30 minuten zijn gratis.
Stappen:
- Stap 1: Zet de getallen op volgorde.
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27. - Stap 2: Zoek de mediaan.
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27. - Stap 3: Zet haakjes rond de getallen boven en onder de mediaan.
Statistisch gezien niet nodig, maar het maakt Q1 en Q3 gemakkelijker te herkennen.
(1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27). - Stap 4: Vind Q1 en Q3
Denk aan Q1 als een mediaan voor de onderste helft van de gegevens en denk aan Q3 als een mediaan voor de bovenste helft van de gegevens.
(1, 2, 5, 6, 7), 9, ( 12, 15, 18, 19, 27). Q1 = 5 en Q3 = 18. - Stap 5: Trek Q1 van Q3 af om de interkwartielafstand te vinden.
18 – 5 = 13.
Vindt u de uitleg goed? Kijk dan eens in het Practisch Spieken Handboek Statistiek, met nog honderden andere stap-voor-stapuitleg, net als deze!
Wat als ik een even reeks getallen heb?
Voorbeeldvraag: Vind de IQR voor de volgende dataset: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
- Stap 1: Zet de getallen op volgorde.
3, 5, 7, 8, 9, 11, 15, 16, 20, 21. - Stap 2: Maak een markering in het midden van de gegevens:
3, 5, 7, 8, 9, | 11, 15, 16, 20, 21. - Stap 3: Zet haakjes rond de getallen boven en onder de markering die je in Stap 2 hebt gemaakt, dat maakt Q1 en Q3 makkelijker te zien.
(3, 5, 7, 8, 9), | (11, 15, 16, 20, 21). - Stap 4: Zoek Q1 en Q3
Q1 is de mediaan (het midden) van de onderste helft van de gegevens, en Q3 is de mediaan (het midden) van de bovenste helft van de gegevens.
(3, 5, 7, 8, 9), | (11, 15, 16, 20, 21). Q1 = 7 en Q3 = 16. - Stap 5: Trek Q1 af van Q3.
16 – 7 = 9.
Dit is je IQR.
Terug naar boven
Een interkwartielafstand vinden voor een oneven reeks getallen: Alternatieve methode
Zoals u wellicht al weet, is niets “in steen gebeiteld” in de statistiek: wanneer sommige statistici een interkwartielafstand vinden voor een reeks oneven getallen, nemen zij de mediaan in beide kwartielen op. Bijvoorbeeld, in de volgende reeks getallen: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27 zouden sommige statistici het in twee helften breken, waarbij ze de mediaan (9) in beide helften opnemen:
(1, 2, 5, 6, 7, 9), (9, 12, 15, 18, 19, 27)
Dit leidt tot twee helften met een even reeks getallen, zodat je de bovenstaande stappen kunt volgen om de IQR te vinden.
Terug naar boven
De interkwartielafstand van de boxplot: Hoe vindt u het
Bekijk de video of lees de stappen hieronder:
Box Plot interkwartielafstand: Hoe deze te vinden
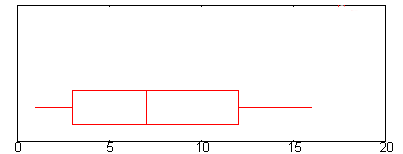

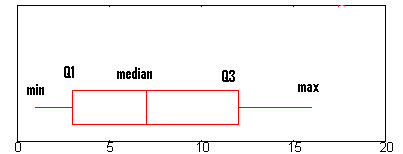
Voorbeeldvraag: Vind de interkwartielafstand voor de bovenstaande boxplot.
- Stap 1: Vind Q1.Q1 wordt weergegeven door de linkerrand van de “box” (op het punt waar de whisker stopt).
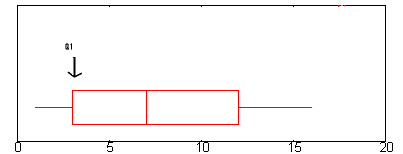
In de bovenstaande grafiek ligt Q1 ongeveer op 2,6. (Een volledige uitleg van Q1 staat hier: Het vijfgetallenoverzicht.)
- Stap 2: Vind Q3.
Q3 wordt op een boxplot weergegeven door de rechterrand van het “vakje”.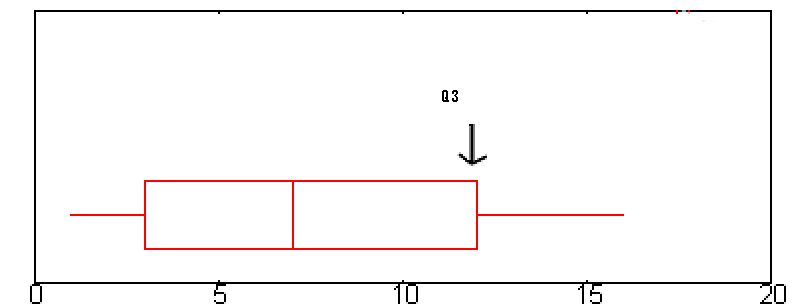
Q3 is ongeveer 12 in deze grafiek. - Stap 3: Trek het getal dat je in stap 1 hebt gevonden af van het getal dat je in stap 3 hebt gevonden.
Dit geeft je de interkwartielafstand. 12 – 2,6 = 9,4.
Dat is het!
Terug naar boven
Interquartile Range in Minitab
Lees verder voor stap-voor-stap aanwijzingen, of bekijk de video-versie hieronder.
Interquartile Range in Minitab: Stappen
Voorbeeldvraag: Vind een interkwartielafstand in Minitab voor het Grade Point Average (GPA) in de volgende gegevensverzameling:
Grade Point Average (GPA): 1(3,2), 1(3,1), 2(3,5), 2(2,0), 3(1.9), 3(4.0), 3(3.9), 4(3.8), 4(2.9), 5(3.9), 5(3.2), 5(3.3), 6(3.4), 6(2.6), 6(2.5), 7(2.0), 7(1.5), 8(4.0), 8(2.0).
Stap 1: Typ uw gegevens in een Minitab-werkblad. Voer uw gegevens in één of twee kolommen in.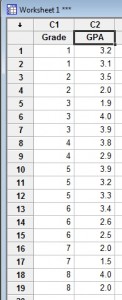
Stap 2: Klik op “Statistieken”, klik vervolgens op “Basisstatistieken” en klik vervolgens op “Beschrijvende statistische gegevens weergeven” om het menu Beschrijvende statistische gegevens te openen.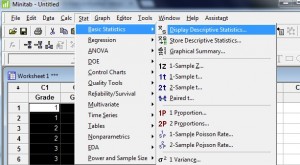
Stap 3: Klik op de naam van een variabele in het linkervenster en klik vervolgens op de knop “Selecteren” om de naam van de variabele over te brengen naar het rechtervenster.
Stap 4: Klik op de knop “Statistieken”.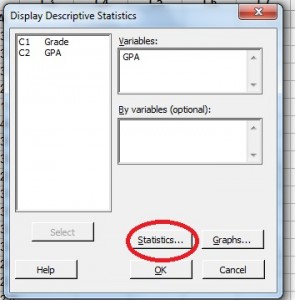
Stap 5: Vink “Interkwartiel bereik.”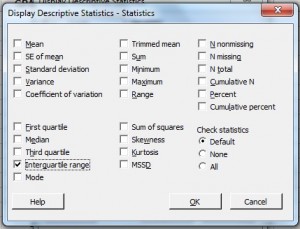 .
.
Step 6: Klik op de knop “OK” (een nieuw venster wordt geopend met het resultaat). De IQR voor de GPA in deze specifieke dataset is 1,8.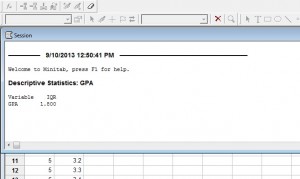
Dat is het!
Tip: Als u geen beschrijvende statistieken in een venster ziet, klik dan op “Venster” op de werkbalk en vervolgens op “Tegelen”. Klik op het venster Session (dit is waar beschrijvende statistische gegevens verschijnen) en scroll vervolgens omhoog om uw resultaten te zien.
Terug naar boven
Hoe een interkwartielbereik te vinden Excel 2007
Bekijk de video of lees de onderstaande stappen om een interkwartielbereik te vinden in Excel 2007:
Stappen:
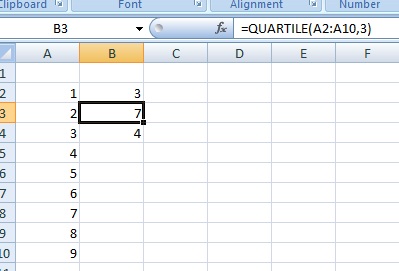
Stap 1: Typ uw gegevens in een enkele Excel kolom op een werkblad. Typ uw gegevens bijvoorbeeld in de cellen A2 tot en met A10. Laat geen gaten in je gegevens.
Stap 2: Klik op een lege cel (bijvoorbeeld, klik op cel B2) en typ dan =QUARTILE(A2:A10,1). U moet A2:A10 vervangen door de werkelijke waarden uit uw gegevensverzameling. Als u bijvoorbeeld uw gegevens in B2 tot B50 hebt getypt, is de vergelijking =QUARTILE(B2:B50,1). De “1” in deze Excel formule(A2:A10,1) vertegenwoordigt het eerste kwartiel (d.w.z. het punt dat op 25% van de gegevensverzameling ligt).
Stap 3: Klik op een tweede lege cel (bijvoorbeeld, klik op cel B3) en typ vervolgens =QUARTILE(A2:A10,3). Vervang A2:A10 door de werkelijke waarden uit uw gegevensverzameling. De “3” in deze Excel formule (A2:A10,3) vertegenwoordigt het derde kwartiel (d.w.z. het punt dat op 75% van de gegevensverzameling ligt).
Stap 4: Klik op een derde lege cel (bijvoorbeeld, klik op cel B4) en typ vervolgens =B3-B2. Als uw kwartielfuncties uit stap 2 en 3 zich op verschillende locaties bevinden, wijzigt u de celverwijzingen.
Stap 5: Druk op de “Enter”-toets. Excel geeft de IQR terug in de cel waarop u in stap 4 hebt geklikt
Dat is het!
Terug naar boven
Hoe vindt u een interkwartielbereik in SPSS
Zoals de meeste technologie, heeft SPSS verschillende manieren waarop u de IQR kunt berekenen. Als u echter klikt op de meest intuïtieve manier waarop u die zou verwachten te vinden (“Descriptive Statistics > Frequencies”), is de verrassing dat de IQR niet wordt vermeld (hoewel het eerste, tweede en derde kwartiel wel worden vermeld). U zou deze route kunnen volgen en dan het derde kwartiel van het eerste kunnen aftrekken om de IQR te krijgen. De gemakkelijkste manier om het interkwartielbereik in SPSS te vinden is echter met het commando “Verkennen”. Als u al gegevens in uw werkblad hebt getypt, sla dan stap 3 over.
Bekijk de video of lees de stappen hieronder:
Stappen
Stap 1: Open een nieuw gegevensbestand in SPSS. Klik op “Bestand”, ga met de muis over “Nieuw” en klik dan op “Gegevens”.
Stap 2: Typ uw gegevens in kolommen in het werkblad. U kunt zoveel kolommen gebruiken als u nodig hebt, maar laat geen lege rijen of spaties tussen uw gegevens. Zie: How to Enter Data into SPSS.
Step 3: Klik op “Analyze,” en ga dan met de muis over “Descriptive Statistics.” Klik op “Verkennen” om het dialoogvenster “Verkennen” te openen.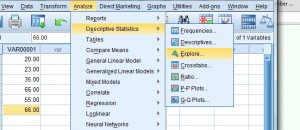
Stap 4: Klik op de naam van de variabele (dat is gewoon een mooie naam voor de kolomkop), klik vervolgens op de bovenste pijl om de variabele naar het vak “Afhankelijke lijst” te verplaatsen.
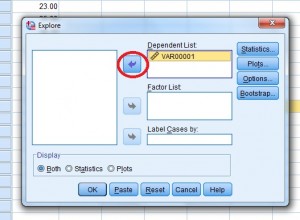
Het dialoogvenster “Variabelen verkennen”.
Step 5: Klik op “OK.” Het interkwartielbereik wordt vermeld in het vak Beschrijvingen.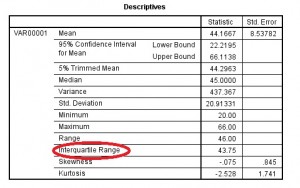
Tip: In dit voorbeeld is slechts één lijst in het gegevensblad getypt, maar het is mogelijk dat u uit meerdere lijsten kunt kiezen, afhankelijk van de manier waarop u uw gegevens hebt ingevoerd. Zorg ervoor dat u de juiste variabele (kolomnamen) selecteert voordat u verder gaat. Indien u meer gedenkwaardige variabele namen wenst, verander dan de kolomtitel door te klikken op de knop “variabele bekijken” helemaal onderaan links op het werkblad. Typ uw nieuwe variabele naam en ga dan terug naar de gegevensweergave door op de knop “gegevensweergave” te klikken.
Terug naar boven
Wat is een interkwartielafstand?
Stel u alle gegevens in een verzameling voor als punten op een getallenlijn. Als u bijvoorbeeld 3, 7 en 28 in uw gegevensverzameling hebt, stelt u zich die voor als punten op een getallenlijn die gecentreerd is op 0 maar zich zowel oneindig onder nul als oneindig boven nul uitstrekt. Eenmaal uitgezet op die getallenlijn vormen het kleinste gegevenspunt en het grootste gegevenspunt in de gegevensverzameling de grenzen (d.w.z. een ondergrens en een bovengrens) van een ruimte-interval op de getallenlijn dat alle gegevenspunten in de verzameling bevat. De interkwartielafstand (IQR) is de lengte van de middelste 50% van dat ruimte-interval.
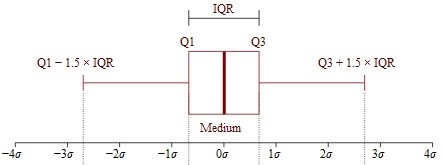
De interkwartielafstand is de middelste 50% van een gegevensreeks. Box and whiskers image by Jhguch at en.wikipedia
Als u wilt weten wat de IQR in formele termen is, wordt de IQR berekend als: Het verschil tussen het derde of bovenste kwartiel en het eerste of onderste kwartiel. Kwartiel is een term die wordt gebruikt om aan te geven hoe de gegevensverzameling in vier gelijke porties wordt verdeeld (denk aan kwartiel).
IQR-voorbeeld
Als u een verzameling hebt met de gegevenspunten 1, 3, 5, 7, 8, 10, 11 en 13, is het eerste kwartiel 4, het tweede kwartiel 7,5 en het derde kwartiel 10,5. Teken deze punten op een getallenlijn en u zult zien dat deze drie getallen de getallenlijn verdelen in kwartielen van 1 tot 13. Het IQR van die gegevensverzameling is dus 6,5, berekend als 10,5 min 4. Het eerste en derde kwartiel worden ook wel het 25e en 75e percentiel genoemd, omdat dat de equivalente getallen zijn wanneer de gegevensverzameling in procenten in plaats van kwartalen wordt verdeeld.
Terug naar boven
Interkwartielbereik met de TI83
Bekijk de video of lees de stappen hieronder:
Hoewel je de handige online interkwartielbereik-calculator op deze website kunt gebruiken, is dat misschien geen optie bij een test of toets. De meeste docenten staan het gebruik van een TI-83 bij toetsen toe, en het is zelfs een van de weinige rekenmachines die bij het AP-examen Statistiek is toegestaan. Het vinden van de TI 83 interkwartielafstand is niet meer dan het invoeren van uw datalijst en het drukken op een paar knoppen.
Voorbeeldopgave: Vind de TI 83 interkwartielafstand voor de hoogtes van de top 10 gebouwen in de wereld (per 2009). De hoogtes, (in voet) zijn: 2717, 2063, 2001, 1815, 1516, 1503, 1482, 1377, 1312, 1272.
Stappen
Stap 1: Voer de bovenstaande gegevens in een lijst op de TI 83 rekenmachine in. Druk op de STAT-toets en vervolgens op ENTER. Voer het eerste getal (2717) in en druk dan op ENTER. Ga door met het invoeren van getallen en druk na elke invoer op ENTER.
Stap 2: Druk op de STAT-toets.
Stap 3: Druk op de pijltoets naar rechts (de pijltoetsen bevinden zich rechtsboven op het toetsenblok) om “Calc.”
Step 4: Druk op ENTER om “1-Var Stats” te markeren.”
Step 5: Druk nogmaals op ENTER om een lijst met stats op te roepen.
Step 6:Scroll met de pijltjestoetsen door de lijst om Q1 en Q3 te vinden. Schrijf die getallen op. Je zou de getallen kunnen kopiëren en plakken, maar helaas, Texas Instruments maakt dit niet gemakkelijk:
- Gebruik de pijltjestoetsen om de cursor aan het begin van de
tekst te plaatsen die je wilt markeren. - Gebruik het TI Keyboard, houd de Shift-toets ingedrukt, en gebruik dan de pijltjestoetsen om de tekst te markeren.
- Laat de Shift-toets en de pijltjestoets los.
Het menu Kopiëren en Plakken zou moeten verschijnen, zodat u de gegevens kunt kopiëren en plakken. U zou dit twee keer moeten doen (elke keer terugkeren naar het HOME scherm), dus het is veel sneller om de getallen gewoon op te schrijven.
Step 7:Trek Q1 af van Q3 om de IQR te vinden (strong>624 feet voor deze set getallen).
Dat is het!
Terug naar boven
Hoe vind je Q1, Q3 en de Interkwartielafstand TI 89
Bekijk de video of lees de stappen hieronder:
Voorbeeldprobleem: Vind Q1, Q3, en de IQR voor de volgende lijst getallen: 1, 9, 2, 3, 7, 8, 9, 2.
Stap 1: Druk op APPS. Blader naar Stats/List Editor (gebruik de pijltjestoetsen op het toetsenbord om te bladeren). Druk op ENTER. Als u niet beschikt over de stats/lijst editor kunt u deze hier downloaden.
Stap 2: Wis de lijst editor van gegevens: druk op F1 8.
Stap 3: Druk op ALPHA 9 ALPHA 1 ENTER. Dit geeft uw lijst de naam “IQ.”
Stap 4: Voer uw getallen in, een voor een. Druk na elke invoer op de ENTER-toets. Voor onze groep getallen voert u
1,9,2,3,7,8,9,2
Stap 5: Druk op F4 en vervolgens op ENTER (voor het 1-var-statenscherm).
Stap 6: Vertel de rekenmachine dat u statistieken wilt voor de lijst met de naam “IQ” door ALPHA 9 ALPHA 1 in te voeren in het vak “Lijst:”. De rekenmachine zou automatisch de cursor daar voor je moeten plaatsen. Druk tweemaal op ENTER.
Stap 7:Lees de resultaten. Q1 staat in de lijst als Q1X (in ons voorbeeld is Q1X=2). Q3 staat in de lijst als Q3X (Q3X=8,5). Om de IQR te vinden, trekt u Q1 af van Q3 op het beginscherm. De IQR is 8,5-2=6,5.
Dat is het!
Terug naar boven
Wat is de formule voor het interkwartielbereik?
De IQR-formule is:
IQR = Q3 – Q1
Waarbij Q3 het bovenste kwartiel is en Q1 het onderste kwartiel.
IQR als test voor normale verdeling
Gebruik de formule voor de interkwartielafstand met het gemiddelde en de standaardafwijking om te testen of een populatie een normale verdeling heeft of niet. De formule om te bepalen of een populatie al dan niet normaal verdeeld is, is:
Q1 – (σ z1) + X
Q3 – (σ z3) + X
Waarbij Q1 het eerste kwartiel is, Q3 het derde kwartiel, σ de standaardafwijking, z de standaardscore (“z-score”) en X het gemiddelde. Om te bepalen of een populatie normaal verdeeld is, moet men beide vergelijkingen oplossen en vervolgens de resultaten vergelijken. Als er een significant verschil is tussen de resultaten en het eerste of derde kwartiel, dan is de populatie niet normaal verdeeld.
Terug naar boven
Waarvoor wordt een Interkwartielafstand gebruikt?
De IQR wordt gebruikt om te meten hoe ver de datapunten in een reeks van het gemiddelde van de dataset afliggen. Hoe hoger de IQR, hoe meer de gegevenspunten uit elkaar liggen; hoe kleiner de IQR, hoe dichter de gegevenspunten bij het gemiddelde liggen. Het IQR-bereik is een van de vele metingen die worden gebruikt om te meten hoe gespreid de gegevenspunten in een gegevensreeks zijn. Het wordt het best gebruikt in combinatie met andere metingen, zoals de mediaan en het totale bereik, om een compleet beeld te krijgen van de neiging van een gegevensverzameling om zich rond het gemiddelde te concentreren.
Terug naar boven
Waar komt de term Interkwartielafstand vandaan?
Wie heeft de term “Interkwartielafstand” uitgevonden? Om daar achter te komen, moeten we terug naar de 19e eeuw.
Geschiedenis
De Britse arts Sir Donald MacAlister gebruikte de termen lower quartile en higher quartile in de publicatie uit 1879, the Law of the Geometric Mean. Proc. R. Soc. XXIX, p. 374: “Aangezien deze twee maten, met het gemiddelde, de curve van de faciliteit in vier gelijke delen verdelen, stel ik voor ze respectievelijk het ‘hogere kwartiel’ en het ‘lagere kwartiel’ te noemen.”
Hoewel hij van beroep arts was, was hij begaafd met wiskunde en behaalde hij in 1877 de hoogste score in het eindexamen wiskunde aan de universiteit van Cambridge. Hij sprak negentien talen, waaronder Engels, Tsjechisch en Zweeds.
Macalister’s artikel, de wet van het meetkundig gemiddelde, was eigenlijk een antwoord op een vraag van Francis Galton (uitvinder van het Galtonbord). Maar pas in 1882 gebruikte Galton (“Report of the Anthropometric Committee”) de waarden bovenkwartiel en onderkwartiel en de term “interkwartiel bereik” – gedefinieerd als twee keer de waarschijnlijke fout. Galton was niet alleen een statisticus, hij was ook een antropoloog, geograaf, proto-geneticus en psychometricus die meer dan 340 boeken heeft geproduceerd. Hij bedacht ook de statistische termen “correlatie” en “regressie naar het gemiddelde.”
Gonick, L. en Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, pp. 20-21, 1993.
Stephanie Glen. “Interkwartielafstand (IQR): Wat het is en hoe het te vinden” Van StatisticsHowTo.com: Elementaire Statistiek voor de rest van ons! https://www.statisticshowto.com/probability-and-statistics/interquartile-range/
——————————————————————————
Heb je hulp nodig bij een huiswerk of toetsvraag? Met Chegg Study kunt u stap-voor-stap oplossingen voor uw vragen krijgen van een expert op dit gebied. Uw eerste 30 minuten met een Chegg-leraar zijn gratis!