

In het jaar 1072 AD, documenteerde Omar Khayyam de meest nauwkeurige jaarlengte ooit berekend – een cijfer dat nog steeds nauwkeurig genoeg is voor de meeste doeleinden in de moderne wereld. Khayyam was een astronoom, astroloog, arts, filosoof en wiskundige: hij leverde uitstekende bijdragen op het gebied van de algebra. Zijn poëzie is in het Westen bekender dan die van welke andere niet-Westerse dichter ook.
De man zelf blijft een raadsel. Verschillende biografen hebben hem beschreven als een vrolijke, wijndrinkende agnost; een verstokte Zoroastr; een soefi-moslim; een orthodoxe soennitische moslim; en een aanhanger van de oude Griekse filosofie. Allen zijn het erover eens dat hij een uitmuntend intellectueel was.
Begin
Omar Khayyam werd op 18 mei 1048 geboren in de grote handelsstad Nishapur in het noorden van Perzië. Tegenwoordig ligt de stad in Iran. Omar’s vader was Ebrahim Khayyami, een rijke arts. De naam van Omar’s moeder is niet bekend. Sommige auteurs hebben geschreven dat Omar’s vader de kost verdiende met het maken van tenten, omdat Khayyami tentenmaker betekent. Maar hoewel veel Engelssprekenden Smith heten, betekent dat niet dat hun vaders hun dagen doorbrachten met het hameren van heet metaal op een aambeeld.
Omar’s familie was Moslim. Zijn vader schijnt zich ontspannen te hebben opgesteld ten opzichte van het geloof en nam een wiskundige in dienst met de naam Bahmanyar bin Marzban, een aanhanger van de oude Perzische religie van het Zoroastrisme, om Omar bij te scholen. Bahmanyar was een leerling geweest van de grote arts, wetenschapper en filosoof Avicenna, en hij gaf Omar een grondige opleiding in wetenschap, filosofie en wiskunde. Khawjah al-Anbari leerde Omar astronomie en leidde hem door de Almagest van Ptolemaeus.
In zijn vroege tienerjaren werkte Omar in de chirurgie van zijn vader en leerde hij over de geneeskunde.
Omar Khayyam vierde zijn achttiende verjaardag in 1066. In datzelfde jaar verscheen de komeet van Halley aan de hemel, viel het Normandische leger van Willem de Veroveraar Engeland binnen, en stierf Omar’s vader Ebrahim. Een paar maanden na de dood van Ebrahim stierf ook Omar’s leermeester Bahmanyar.
Het was het einde van een tijdperk in Omar Khayyam’s leven. Het was tijd om orde op zaken te stellen in zijn familie en verder te gaan.
Samarkand
Omar Khayyam sloot zich aan bij een van de regelmatige karavanen die een drie maanden durende reis maakten van Nishapur naar de grote stad Samarkand, die nu in Oezbekistan ligt. Samarkand was een centrum van geleerdheid, en Khayyam arriveerde daar waarschijnlijk in 1068, 20 jaar oud.
In Samarkand maakte hij contact met de oude vriend van zijn vader, Abu Tahir, die gouverneur en opperrechter van de stad was. Tahir, die Khayyams buitengewone talent met getallen opmerkte, gaf hem een baan op zijn kantoor. Al snel kreeg Khayyam een baan in de schatkist van de koning.
Terwijl Khayyam in Samarkand woonde, boekte hij een grote vooruitgang in de algebra.
De bijdragen van Omar Khayyam aan de wetenschap
Algebra
Op de middelbare school leren we over vergelijkingen van de vorm ax2 + bx + c = 0; deze worden kwadratische vergelijkingen genoemd. Kubische vergelijkingen zijn van de vorm ax3 + bx2 + cx + d = 0. Uiteraard zijn kubische vergelijkingen moeilijker op te lossen dan kwadratische.
Khayyam vermoedde terecht dat het niet mogelijk is kubische vergelijkingen op te lossen met de traditionele Oudgriekse meetkundige hulpmiddelen, namelijk passer en liniaal. Er zijn andere methoden nodig.
Op 22-jarige leeftijd, in 1070, publiceerde Khayyam een van zijn grootste werken: Verhandeling over Demonstratie van Problemen van Algebra en Evenwicht. Daarin toonde hij aan dat een kubische vergelijking meer dan één oplossing kan hebben. Hij liet ook zien hoe de snijpunten van kegelsneden zoals parabolen en cirkels kunnen worden gebruikt om meetkundige oplossingen van kubische vergelijkingen te verkrijgen. Archimedes was meer dan duizend jaar eerder op dit gebied begonnen, toen hij het specifieke probleem onderzocht van de verhouding van het volume van het ene deel van een bol tot het andere. Khayyam beschouwde het probleem op een meer algemene, methodische manier.
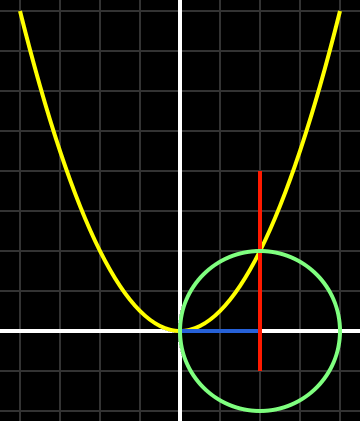
In de taal van de moderne wiskunde bestaat Khayyams oplossing voor de vergelijking x3 + a2x = b uit een parabool met vergelijking x2 = ay, een cirkel met diameter b/a2, en een verticale lijn door het snijpunt. De oplossing wordt gegeven door de afstand op de x-as tussen de oorsprong en de (rode) verticale lijn. Afbeelding door Pieter Kuiper.
Khayyams oplossingen vermeden negatieve coëfficiënten en negatieve wortels omdat negatieve getallen niet erkend werden in de islamitische wiskunde. (Sommige culturen hadden echter wel negatieve getallen in de wiskunde opgenomen – Brahmagupta had bijvoorbeeld 400 jaar eerder negatieve getallen in de Indiase wiskunde geïntroduceerd.)
Hoewel Khayyam’s prestatie magnifiek was, was hij persoonlijk teleurgesteld dat hij meetkunde moest gebruiken om kubische vergelijkingen op te lossen – hij had gehoopt een algoritme te ontdekken met alleen algebra.
Treatise on Demonstration of Problems of Algebra and Balancing vestigde Khayyam als een wiskundige van de eerste rang, en zijn reputatie verspreidde zich snel door heel Perzië.
Na Khayyams doorbraak was er weinig vooruitgang van betekenis op het gebied van kubische vergelijkingen tot 1535, toen Niccolo Tartaglia algemene oplossingen vond voor alle kubische vergelijkingen.
De algebra van Khayyam was niet het systeem van letters en tekens dat wij vandaag de dag gebruiken. Zijn algebra werd uitgedrukt in woorden. Dus, waar we tegenwoordig schrijven:
Oplos voor x:
x2 + 6 = 5x
Khayyam schreef: Wat is de hoeveelheid van een vierkant zodat wanneer er 6 dirhams bij opgeteld worden, het gelijk wordt aan vijf wortels van dat vierkant?
Algebra en Meetkunde koppelen
Algebra en Meetkunde werden in de jaren 1600 met succes aan elkaar gekoppeld door Pierre de Fermat en René Descartes, wat resulteerde in het moderne x-y coördinatenstelsel.
Khayyams werk met kubieken had hem er zeker van gemaakt dat algebra en meetkunde met elkaar verbonden waren, en hij citeerde Euclides’ Elementen om het idee te ondersteunen:
Wie denkt dat algebra een truc is om onbekenden te verkrijgen, heeft het tevergeefs gedacht. Er moet geen aandacht worden besteed aan het feit dat algebra en meetkunde verschillend zijn in verschijningsvorm. Algebra’s zijn meetkundige feiten die worden bewezen door Stellingen 5 en 6 van Boek 2 van Euclides’ Elementen.
Lengte van het jaar
In 1073 ontving Khayyam een uitnodiging om in de Perzische stad Isfahan, hoofdstad van het Seltsjoekse Rijk, een kalender op te stellen die ordelijk zou werken en voor altijd nauwkeurig zou zijn – dit was een tijdperk waarin de jaarlengtes regelmatig werden gewijzigd.
Khayyams uitnodiging kwam van de twee machtigste mannen in het Seldjoekse Rijk, waar Perzië deel van uitmaakte: dit waren Malik Shah, sultan van het rijk, en Nizam al-Mulk, zijn vizier.
Khayyam ronselde andere getalenteerde wetenschappers om hem in 1074 naar Isfahan te vergezellen. Daar kreeg hij een buitengewoon hoog salaris en genoot hij van een bevoorrechte levensstijl. Malik Shah betaalde Khayyam om een observatorium op te richten met als aanvankelijk doel om gedurende 30 jaar waarnemingen aan de hemel te doen, waarbij Saturnus, de meest verre planeet die toen bekend was, een baan zou voltooien.
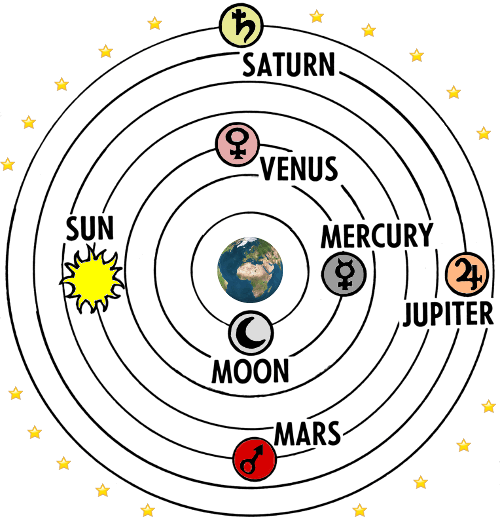
Ptolemaeus’ heelal – het model dat door Omar Khayyam werd aanvaard.
Tijdens zijn verblijf in Isfahan mat Khayyam de lengte van een jaar – om precies te zijn de tropische jaarlengte – met opmerkelijke nauwkeurigheid en precisie.
Khayyam ontdekte dat 1.029.983 dagen samen 2.820 jaar vormen. Dit geeft een tropische jaarlengte van 365,2422 dagen tot zeven significante cijfers. Hoewel het modieus is geworden om meer decimalen dan dit te noemen, bevat Khayyams invoer van 1.029.983 dagen zeven significante cijfers, zodat het onredelijk is om meer dan dit aantal significante cijfers te noemen in de berekende jaarlengte.
Heden ten dage weten we dat de lengte van een tropisch jaar in feite van jaar tot jaar met wel 30 minuten verandert. De gemiddelde tropische jaarlengte die tegenwoordig wordt genoemd is 365,242189 dagen, wat tot zeven significante cijfers 365,2422 dagen is – precies het getal waar Khayyam bijna duizend jaar geleden op uitkwam. De lengte van een tropisch jaar neemt met het verstrijken van de tijd ook iets toe, hoewel niet genoeg tussen Khayyams tijdperk en het onze om merkbaar te zijn op een schaal van zeven significante cijfers.
Malik Shah voerde Khayyams nieuwe kalender op 15 maart 1079 in het Seldjoekse Rijk in. Hij werd tot in de 20e eeuw gebruikt.
Het parallelle postulaat
De 13 boeken van Euclides’ Elementen die rond 300 v.Chr. werden gepubliceerd, waren waarschijnlijk de invloedrijkste boeken in de hele geschiedenis van de wiskunde. De Elementen waren gebaseerd op vijf meetkundige postulaten – met andere woorden vijf dingen waarvan werd aangenomen dat ze waar waren in de meetkunde: bijvoorbeeld dat alle rechte hoeken gelijk zijn aan elkaar.
Het vijfde van Euclides’ vijf postulaten was het parallellenpostulaat. Het parallellenpostulaat bleek millennia lang een bron van raadselachtigheid, ergernis en vreugde voor wiskundigen te zijn. De vreugde was meestal van korte duur voor wiskundigen die dachten dat zij het postulaat hadden bewezen, om vervolgens teleurgesteld te worden wanneer een fout in hun ‘bewijs’ werd ontdekt.
Euclides had zich gebogen over een rechte lijn die twee andere rechte lijnen kruist. Hij keek naar de situatie waarin de binnenhoeken (in de afbeelding hieronder) minder dan 180 graden bedragen. In deze omstandigheden, zei hij, zullen de twee rechte lijnen elkaar uiteindelijk ontmoeten aan de kant van de twee hoeken die optellen tot minder dan 180 graden.
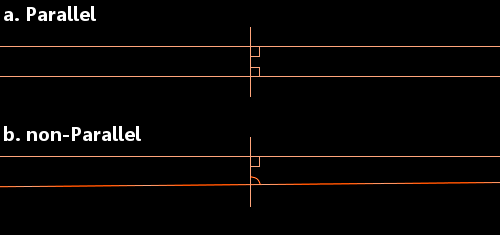
a. Als elke hoek 90 graden is, zijn de lijnen evenwijdig.
b. Als een of beide hoeken kleiner zijn dan 90 graden, zullen de lijnen elkaar snijden.
Sinds de tijd dat Elements voor het eerst werd gepubliceerd, hadden wiskundigen geprobeerd Euclides’ eerste vier postulaten te gebruiken om het parallellenpostulaat te bewijzen. Ze waren gedoemd te mislukken. We weten nu dat het onmogelijk is om het parallellenpostulaat te bewijzen met behulp van Euclides andere postulaten.
De poging van Omar Khayyam was interessant. In zijn Explanations of the Difficulties in the Postulates in Euclid’s Elements vraagt hij zijn lezers een rechte lijn AB te beschouwen:


Hij vraagt zijn lezers twee gelijke lijnen te beschouwen die loodrecht op AB staan en ziet drie mogelijke rangschikkingen, die vierzijdige figuren kunnen opleveren:
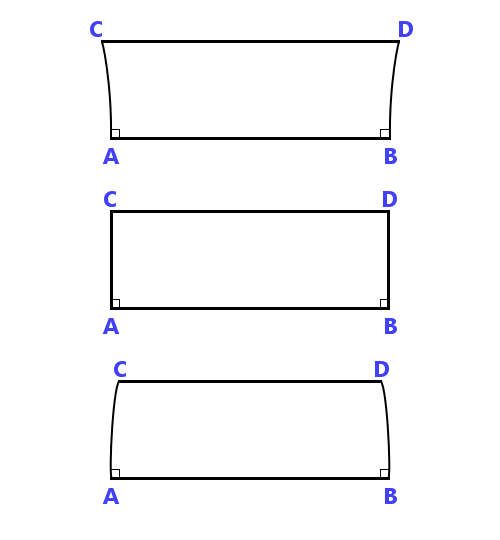

Hij weerlegt vervolgens de mogelijkheid dat hoeken C en/of D iets anders dan rechte hoeken kunnen zijn en in de bovenstaande afbeelding is alleen de middelste optie mogelijk. Hij denkt dus dat hij het parallellenpostulaat heeft bewezen. In feite heeft hij dat niet gedaan, hij heeft het alleen op een andere manier geformuleerd.
Wat interessant is voor historici van de wiskunde is dat zij in Khayyams ideeën – ruwweg weergegeven in de afbeeldingen hierboven – de eerste glimpen van niet-Euclidische meetkunde kunnen zien.
Enkele persoonlijke details en het einde
Volledige details van Khayyams persoonlijke leven zijn niet bekend. Aangenomen wordt dat hij getrouwd is geweest en minstens één zoon en één dochter had.
In 1092 stierven Malik Shah en zijn vizier – de eerste waarschijnlijk door vergiftiging, de tweede door een moordaanslag. Khayyam dook onder tijdens de daaruit voortvloeiende machtsstrijd. Hij kon alleen overleven door zich gedeisd te houden. Hij was de lijfarts van Malik Shah geweest en was diens persoonlijke vriend geworden – wat hem vijanden had gemaakt – en Khayyam’s poëzie suggereert dat zijn gedrag misschien niet vroom religieus was – en ook dit had hem vijanden gemaakt. Khayyam publiceerde eigenlijk geen poëzie tijdens zijn leven. Sommige van zijn overpeinzingen zouden mogelijk zijn leven in gevaar hebben gebracht.
Na de machtsstrijd duurde het ongeveer 20 jaar voordat Khayyam volledig gerehabiliteerd was en hij op 64-jarige leeftijd weer opdook in het gezelschap van machtige mensen. Hij weigerde echter les te geven. Een van zijn gedichten suggereert waarom dit zou kunnen zijn:
kunnen niet worden verteld uit angst voor verlies van het hoofd;
Sinds niemand geschikt is om te leren, of zich bekommert om te weten,
Het is beter dat al mijn gedachten ongezegd blijven.
Omar Khayyam stierf op 83-jarige leeftijd in zijn geboorteplaats Nishapur op 4 december 1131. Hij werd begraven in een tombe die hij zelf had uitgekozen in een boomgaard waar tweemaal per jaar bloesem zou vallen.
De poëzie van Khayyam werd in de jaren 1800 populair gemaakt door de vertalingen van Edward FitzGerald in de Rubaiyat van Omar Khayyam. Khayyam werd in het Westen zo bewonderd dat de Sjah van Iran in 1963 zijn graf liet opgraven en Khayyams stoffelijke resten liet overbrengen naar een enorm, speciaal voor dat doel gebouwd mausoleum in Nishapur, waar toeristen hulde konden brengen aan de grote dichter.
We eindigen met een van Khayyams beroemdste en meest tot de verbeelding sprekende kwatrijnen:
Een Kruik Wijn, een Brood-en Gij
Bij mij zingend in de Wildernis-
En de Wildernis is het Paradijs genoeg.”
Auteur van deze pagina: The Doc
Foto’s digitaal verbeterd en ingekleurd door deze website. © Alle rechten voorbehouden.
Citeer deze pagina
Gebruik de volgende MLA-conforme citatie:
"Omar Khayyam." Famous Scientists. famousscientists.org. 5 Nov. 2016. Web. <www.famousscientists.org/omar-khayyam/>.
Gepubliceerd door FamousScientists.org
Verder Lezen
Edward FitzGerald (vertaler)
The Rubaiyat of Omar Khayyam
Howard Willford Bell, 1901
Victor J. Katz
A History of Mathematics: An Introduction
HarperCollins College Publishers, New York, 1993
Roshdi Rashed (Editor)
Encyclopedia of the History of Arabic science
Routledge, 1996
History of Astronomy – Middle East
ephemeris.com, 2003
Hazhir Teimourian
Omar Khayyam: Dichter, Rebel, Astronoom
The History Press, 2008
Mehdi Aminrazavi
De Wijn der Wijsheid: Het leven, de poëzie en de filosofie van Omar Khayyam
Oneworld Publications, 2013